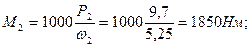Порядок решения задачи №2.

К решению этой задачи следует приступить после изучения тем:

- Понятие о сложном деформированном состоянии

- Понятие о теориях прочности

- Расчет вала на изгиб и кручение

Пример 2

На рис.2 на вал насажены три зубчатых колеса. Зубчатые колеса нагружены силами: F₁=2кН; F₂=1,5кН; F₃=1,2кН; причем силами F₁ и F₂ направлены горизонтально, а сила F₃ – вертикально.

Диаметры колес: D₁=300 мм; D₂=200 мм; D₃=250 мм.

Построить эпюру крутящих моментов М_к и эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях, пренебрегая массой колес и самого вала. Определить требуемый диаметр вала по третьей теории прочности. Допустимое напряжение [σ] = 50 мПа

рис.2

 

 

Решение

1. Вычисляем внешние моменты от силы F₁; F₂; и F₃, скручивающих вал:

;

 

1. На участке II проводим сечение а-а и получаем:

М_КII=-М₂= -150Нм; знак минус показывает, что внешний момент приложенной к левой части, вращает ее против часовой стрелки, если смотреть со стороны сечения.

 

1. На участке III проводим сечение в-в и рассматриваем правую отсеченную часть: М_Кш= М₃= 150Нм

левая отсеченная часть представляется

М_Кш = -М₂ + М₁= -150 + 300 = 150 Нм;

 

1. В поперечных сечениях участков I и III крутящие моменты равны нулю (трением подшипников пренебрегаем).

 

1. По результатам расчетов строим эпюру крутящих моментов на рис.2б.
2. Сила F₃ вызывает изгиб в вертикальной плоскости. Покажем изгибающую нагрузку на рис.2в.
3. Определяем опорные реакции R_A и R_В:

∑М_А=0; F₃(а+в+с) – R_B(а+в+с+d)=0

∑F_iy=0; -F₃ + R_B + R_A=0

откуда

R_A=F₃ – R_B= 240 Н.

 

1. Определяем ординаты эпюры изгибающих моментов в вертикальной плоскости:

- в сечении А М_А^В=0

- в сечении С М_С^В= R_A^B*a = 240*0,3 = 72 Нм

- в сечении D М_D^В= R_A^B(a+b) = 240*0,7 = 168 Нм

- в сечении E М_E^В= R_B^B*d = 960*0,3 = 288 Нм

 

1. На рис.2г строим эпюру изгибающих моментов в вертикальной плоскости.
2. Определяем горизонтальные составляющие опорных реакций от нагружения вала горизонтальными силами F₁ и F₂ на рис.2д.

отсюда

∑М_А=0; F₂*а – R₁(а+b) + R_B^Г(а+b+c+d)=0

∑F_ix=0; -R_A^Г + F₂ – F₁ +R_В^Г=0

определяем:

R_A^Г= - F₁+F₂ + R_B^Г = 133Н

 

1. Определяем ординаты эпюры моментов в горизонтальной плоскости:

- в сечении А М_А^Г=0

- в сечении С М_С^Г= R_A^Г*a = 133*0,3 = 40 Нм

- в сечении D М_D^Г= R_A^Г(a+b) – F₂b= 133*0,7 – 1500*0,4 =

=-507 Нм

- в сечении E М_E^Г= R_B*d = -633*0,3 = -190 Нм

- в сечении В М_В^Г =0

12. Строим эпюру моментов в горизонтальной плоскости на рис.2е

 

13. Так как изгибающие моменты М^В и М^Г работают в перпендикулярных плоскостях, то суммарный изгибающий момент определяется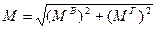

Найдем наибольший суммарный изгибающий момент в сечении D.

Сечение D является самым опасным т.к. здесь самая большая нагрузка.

 

14. По третьей теории прочности определяем момент сопротивления сечения вала

 

15. Вычисляем диаметр вала, пологая что W≈ 0,1d³

Порядок решения задачи №3

К выполнению третьей задачи следует приступить после изучения тем:

- Классификация передач и их назначение

- Кинематические и силовые соотношения в передаточных механизмах.

Пример 3

Определить моменты и мощности на каждом из валов двухступенчатой передачи изображенной на рисунке 3, учитывая, что КПД каждой передачи ŋ=0,98; КПД учитывающий потери в опорах одного вала ŋ_оп=0,99; Полезная мощность на первом валу Р₁=10 кВт, частота вращения первого вала n₁=100 об/мин; передаточные отношения i₁₂=2; i₂₃=2,5

 

Решение

1. Определяем угловые скорости и частоты вращения валов:

n₁=100 об/мин;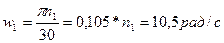

 

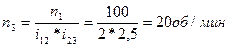
1. Определяем КПД от первого вала ко второму и третьему:

Ŋ₁₂=0,99*0,98=0,97; ŋ₁₃=0,99²*0,98²=0,958;

 

1. определяем мощности подводимые ко второму и третьему валам:

Р₂=Р₁* ŋ₁₂= 10*0,97 = 9,7 кВт;

Р₃= Р₁* ŋ₁₃= 10*0,958 = 9,58 кВт;

1. Определяем моменты на валах: