Порядок решения задачи №4

К решению данной задачи следует приступить после проработки и усвоения тем:

1. «Основные допущения и гипотезы»
2. «Метод сечений и виды деформаций»
3. «Напряжения»
4. «Продольные силы при растяжении и сжатии»
5. «Построение эпюр продольных сил»

Пример 4

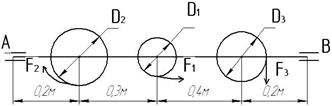
Стержень закреплен одним концом и нагружен приложенными вдоль оси силами F₁; F₂ и F₃ (рис.5). Построить для этого стержня эпюру продольных сил.

 

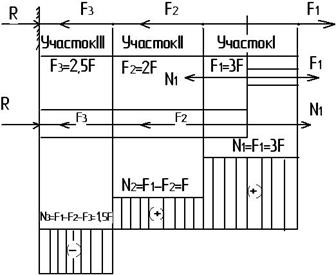
Рис.5

Решение

1. В защемленном сечении возникает реакция R, которую можно определить из уравнения равновесия:

∑F_iz=0 R-F₃-F₂+F₁=0; откуда R=F₃+F₂-F₁

1. Разделим стержень на участки I, II и III и пользуясь методом сечений, определим продольные силы на каждом участке. Проведем сечение на участке I и рассмотрим правую отсеченную часть стержня (рис.5) при этом:

N₁=F_1;

1. Рассмотрим левую отсеченную часть стержня, найдем: N₁=F₂+F₃-R;

но из условия R=F₃+F₂-F₁

1. Подставим значение R в выражение продольной силы, для первой части стержня, получим:

N₁=F₂+F₃-R=F₂+F₃-F₃-F₂+F₁=F₁

1. Аналогично проведем сечение в пределах II-го и III-го участков и найдем:

N₂=F₁-F₂; N₃=F₁-F₂-F₃

1. Строим эпюру продольных сил на рис.5. по значениям N на каждом участке.

 

Контрольная работа №2

Задача №1

 

Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рисунке. Данные для построения взять из таблицы №1.

 

Таблица № 3

ВАРИАНТ
№ схемы		6

 

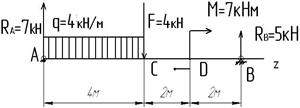
1.

 

 

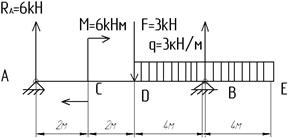
2.

 

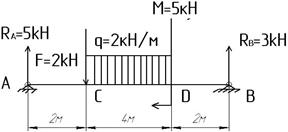
3.

 

 

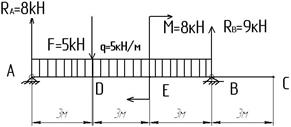4.

 

 

5.

 

 

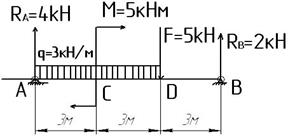
6.

 

 

Задача №2

Построить эпюру крутящих моментов М_к и эпюры изгибающих моментов в вертикальной и горизонтальных плоскостях, пренебрегая массой колес и самого вала. Определить требуемый диаметр вала третьей теории прочности. Допускаемое напряжение [σ]=50МПа. Данные для решения взять из таблицы №2.

 

 

Таблица № 2

ВАРИАНТ
схема
F1 (кН)	0,5	0,8	1,0	1,2	1,4	1,6	1,7	1,8	1,9	2,0
F2 (кН)	0,6	0,7	0,8	0,9	1,0	1,1	1,2	1,3	1,4	1,5
F3 (кН)	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2	1,3
D1 (мм)
D2 (мм)
D3 (мм)

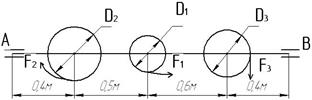
1.

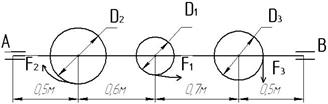
2.

 

 

 

3.

 

4.

 

 

5.

 

Задача №3

Определить моменты и мощности на каждом из валов двухступенчатой передачи изображенной на рисунке 3. Данные для решения задачи взять из таблицы 3.

Таблица № 3

ВАРИАНТ
КПД передачи (η)	0,98	0,97	0,96	0,95	0,96	0,97	0,98	0,95	0,96	0,97
КПД в опорах (ηоп)	0,99	0,98	0,97	0,98	0,99	0,97	0,99	0,98	0,97	0,99
Мощность на I валу (Р1) кВт
Частота вращения первого вала (n1) (об/мин)
Передаточные отношения (i12)
Передаточные отношения (i23)	1,5		2,5		3,5		4,5		1,5

 

 

 

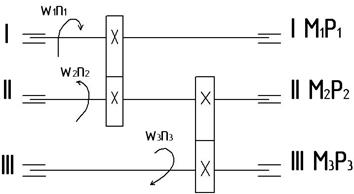
Рис.3

Задача №4

Описать устройство, достоинства, недостатки, классификацию, область применения передачи. Данные взять из таблицы 4.

 

Таблица № 4

ВАРИАНТ
Задание	Фрикционные передачи	Зубчатые передачи	Цепные передачи	Ременные передачи	Червячные передачи	Фрикционные передачи	Зубчатые передачи	Цепные передачи	Ременные передачи	Червячные передачи

 

 

Методические указания по выполнению

Контрольной работы №2

К выполнению первой задачи следует приступить после проработки и усвоения тем:

- «Основные понятия»

- Поперечные силы и изгибающие5 моменты в сечениях балок»

- «Эпюры поперечных сил и изгибающих моментов»

- «Построение эпюр поперечных сил и изгибающих моментов по характерным точкам».

- «Расчеты на прочность при изгибе».

- «Нормальные напряжения при изгибе».

 

Порядок решения задачи №1

Пример 1

Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис.1.

 

 

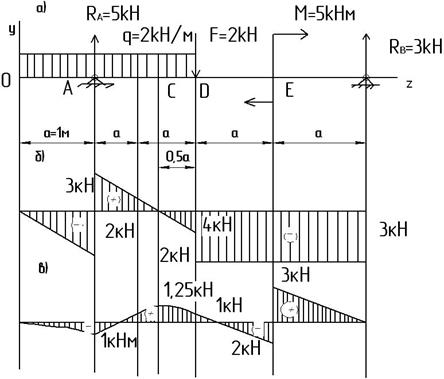
Рис.1

Решение

1. Определяем опорные реакции:

∑М_A=0; q*3а*0,5а + F*2а + М – R_B*4a = 2*3*0,5 + +2*2+5-R_B*4=0

∑M_B=0; -q*3a*3,5*a +R_A*4a – FR*2a +M = -2*3*3,5+ +R_a*4 – 2*2 +5 =0

откуда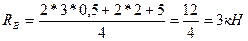

 

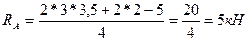
1. Для проверки правильности определения опорных реакций составляем сумму проекций всех сил, приложенных к балке на вертикальную ось у:

∑F_iy=0; -q*3a + R_A – F + R_B=0;

-2*3 + 5 – 2 + 3=0

Значит опорные реакции найдены верно.

 

1. Характерные точки на балке: А; В; Д; Е;О вычислим значение поперечных сил в сечениях, проходящих через данные точки.

- в сечении О Q=0;

- в сечении А слева Q_А^лев= - q*а = -2кН

- в сечении А справа Q_A^прав= -q*a + R_A = -2 + 5 = 3кН

- в сечении D слева Q_D^лев= - 3q*a + R_A= -3*2 + 5 = -1 кН

- в сечении D справа Q_D^прав= - 3q*a +R_A -F= -3*2 +5- 2 =-3кН

В сечении В поперечная сил отрицательна и численно равна: R_B=3кН.

 

4. По найденным числовым значениям строим эпюру поперечных сил (рис.1а)

Поперечная сила в точке С принимает значение Q=0 и сечение в точке С имеет максимальное значение изгибающего момента, из подобия треугольников, выводим, что СD=0,5а.

5.Производим расчет изгибающих моментов в характерных точках: из условий ОМ=0

– в сечении А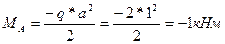

- в сечении С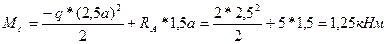

- в сечении D M_D=-q*3a*1,5a+R_A*2a =-2*3*1,5+5*2= 1кНм

- в сечении Е (место приложения пары сил) вычисляем моменты слева и справа – от пары сил.

- в сечении Е слева М_Е^лев= -q*3a*2,5a + R_A*3a – F_a=

= -2*3*2,5 + 5*3 – 2*1 = -2 кНм

- в сечении Е справа М_Е^прав = М_Е^лев + М = -2 + 5 = 3 кНм

- в сечении В М_В=0.

 

6. Производим построение эпюры изгибающих моментов (рис.1в) исходя из видов уравнений, на участке ОЕ эпюра изображается параболой и на участке ЕВ – в виде прямых наклонных линий.