Геометрические приложения производной

Дифференциальное исчисление

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

и варианты расчетно–графических работ

для подготовки бакалавра по направлениям

080100 Экономика

Экономика предприятий и организаций

Бухгалтерский учет, анализ и аудит

Финансы и кредит

Налоги и налогообложение

Уфа 2012

УДК 517.2

ББК 161.6

М 54

Методические указания

Обсуждены и одобрены на заседании кафедры математики

(протокол № от)

Заведующий кафедрой математики, к.ф.-м.н., доцент Лукманов Р.Л.

Рекомендовано к изданию методической комиссией механического факультета (протокол № от)

Председатель методической комиссии факультета к.пс.н., доцент Костенко Н.А.

Составители: к.ф.-м.н., доцент Кудашева Е.Г.,

к.ф.-м.н., доцент Чередникова Л.Ю.

Рецензент: к.эк.н., доцент Насырова А.Д.

Ответственный за выпуск: заведующий кафедрой математики,

к.ф.-м.н., доцент Лукманов Р.Л.

Введение

Залог успешного овладения курсом математики – активная самостоятельная работа студентов. Одна из форм активизации учебного процесса – система расчетно-графических работ (РГР). Основой системы данной работы является индивидуализация заданий. Данные методические указания предназначены для изучения раздела «Дифференциальное исчисление».

В методическом указании представлены задачи по темам: вычисление производной различных типов функций, нахождение пределов функций с помощью правила Лопиталя, геометрическое приложение производной. В настоящем сборнике представлены тридцать различных вариантов заданий. Варианты заданий выдаются преподавателем.

Определение производной. Дифференцирование функций

Пусть функция у = f (x) определена на промежутке . Аргументу дадим приращение , найдем соответствующее приращение функции .

Производной функции у = f (x) в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю:

Если предел конечный, то производная функции f (x) существует. Функция f, имеющая производную в каждой точке интервала , называется дифференцируемой. Производная обозначается также у' (x)или

Приведем основные правила дифференцирования функций.

Пусть С Î R — постоянная, и = и (х), v = v (x) — функции, имеющие производные.

С ' = 0(Си) ' =С ∙ u'

(u ± v) ' = и' ± v' (u ∙ v) ' =u' ∙ v + u ∙ v'

Дифференцирование сложной функции y = f (φ (x)). Если функция y = f (u) дифференцируема по и, а функция и = φ (x) — по х, то сложная функция

y = f (φ (x)) имеет производную y' =f ' (u) ∙ u' (x).

Таблица производных основных элементарных функций

Производной второго порядка (второй производной) от функции называется производная от ее производной, т. е. .

Вторую производную также обозначают или . Производная от производной второго порядка называется производной третьего порядка и т. д. Производную n -го порядка обозначают или .

Примеры.Используя правила дифференцирования и таблицу производных, найдем производные следующих функций:

1) , 2) , 3) ,

4) , 5) , 6) , 7) .

Решение.1) Перепишем данную функцию, записав слагаемые в виде степени: .

Тогда .

2) Представим данную функцию в виде степени

3) Применив формулу дифференцирования произведения функций, находим:

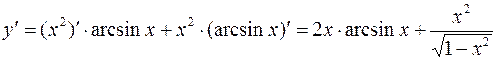4) Дифференцируем функцию как сложную

5) В соответствии с формулой дифференцирования частного получим

6) По аналогии с примером 3 находим:

7) Продифференцируем функцию как показательную

Выведем формулу для нахождения производной степенно–показательной функции , считая что и дифференцируемые функции и .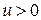

Логарифмируя равенство и дифференцируя обе части полученного равенства , находим:

Следовательно,

Таким образом .

Пример. , где х> 0,

Геометрические приложения производной

Если кривая задана уравнением , то значение производной в точке равно угловому коэффициенту касательной к кривой в точке : , где (рис.1).

Рис. 1.

Уравнение касательной к кривой в точке имеет вид

Углом между двумя кривыми в точке их пересечения называется угол между касательными к кривым в этой точке.

Угол между двумя прямыми с угловыми коэффициентами и находится по формуле:

причем знак “плюс” соответствует острому углу , а знак “минус”— тупому.

Если , то касательные — взаимно перпендикулярны, а кривые называются ортогональными.

Пример. Найти уравнение касательной к графику функции , которая параллельна прямой . Сделать чертеж.

Решение. График функции — парабола. Так как при , , то вершиной параболы является точка (2; –1). По условию, касательная к параболе и данная прямая с уравнением параллельны, следовательно, их угловые коэффициенты равны: