Расчет механической части электропривода
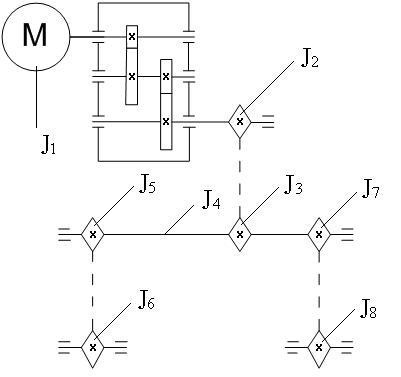
Рис.1. Кинематическая схема ротационного выталкивателя.
Таблица 1. Основные данные для расчета механической части электропривода
Момент инерции мотороредуктора J1, 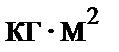
| 0,0021 |
Диаметр звёздочек D2 и D3, 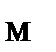
| 0,178 |
Масса звёздочек M2 и M3, 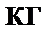
| 7,3 |
Диаметр звёздочек D5 и D7, 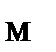
| 0,386 |
Масса звёздочек M5 и M7, 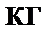
| 27,6 |
Диаметр звёздочек D6 и D8, 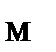
| 0,261 |
Масса звёздочек M6 и M8, 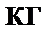
| |
Масса вала Mв, 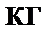
| 36,8 |
Длинна вала Lв, 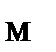
| 1,666 |
Диаметр вала Dв, 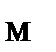
| 0,06 |
| Число зубьев звёздочек z5 и z7 | |
| Число зубьев звёздочек z6 и z8 | |
Длинна цепи Lц1, 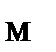
| 0,386 |
Площадь поперечного сечения цепи Sц1, 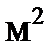
| 0,00173 |
Длинна цепей Lц2 и Lц3, 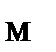
| 1,881 |
Площадь поперечного сечения цепей Sц2 и Sц3, 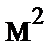
| 0,00237 |
Расчет моментов инерции звёздочек:
 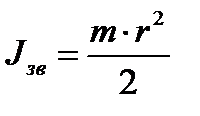 ; ;
| (3.1) |

Расчет момента инерции вала:
 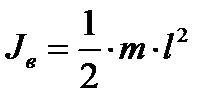 ; ;
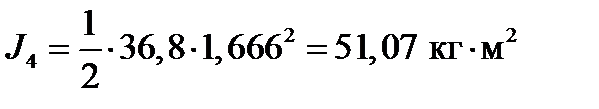
| (3.1) |
Расчет жесткостей цепей:
 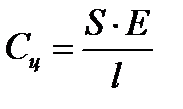 ;
где ;
где 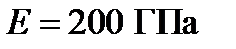 -модуль линейной упругости -модуль линейной упругости
| (3.1) |
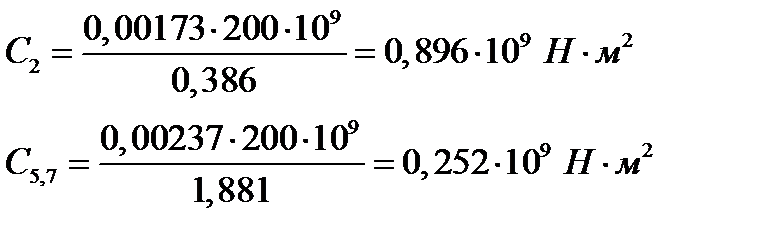
Расчет жесткостей вала:
 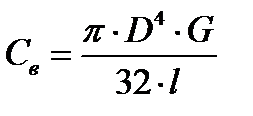 ;
где ;
где 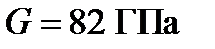 -модуль жесткости при кручении -модуль жесткости при кручении
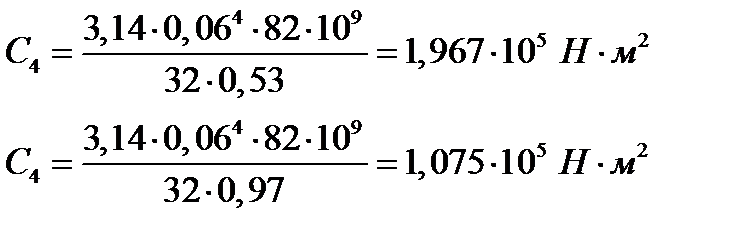
| (3.1) |
Расчет передаточного числа звёздочек:
 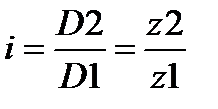 ; ;
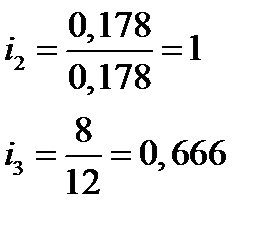
| (3.1) |
Рис.2. Расчетные вращательные схемы механической части электропривода.
Объединение моментов инерции мотороредуктора J1 и звёздочки J2:
 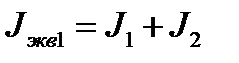 ; ;
| (3.1) |
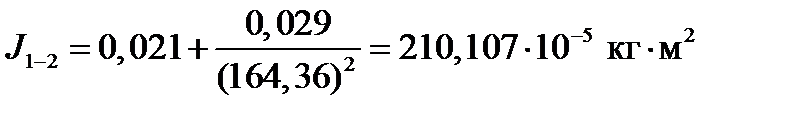
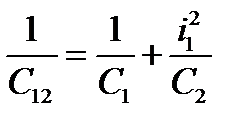
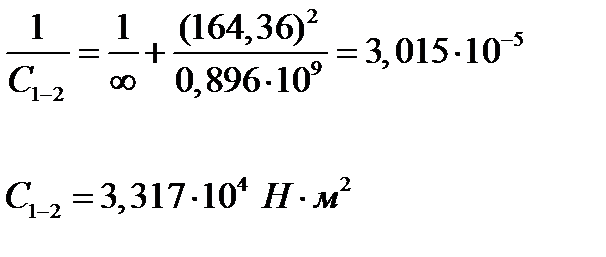 Объединение моментов инерции звёздочки J5 и звёздочки J6:
Объединение моментов инерции звёздочки J5 и звёздочки J6:
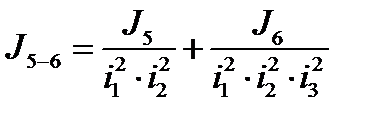
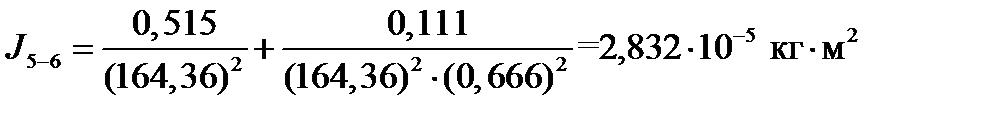
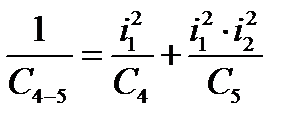
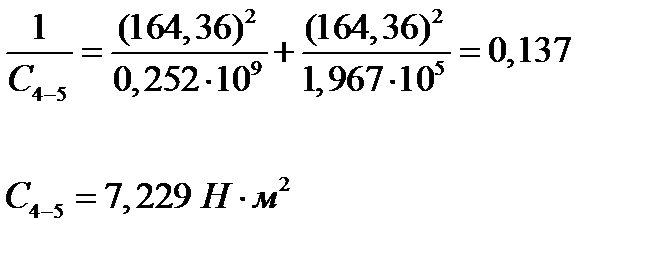 Объединение моментов инерции звёздочки J7 и звёздочки J8:
Объединение моментов инерции звёздочки J7 и звёздочки J8:
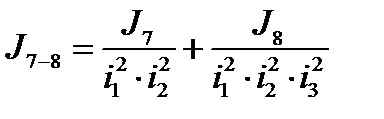
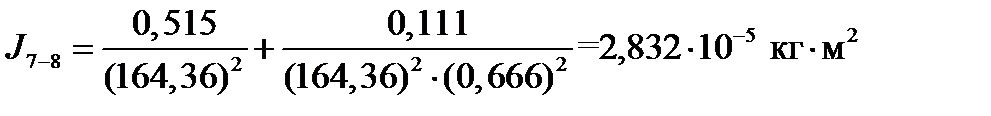
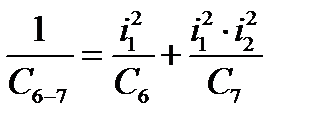
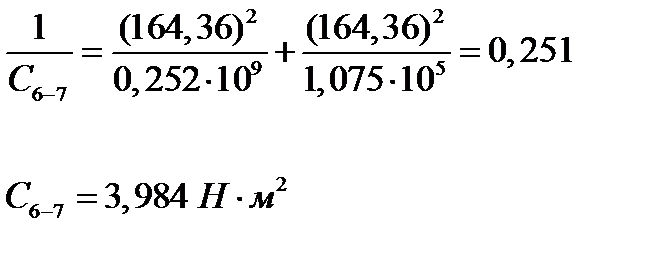 Объединение моментов инерции звёздочки J3 и вала J4:
Объединение моментов инерции звёздочки J3 и вала J4:
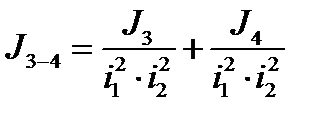
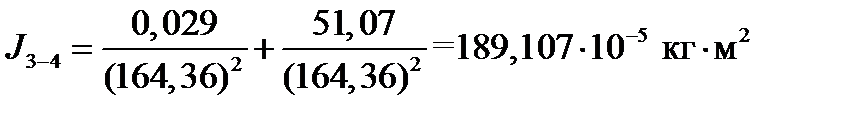
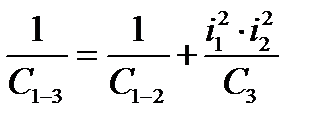
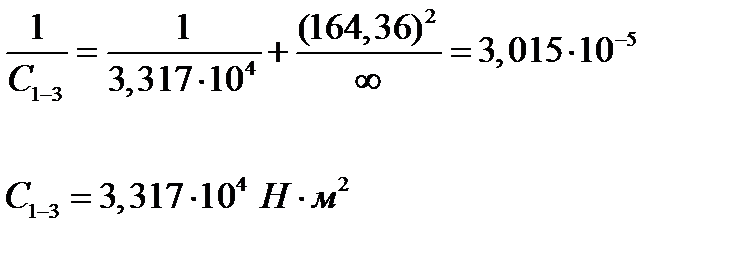 Объединение моментов инерции J3-4 и J7-8:
Объединение моментов инерции J3-4 и J7-8:
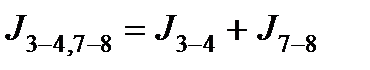
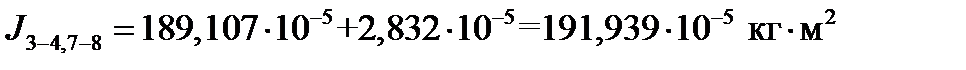
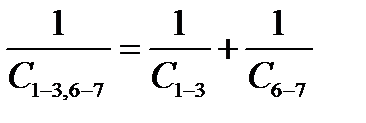
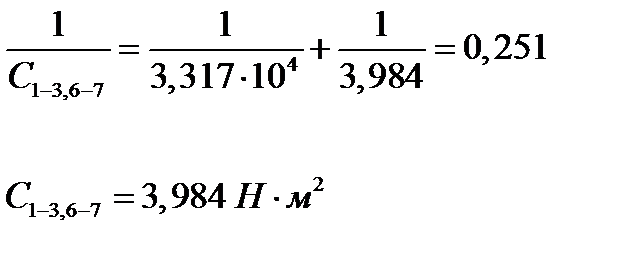
|
Расчет трехмассовой системы
После приведения к трехмассовой системе принимаем:
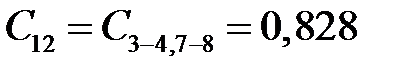 Н∙м2,
Н∙м2, 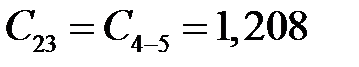 Н∙м2;
Н∙м2;
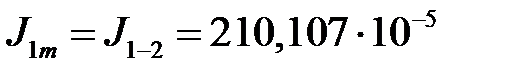 кг∙м2,
кг∙м2, 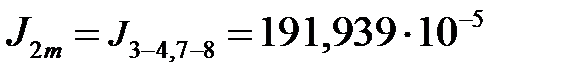 кг∙м2,
кг∙м2, 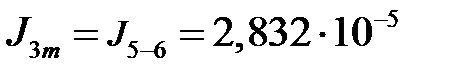 кг∙м2.
кг∙м2.
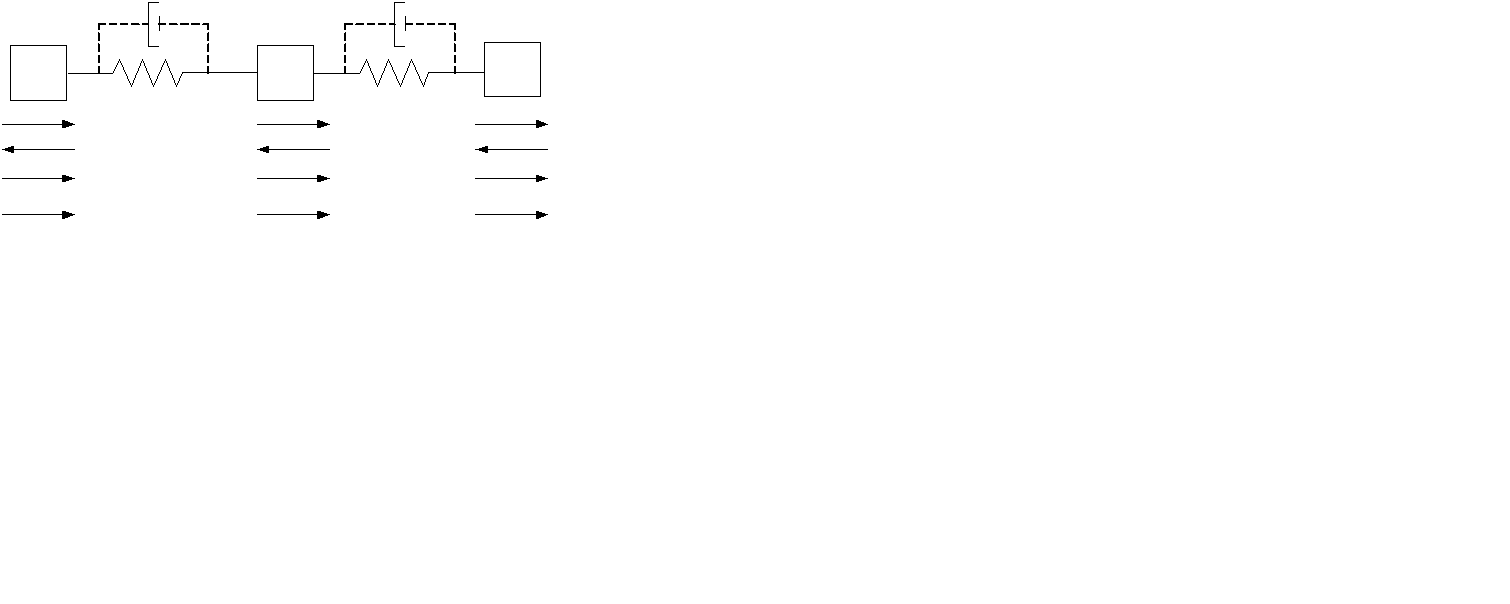
| J1 |
| J2 |
| J3 |
| b12 |
| b23 |
| C12 |
| C23 |
| M |
| M12 |
| j1 |
| w1 |
| M12 |
| M23 |
| j2 |
| w2 |
| M23 |
| Mc |
| j3 |
| w3 |
Рис.2.3. Расчетная схема трехмассовой последовательности упругой системы.
> >
| М |
| Мс1 |
| М12 |
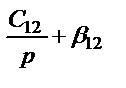
|
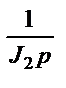
|
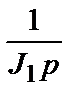
|
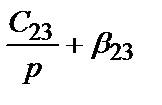
|
| w1 |
| w2 |
| М12 |
| Мс2 |
| М23 |
| w2 |
| w3 |
| М23 |
| Мс3 |
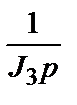
|
| w3 |
Рис.2.4. Структурная схема трехмассовой упругой механической системы.
Решив биквадратное уравнение, получаем корни характеристического уравнения системы:
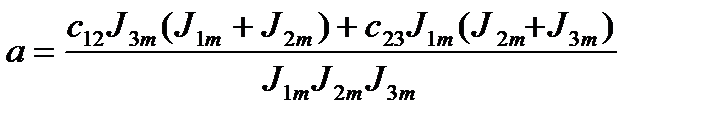 ; (2.10)
; (2.10)
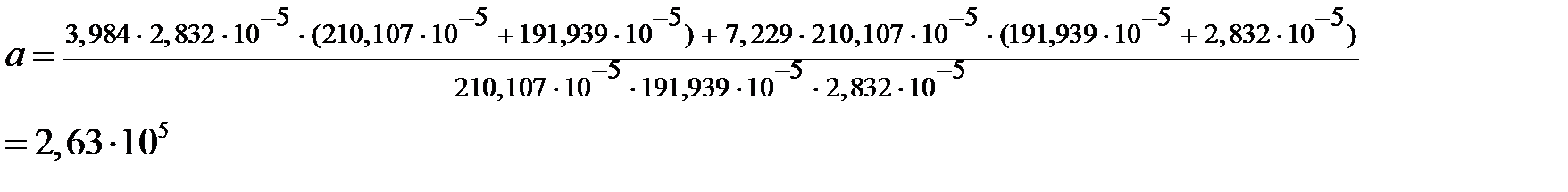
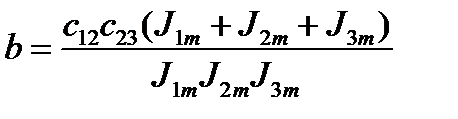 ; (2.11)
; (2.11)
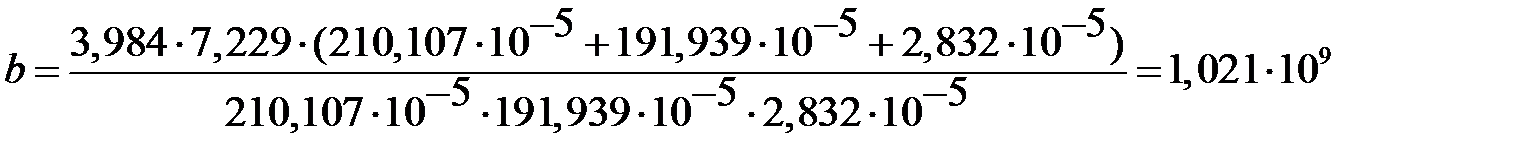
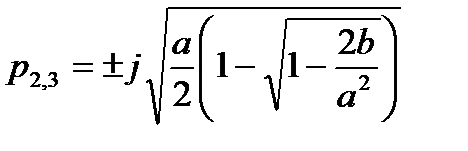 ; (2.12)
; (2.12)
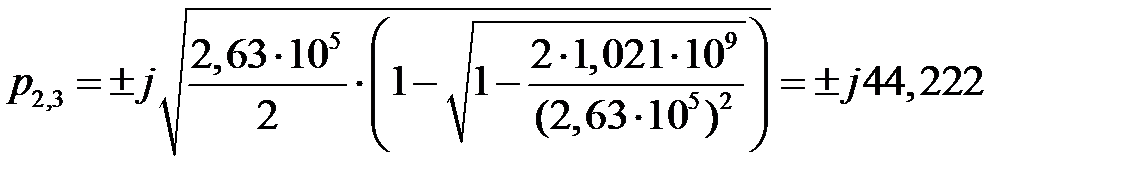
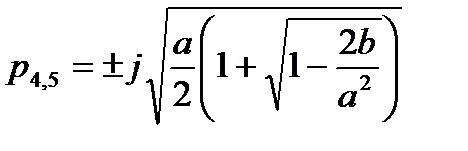 ; (2.13)
; (2.13)
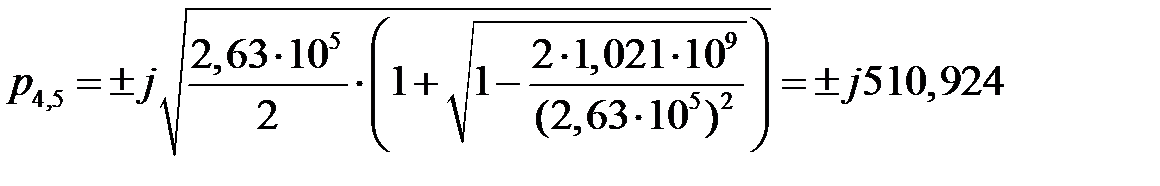
Корни характеристического уравнения свидетельствуют о том, что система может быть представлена в виде последовательного соединения интегрирующего звена и двух консервативных колебательных звеньев с резонансными частотами колебаний 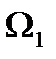 и
и 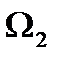 . Следовательно,
. Следовательно,
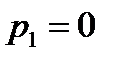 ;
; 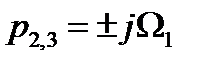
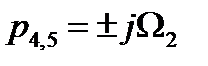
Для расчёта коэффициентов вязкого трения зададимся значением логарифмческого декремента затухания 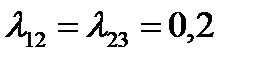 .
.
Коэффициент вязкого трения между первой и второй массами:
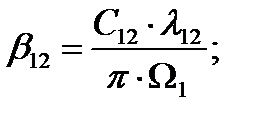 (2.14)
(2.14)
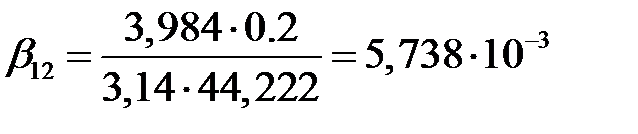
Коэффициент вязкого трения между второй и третьей массами:
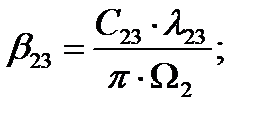 (2.15)
(2.15)
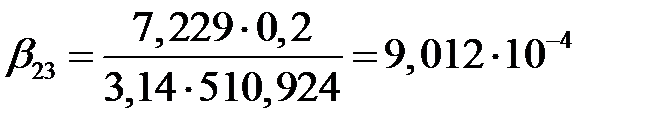
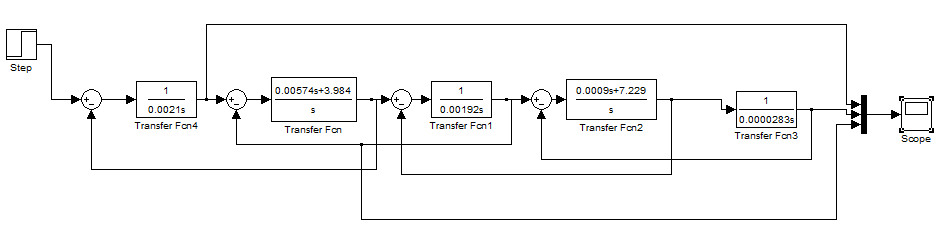
Рис.2.5. Модель трехмассовой последовательности упругой системы.
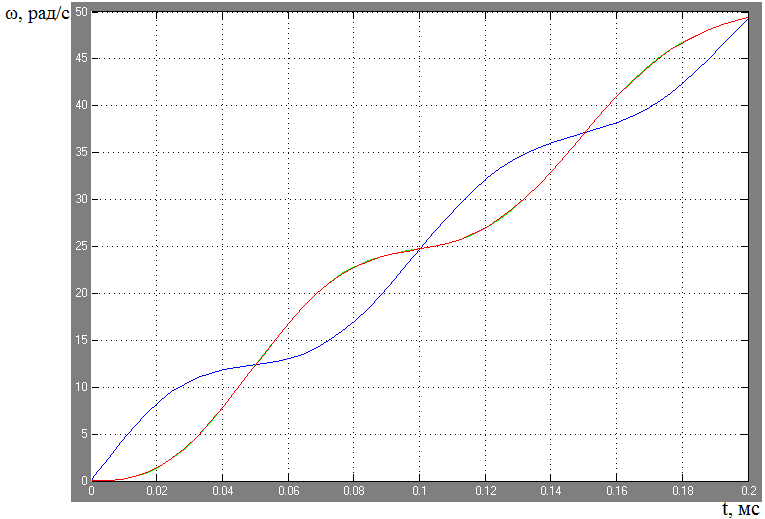
Рис.2.6. Графики пуска электропривода с трехмассовой упругой механической частью с учетом естественного демпфирования.
Из полученных графиков видно, что колебания второй и третьей масс находятся в противофазе с первой массой, следовательно, расчёт проведён правильно.
Приведение к двухмассовой системе
Эквивалентная жесткость двухмассовой упругой системы:
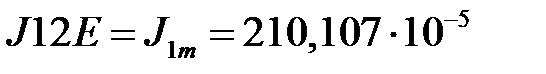 кг∙м2;
кг∙м2;
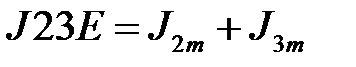 ; (2.19)
; (2.19)
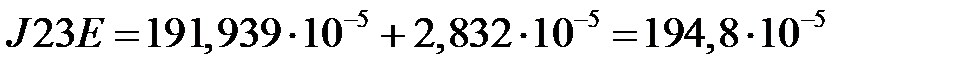 (кг∙м2);
(кг∙м2);
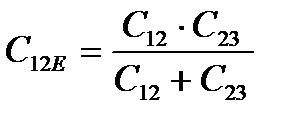 ; (2.20)
; (2.20)
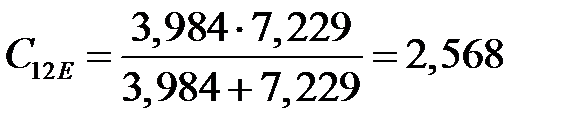 Н∙м2;
Н∙м2;
Соотношение масс:
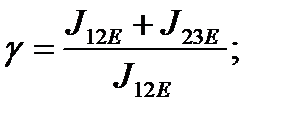 (2.21)
(2.21)
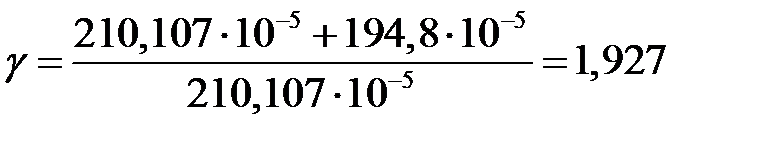 ;
;
Резонансная частота системы:
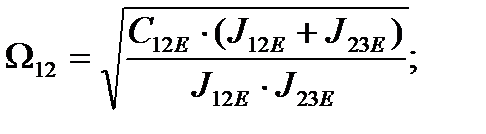 (2.22)
(2.22)
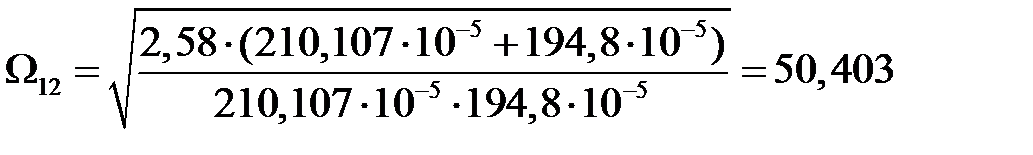 1/с;
1/с;
Резонансная частота второй массы при жесткой заделке первой:
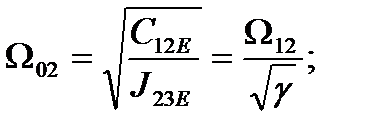 (2.23)
(2.23)
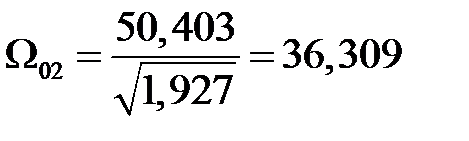 1/с;
1/с;
Коэффициент вязкого трения, приведенный к двигателю:
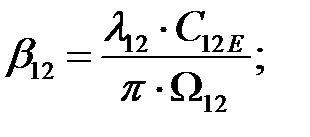 (2.24)
(2.24)
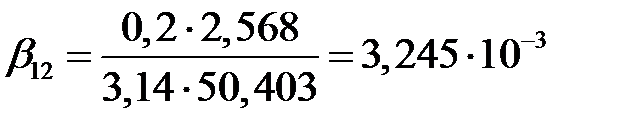 ;
;
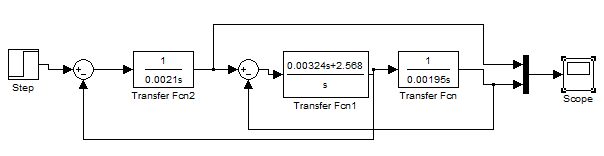
Рис.2.7. Модель двухмассовой последовательности упругой системы.
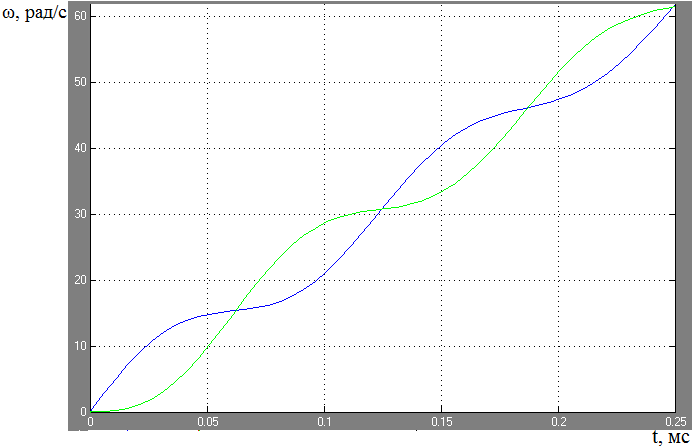
Рис.2.8. Графики пуска электропривода с двухмассовой упругой механической частью с учетом естественного демпфирования.
Характер полученных зависимостей свидетельствует о том, что при М=const из-за влияния диссипативных сил типа внутреннего вязкого трения, колебания скорости постепенно затухают (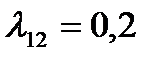 ), однако мгновенные скорости
), однако мгновенные скорости 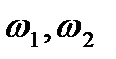 при этом не совпадают, так как содержат колебательные составляющие, причём колебания
при этом не совпадают, так как содержат колебательные составляющие, причём колебания 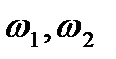 совершаются в противофазе свидетельствуя о том, что система устойчива и расчет произведен правильно.
совершаются в противофазе свидетельствуя о том, что система устойчива и расчет произведен правильно.