В2.1. Принцип умножения
Комбинаторика – раздел математики, в котором изучаются методы подсчета числа комбинаций определенного вида, составленных из элементов определенного множества.
Основным в элементарной комбинаторике является принцип умножения.
Принцип умножения.
Пусть требуется выполнить одно за другим n действий, причем 1-е действие можно выполнить k 1 способами; 2-е – k 2 способами; 3-е – k 3 способами;…; n -е - kn способами. И число способов, которыми можно выполнить каждое действие, не зависит от того, какие способы были выбраны для выполнения предшествующих действий. Тогда число способов, которыми можно выполнить все n действий, равно произведению k 1 × k 2 × k 3 ×... × kn. Это и есть принцип умножения. Проще всего объяснить справедливость принципа умножения можно при помощи диаграммы (рис. 2).
Пример.
У человека имеется 3 рубашки (Р 1, Р 2, Р 3), 2 галстука (Г 1, Г 2) и 2 пары ботинок (Б 1, Б 2). Он признает любое сочетание этих элементов. Сколькими способами он может одеться?
Решение.
Чтобы одеться, человек должен выполнить одно за другим и независимо одно от другого 3 действия:
1. Выбрать рубашку (три способа).
2. Выбрать галстук (два способа).
3. Выбрать ботинки (два способа).
Все способы выбора костюма показаны на диаграмме (рис. 2).
Рис. 2
Всего можно одеться 3 × 2 × 2 = 12 способами.
В2.2. Перестановки, размещения, сочетания
Определение. Перестановкой n данных элементов называется любой упорядоченный набор этих элементов, место элемента в наборе имеет значение.
Пример 1.
Из трех элементов A,B,C можно составить шесть разных перестановок: ABC; ACB; CAB; CBA; BAC; BCA.
Число различных перестановок п элементов обозначается Рп. Выведем формулу подсчета числа Рп, для чего воспользуемся принципом умножения.
Чтобы определить перестановку n данных различных элементов, нужно выполнить одно за другим n действий:
· выбрать первый элемент перестановки (n способов);
· указать второй элемент (n - 1 способ);
…………………………………………;
· назвать последний элемент перестановки (1 способ).
Эти действия выполняются независимо одно от другого. В силу принципа умножения
Pn = n × (n - 1) ×...× 1 = n! (1)
Определение. Размещением, содержащим k различных элементов,выбранных из n имеющихся, называется любой упорядоченный набор k различных элементов, отобранных из n имеющихся различных элементов.
Пример 1.
Из букв A, B, C, D можно составить 12 размещений из двух букв:
AB; BA; AC; CA; AD; DA; BC; CB; BD; DB; CD; DC.
Число различных размещений обозначается символом 
. Выведем формулу его подсчета.
Чтобы составить размещение, нужно выполнить одно за другим и независимо одно от других k действий:
· назвать первый элемент размещения (n способов);
· указать второй элемент (n - 1 способ);
……………………………………………;
· назвать k -й, последний, элемент (n – k + 1 способов).
В соответствии с принципом умножения
= n × (n – 1) ×...× (n – k + 1) =
= 
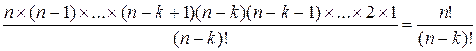(2)
Пример 2. Сколько трех-, четырех-, пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 (0, 1, 2, 3, 4), если
a) повторения цифр запрещены;
b) повторения цифр разрешены.
Решение.
Рассмотрим первый набор чисел.
Если повторения запрещены, то каждое число – размещение из соответствующего количества цифр, следовательно, количество разных трех-, четырех-, пятизначных чисел равно
= 
.
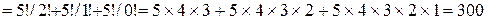Если повторения разрешены, воспользуемся принципом умножения, каждое действие (задание очередной цифры) можно выполнить пятью способами.
Трехзначных чисел всего 5 × 5 × 5 = 125; четырехзначных чисел всего 5 × 5 × 5 ×5 = 625; пятизначных чисел всего 5 × 5 × 5 × 5× 5 = 3125.
Итого 3875 разных чисел.
Рассмотрим второй набор чисел.
Ноль не может стоять первой цифрой в числе, поэтому, если повторения запрещены, то разных трехзначных чисел всего 4 × 4 × 3 = 48;
разных четырехзначных чисел – 4 × 4 × 3 × 2 = 96; разных пятизначных чисел – 4 × 4 × 3 × 2 × 1 = 96. Всего 240 чисел.
Если повторения разрешены, трехзначных чисел всего 4 × 5 × 5 = =100; четырехзначных чисел - 4 × 5 × 5 × 5 = 500; пятизначных чисел - 4 ×
´ 5 × 5 × 5 × 5 = 2500. Всего 3100 чисел.
Определение. Сочетанием, содержащих k различных элементов, выбранных из n имеющихся разных элементов, называется любой неупорядоченный набор, содержащий k различных элементов, отобранных из n данных разных элементов.
В неупорядоченном наборе порядок перечисления элементов не важен.
Пример 1. Из букв A, B, C, D, E можно составить 10 разных сочетаний по три буквы: { A,B,C }; { A,B,D }; { A,B,E }; { A,C,D }; { A,C,E }; { A,D,E }; { B,C,D }; { B,C,E }; { B,D,E }; { C,D,E }.
Подчеркнем, что сочетание { A, B,C } тождественно сочетанию { B, C, А }. Но перестановки АВС и ВСА – различны.
Число разных сочетаний из п элементов по k элементов обозначается символом 
. Выведем формулу подсчета .
Любому неупорядоченному набору (сочетанию), содержащему k разных элементов, можно поставить в соответствие k упорядоченных наборов (перестановок) этих элементов.
Таким образом,
= 
(3)
Числа 
называются биномиальными коэффициентами.