Определение. Перестановка с повторениями, состоящая из n элементов, содержит n 1 одинаковых элементов 1-го вида, n 2 – одинаковых элементов 2-го вида, …, nk одинаковых элементов k -го вида, n = n 1 + n 2+ +…+ nk.
Пример 1. Последовательность 112314123 – это перестановка с повторениями, содержащая n 1 = 4 единицы; n 2 = 2 двойки; n 3 = 3 тройки и n 4 = 1 четверку, n 1 + n 2 + n 3 + n 4 = 10.
Пример другой перестановки этих же цифр – последовательность 231141231. Но если в перестановке с повторениями переставить одинаковые элементы, она не изменится, одинаковые элементы неразличимы между собой.
Число различных перестановок с повторениями обозначим символом 
. Построим расчетную формулу..
Чтобы задать перестановку с повторениями, нужно выполнить одно за другим и независимо одно от других k действий:
· выбрать n 1 мест из n имеющихся для элементов 1-го вида (
способов);
· выбрать n 2 мест из n - 
имеющихся для элементов 2-го вида (
способов);
………………………………………………………………………………..
· выбрать nk мест из n – п 1 - … - 
= nk оставшихся для элементов k -го вида (
= 1 способ).
По принципу умножения
= 
= 
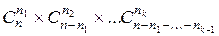. (4)
Пример 2. Сколько чисел, больших 3000000, можно составить изцифр 3, 2, 2, 1, 1, 1, 0.
Решение. На первом месте обязательно должна стоять тройка. Оставшиеся 6 цифр образуют перестановку, в которой повторяются n 1 = 2 двойки; n 2 = 3 единицы и n 3 = 1 ноль. Всего таких перестановок
P 2,3,1 = 
= 60.
Определение. Сочетанием с повторениями из n элементов по k называется неупорядоченный набор, содержащий k элементов, каждый из которых может быть одного из n типов.
Пример 1. Располагая тремя цифрами, 1, 2, 3, составить из них всевозможные сочетания с повторениями, содержащие по 2 элемента.
Решение. Перечислим все такие сочетания: (1, 1); (1, 2); (1, 3); (2, 2); (2, 3); (3, 3). Подчеркнем, что (1, 2) и (2, 1) – это одно и то же сочетание, но 12 и 21 – два разных размещения.
Количество различных сочетаний с повторениями обозначим 
. Выведем формулу для определения .
Чтобы задать сочетание с повторениями, нужно знать, сколько элементов каждого типа оно содержит.
Пусть оно содержит m 1 элементов 1-го типа; m 2 – 2-го типа; … mn – n -го типа, m 1 + m 2 +...+ mn = k.
Закодируем каждое сочетание с повторениями последовательностью из нулей и единиц, устроенной так. Сначала запишем m 1 единиц, потом запишем 0. Затем запишем m 2 единиц и 0, …. Наконец, запишем mn единиц.
Всего последовательность содержит m 1 + m 2 +...+ mn = k единиц и (n - 1) нулей.
В случае примера 1 k = 2, n = 3 и каждая последовательность содержит 2 единицы и 2 нуля.
Запишем последовательности, соответствующие каждому из 6 сочетаний с повторениями: (1, 1) - 1100; (1, 2) - 1010; (1, 3) - 1001; (2, 2) - 0110; (2, 3) - 0101; (3, 3) - 0011.
Таким образом, каждому сочетанию с повторениями соответствует своя последовательность из нулей и единиц, и по каждой такой последовательности однозначно восстанавливается соответствующие ей сочетание с повторениями. Следовательно, число равно числу разных последовательностей из нулей и единиц, содержащих n + k – 1 цифру, причем единиц всего k, а нулей – (n - 1) штук. Всего таких последовательностей 
.
Для примера 1: 
= 
= 6. Итак,
= (5)
Пример 2.
Число неотрицательных решений в целых числах уравнения 
равно 
, ведь всякое решение 
данного уравнения можно трактовать, как сочетание с повторениями, содержащее 
элементов первого типа (
), 
элементов второго типа (
), …, 
элементов n го типа (
), 
.
В2.4. Бином Ньютона
Утверждение. Справедлива формула (формула бинома Ньютона)
.