Скорость и ускорение точки
Пусть в момент времени  положение точки определяется радиусом-вектором
положение точки определяется радиусом-вектором 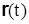 ,а в момент
,а в момент  радиусом-вектором
радиусом-вектором 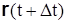 . Вектор
. Вектор
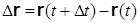
будем называть вектором перемещения точки за время 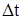 (рис. 3.7).
(рис. 3.7).
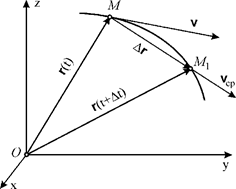 Рис. 3.7.
Рис. 3.7.
| Отношение вектора 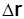 к промежутку времени М называется средней скоростью точки за промежуток времени к промежутку времени М называется средней скоростью точки за промежуток времени 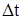
 .
Скоростью в данный момент времени называется предел отношения вектора .
Скоростью в данный момент времени называется предел отношения вектора
|
перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, т.е.
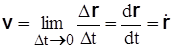 . (3.9)
. (3.9)
Из этого определения видно, что скорость точки равна производной радиуса-вектора точки по времени. На рис. 3.7 показаны средняя скорость 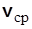 и скорость
и скорость 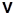 точки М. Как следует из общей теории, скорость точки
точки М. Как следует из общей теории, скорость точки 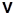 – этор вектор, направленный по касательной к траектории в сторону движения точки.
– этор вектор, направленный по касательной к траектории в сторону движения точки.
3.2.1. Скорость точки при координатном способе задания движения
Декартова система координат
Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т.е. пусть заданы координаты точки как функции времени
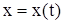 ,
,  ,
, 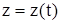 .
.
Согласно выражению (3.6) имеем 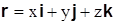 .
.
Так как единичные векторы  выбранной системы координат постоянны, то на основании формулы (3.9) получаем
выбранной системы координат постоянны, то на основании формулы (3.9) получаем
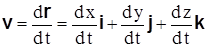 .
.
 Рис. 3.8.
Рис. 3.8.
| На рис. 3.8 показано разложение скорости на составляющие по осям координатной системы Oxyz.
Таким образом, проекции скорости 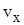 , , 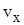 , , 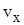 на координатные оси будут на координатные оси будут
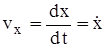 , , 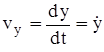 , ,  . .
|
т.е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.
Модуль скорости определяется формулой
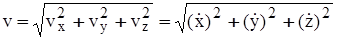 , (3.10)
, (3.10)
а направление скорости – направляющими косинусами
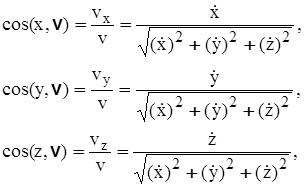 (3.11)
(3.11)
Если модуль скорости не изменяется с течением времени, то движение называется равномерным.
Полярные координаты
Введем в рассмотрение единичные векторы: 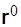 , направленный по радиусу-вектору в сторону возрастания
, направленный по радиусу-вектору в сторону возрастания 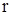 , и
, и  , повернутый относительно
, повернутый относительно 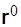 на угол
на угол 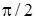 в сторону возрастания угла
в сторону возрастания угла  (рис. 3.9). Единичные векторы
(рис. 3.9). Единичные векторы 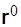 и
и  могут быть представлены через единичные векторы
могут быть представлены через единичные векторы 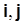 координатных осей:
координатных осей:
 ,
,
 .
.
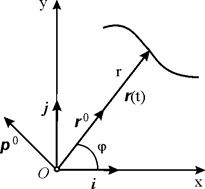 Рис.3.9.
Рис.3.9.
| 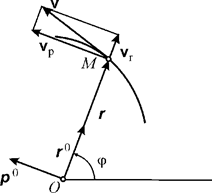 Рис. 3.10.
Рис. 3.10.
|
Производные по времени от единичных векторов 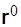 ,
,  определяются соотношениями
определяются соотношениями
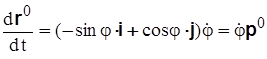 , (3.12)
, (3.12)
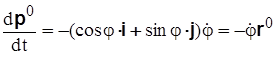 . (3.13)
. (3.13)
Радиус-вектор 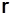 , определяющий положение точки, может быть представлен в виде
, определяющий положение точки, может быть представлен в виде 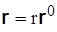 (рис. 3.9). При движении точки меняются как модуль, так и направление радиуса-вектора
(рис. 3.9). При движении точки меняются как модуль, так и направление радиуса-вектора 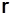 , следовательно, и
, следовательно, и  , и
, и 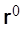 являются функциями времени. На основании равенства (3.9) имеем
являются функциями времени. На основании равенства (3.9) имеем
 .
.
Используя соотношение (3.12), будем иметь
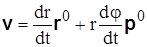 .
.
Полученная формула дает разложение вектора скорости на две взаимно перпендикулярные составляющие: радиальную 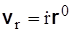 и поперечную
и поперечную 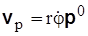 (рис. 3.10).
(рис. 3.10).
Проекции скорости на радиальное и поперечное направления
 и
и  (3.14)
(3.14)
называются соответственно радиальной и поперечной скоростями. Модуль скорости находится по формуле
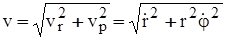 . (3.15)
. (3.15)
3.2.2. Скорость точки при естественном способе задания движения. Пусть точка М движется по какой-либо кривой (рис. 3.11). За промежуток времени 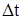 точка переместится по кривой из положения М в положение М 1. Дуга
точка переместится по кривой из положения М в положение М 1. Дуга  , если движение точки происходит в сторону положительного отсчета дуги (рис. 3.11 а), и
, если движение точки происходит в сторону положительного отсчета дуги (рис. 3.11 а), и  , если движение происходит в противоположную сторону (рис. 3.11 б). На основании (3.9)
, если движение происходит в противоположную сторону (рис. 3.11 б). На основании (3.9)
имеем 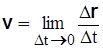 .
.
Перепишем это равенство в виде
 .
.
Так как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей ММ 1совпадает с направлением касательной к кривой в точке М, то
 ,
,
где 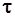 – единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.
– единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.
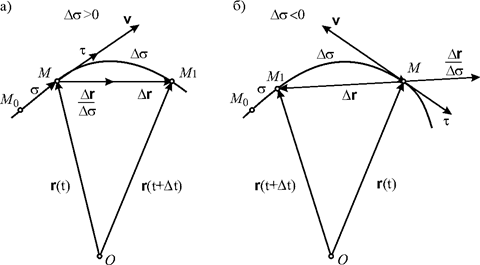 Рис. 3.11.
Рис. 3.11.
|
Действительно, если  , то вектор
, то вектор  направлен в сторону
направлен в сторону  (см. рис. 3.11 а), а при
(см. рис. 3.11 а), а при  вектор
вектор  направлен в сторону, противоположную
направлен в сторону, противоположную  (см. рис. 3.11 б). В обоих случаях этот вектор, а следовательно, и его предел
(см. рис. 3.11 б). В обоих случаях этот вектор, а следовательно, и его предел  , направлены в сторону возрастания дуги
, направлены в сторону возрастания дуги  (на рис. 3.11 положительное направление отсчета дуги
(на рис. 3.11 положительное направление отсчета дуги  выбрано вправо от начала отсчета М 0).
выбрано вправо от начала отсчета М 0).
Учитывая, что 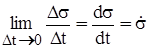 ,
,
имеем 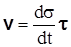 . (3.16)
. (3.16)
Обозначая 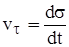 , получим
, получим
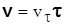 . (3.17)
. (3.17)
Из формулы (3.17) следует, что  . Очевидно, что
. Очевидно, что 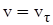 , если движение происходит в сторону положительного отсчета дуги, и
, если движение происходит в сторону положительного отсчета дуги, и  , если движение происходит в противоположную сторону.
, если движение происходит в противоположную сторону.
Так как проходимый точкой путь всегда положителен, то элемент пути
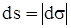
и, следовательно, модуль скорости можно определить по формуле
 .
.
Ускорение точки
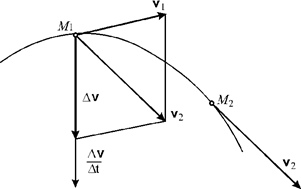 Рис. 3.12.
Рис. 3.12.
| Предположим, что в момент времени  скорость точки равна скорость точки равна  , а в момент времени , а в момент времени  будет будет 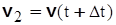 (рис. 3.12). Приращение вектора скорости (рис. 3.12). Приращение вектора скорости 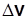 за промежуток времени за промежуток времени 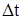 найдем как разность векторов найдем как разность векторов  и и  , ,
|
параллельно перенося вектор  в точку М 1
в точку М 1
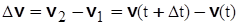 .
.
Отношение

называется средним ускорением точки за промежуток времени 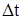 .
.
Ускорением  точки в данный момент времени называется предел отношения приращения скорости
точки в данный момент времени называется предел отношения приращения скорости 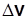 к приращению времени
к приращению времени 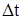 при условии, что последнее стремится к нулю, т.е.
при условии, что последнее стремится к нулю, т.е.
 , (3.18)
, (3.18)
или 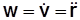 .
.
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса-вектора точки.
3.3.1. Ускорение при координатном способе задания движения
Декартова система координат
Пусть движение точки задано в прямоугольной системе координат:
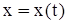 ,
, 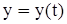 ,
, 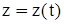 .
.
Представляя вектор скорости точки в виде
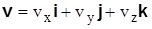 ,
,
на основании (3.18) будем иметь
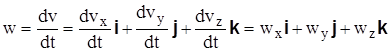 ,
,
где
 , (3.19)
, (3.19)
т.е. проекция ускорения точки на какую-либо координатную ось равна первой производной по времени от соответствующей проекции скорости точкии второй производной по времени от соответствующей координаты точки.
Модуль ускорения определяется по формуле
 , (3.20)
, (3.20)
а направление вектора ускорения – направляющими косинусами:
 (3.21)
(3.21)
Полярные координаты
Пусть координаты точки заданы как функции времени 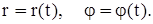
Согласно (3.14) имеем 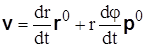 .
.
На основании (3.18) получим
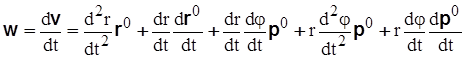 ,
,
но так как 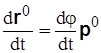 ,
, 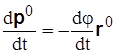 ,
,
то  .
.
Отсюда находим проекции ускорения на радиальное и поперечное направления
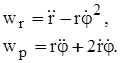 (9.22)
(9.22)
Модуль и направление вектора ускорения определяются по формулам
 ,
,

3.3.2. Ускорение при естественном способе задания движения
Предварительно познакомимся с необходимыми сведениями из дифференциальной геометрии. Рассмотрим пространственную кривую. Пусть  – единичный вектор касательной, проведенной в какой-либо – единичный вектор касательной, проведенной в какой-либо
|  Рис. 3.13.
Рис. 3.13.
|
точке М этой кривой (рис. 3.13). Возьмем теперь на кривой точку М 1, близкую к точке М, и обозначим единичный вектор касательной в этой точке через 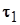 . Параллельно перенеся вектор
. Параллельно перенеся вектор 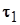 в точку М, проведем плоскость через векторы
в точку М, проведем плоскость через векторы  и
и 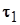 приложенные в точке М.
приложенные в точке М.
При стремлении точки М 1к точке М эта плоскость в пределе займет определенное положение. Полученную таким образом плоскость называют соприкасающейся плоскостью в точке М. Отметим, что если рассматриваемая кривая плоская, то она целиком будет расположена в соприкасающейся плоскости.
Плоскость, проведенную через точку М перпендикулярно касательной, называют нормальной плоскостью. Линия пересечения соприкасающейся и
| нормальной плоскостей определяет главную нормаль к кривой в точке М. Плоскость, проведенную через точку М перпендикулярно главной нормали, называют спрямляющей плоскостью. На рис. 3.14 соприкасающаяся, |  Рис. 3.14.
Рис. 3.14.
|
нормальная и спрямляющая плоскости обозначены соответственно цифрами I, II и III.
Линия пересечения спрямляющей и нормальной плоскостей определяет бинормаль ккривой.
Таким образом, в каждой точке кривой можно указать три взаимно перпендикулярных направления: касательной, главной нормали и бинормали. Принимая эти направления за координатные оси, введем единичные векторы этих осей.
Единичный вектор касательной  нами уже был введен. Единичный вектор
нами уже был введен. Единичный вектор 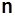 , направленный в сторону вогнутости кривой, будет единичным вектором главной нормали. Направление единичного вектора бинормали
, направленный в сторону вогнутости кривой, будет единичным вектором главной нормали. Направление единичного вектора бинормали 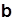 определим из требования, чтобы касательная, главная нормаль и бинормаль, направления которых определяются векторами
определим из требования, чтобы касательная, главная нормаль и бинормаль, направления которых определяются векторами 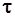 ,
, 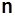 ,
, 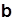 , образовывали правую систему осей, т.е.
, образовывали правую систему осей, т.е. 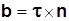 Полученный трехгранник, составленный из соприкасающейся, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Векторы
Полученный трехгранник, составленный из соприкасающейся, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Векторы 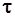 ,
, 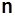 ,
, 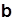 являются единичными векторами осей естественного трехгранника (рис. 3.14).
являются единичными векторами осей естественного трехгранника (рис. 3.14).
Обозначим через 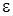 величину угла между вектором
величину угла между вектором 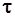 , проведенным в точке М, и вектором
, проведенным в точке М, и вектором  , проведенным в точке М 1, близкой к точке М. Этот угол называется углом смежности (рис. 3.15 а).
, проведенным в точке М 1, близкой к точке М. Этот угол называется углом смежности (рис. 3.15 а).
 Рис. 3.15.
Рис. 3.15.
|
Кривизной кривой в точке М называют предел отношения угла смежности 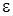 к абсолютному значению длины дуги
к абсолютному значению длины дуги  , т.е.
, т.е.
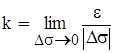 . (3.23)
. (3.23)
Радиусом кривизны кривой в точке М называется величина, обратная кривизне
 . (3.24)
. (3.24)
Вектор скорости согласно выражению (3.17) можно представить в виде
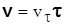 .
.
На основании формулы (3.18) имеем
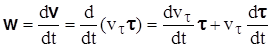 . (9.25)
. (9.25)
Определим величину и направление вектора  .
.
Пусть в момент времени  точка находится в положении М на траектории, а в момент времени
точка находится в положении М на траектории, а в момент времени  – в положении М 1. Перенося вектор их в точку М, найдем приращение вектора
– в положении М 1. Перенося вектор их в точку М, найдем приращение вектора  за промежуток времени
за промежуток времени 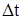 (рис. 3.15 а)
(рис. 3.15 а)
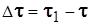 .
.
Вектор  при движении точки в сторону положительного отсчета дуги направлен в сторону вогнутости траектории (рис. 3.15 а), а при движении точки в сторону отрицательного отсчета дуги направлен в сторону выпуклости траектории (рис. 3.15 б). Найдем производную вектора
при движении точки в сторону положительного отсчета дуги направлен в сторону вогнутости траектории (рис. 3.15 а), а при движении точки в сторону отрицательного отсчета дуги направлен в сторону выпуклости траектории (рис. 3.15 б). Найдем производную вектора 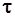 :
:
 .
.
Вектор 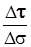 всегда направлен в сторону вогнутости траектории (см. рис. 3.15 а и б) и лежит в плоскости, проходящей через точку М и векторы
всегда направлен в сторону вогнутости траектории (см. рис. 3.15 а и б) и лежит в плоскости, проходящей через точку М и векторы 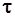 и
и  (плоскость МАВ). Следовательно, вектор
(плоскость МАВ). Следовательно, вектор  лежит в соприкасающейся плоскости, т.к. при
лежит в соприкасающейся плоскости, т.к. при  плоскость МАВ совпадает с соприкасающейся плоскостью к траектории в точке М.
плоскость МАВ совпадает с соприкасающейся плоскостью к траектории в точке М.
Дифференцируя тождество  по
по  , получим
, получим
 ,
,
т.е. скалярное произведение 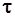 на
на  равно нулю, а это значит, что вектор
равно нулю, а это значит, что вектор  перпендикулярен
перпендикулярен 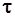 . Таким образом, вектор
. Таким образом, вектор  лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен
лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен 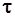 ; следовательно, он направлен по главной нормали к центру кривизны.
; следовательно, он направлен по главной нормали к центру кривизны.
Определим теперь модуль вектора  . Из равнобедренного треугольника АМВ (см. рис. 3.15 а)найдем
. Из равнобедренного треугольника АМВ (см. рис. 3.15 а)найдем 
или, используя равенства (3.23) и (3.24), получим
 .
.
Учитывая, что 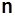 есть единичный вектор главной нормали, будем иметь
есть единичный вектор главной нормали, будем иметь
 .
.
Значит,  ,
,
и, следовательно,
 , (3.26)
, (3.26)
т.к. 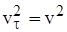 .
.
Из этой формулы следует, что вектор ускорения лежит в соприкасающейся плоскости.
Составляющие ускорения по направлениям 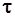 и
и 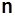 соответственно равны
соответственно равны
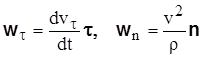 .
.
Проекция ускорения на направление 
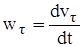 (3.27)
(3.27)
называется касательным (тангенциальным) ускорением. Проекция ускорения на главную нормаль
 (3.28)
(3.28)
называется нормальным ускорением. Касательное ускорение характеризует изменение модуля скорости, а нормальное ускорение характеризует изменение скорости по направлению. Модуль вектора ускорения равен
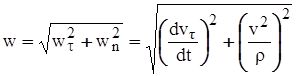 . (3.29)
. (3.29)
Касательное ускорение 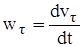 равно нулю при движении точки с постоянной по модулю скоростью и в моменты времени, в которые скорость
равно нулю при движении точки с постоянной по модулю скоростью и в моменты времени, в которые скорость 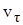 достигает экстремальных значений.
достигает экстремальных значений.
Если 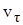 и
и 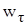 одного знака, то модуль скорости
одного знака, то модуль скорости  точки возрастает и движение в этом случае называется ускоренным.Если же
точки возрастает и движение в этом случае называется ускоренным.Если же 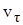 и
и 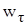 разных знаков, то модуль скорости
разных знаков, то модуль скорости  точки убывает и движение будет замедленным. При
точки убывает и движение будет замедленным. При 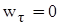 модуль скорости остается постоянным – движение равномерное.
модуль скорости остается постоянным – движение равномерное.