1. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25. Ответ :16
2. Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°. Ответ: 82°, 42°, 56°
3. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус равно 8. Ответ: 4
4. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC. Ответ:15
5. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB =16, DC = 24 , AC = 25. Ответ:15
6. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD. Ответ: 10
7. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 . Ответ: 40
8. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34. Ответ: 68
9. Прямая, параллельная основаниям 
и 
трапеции 
, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны 
и 
в точках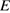 
и 
соответственно. Найдите длину отрезка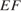 
, если 
, 
. Ответ: 12
10. В прямоугольном треугольнике АВС с прямым угломС известны катеты: АС=6, ВС=8. Найдите медиану СК этого треугольника. Ответ:5
11. Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если∠АВС = 20°. Ответ:35
12. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD. Ответ: 20
13. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4. Ответ: 8
14. Катет и гипотенуза прямоугольного треугольника равны 18 и 30. Найдите высоту, проведённую к гипотенузе. Ответ: 14,4
15. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16. Ответ: 16
16. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 18, а сторона BC в 1,2 раза меньше стороны AB. Ответ:15
17. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28. Ответ: 7
18. Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30° и 90°. Ответ: 1:2
19. Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.
Ответ: 12
20. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСД пересекаются в точке F. Найдите AB, если AF=24. BF=10 . Ответ: 26
21. Диагонали АС и ВД трапеции АВСД пересекаются в точке О . Площади треугольников АОД и ВОС равны соответственно 16 и 9 . Найдите площадь трапеции. Ответ: 49
22. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции. Ответ: 
23. Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции. Ответ: 9
24. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34. Ответ: 17
25. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 19, а расстояние от точки K до стороны AB равно 7. Ответ: 266
26. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD = 25. Ответ: 
