МАТРИЦЫ, ИХ ВИДЫ. ОПЕРАЦИИ НАД МАТРИЦАМИ
Справочный материал
Определение матрицы
Матрицей размерностью m x n (m - строк, n - столбцов) называют прямоугольную таблицу чисел
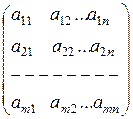 .
.
Обозначение матрицы
Матрицу обозначают большими буквами латинского алфавита A, B, C, D, E,… X, Y, Z,… и кратко записывают так:
A = 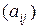

 1≤ i≤ m, 1≤ j ≤ n.
1≤ i≤ m, 1≤ j ≤ n.
Нуль матрица
Нуль-матрица (нулевая матрица) O состоит из нулей.
Матрица-строка
Матрица-строка ( 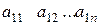 ) имеет размерность 1 x n, а матрице-столбцу соответствует размерность m x 1.
) имеет размерность 1 x n, а матрице-столбцу соответствует размерность m x 1.
Квадратная матрица
При m = n матрицу называют квадратной порядка n:
A = 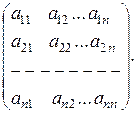

Диагональная матрица
Диагональной D называют квадратную матрицу вида
D = 
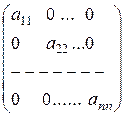 .
.
Единичная матрица
Единичной E называют такую диагональную матрицу, для которой 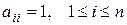 .
.
Умножение матрицы на число
При умножении матрицы 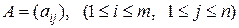 , на число
, на число 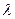 все элементы умножаются на это число:
все элементы умножаются на это число: 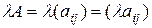 .
.
Сложение двух матриц
При сложении двух матриц одной размерности складываются соответствующие элементы этих матриц:
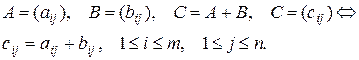
Свойства матриц
На основании определения указанных операций нетрудно установить их свойства:
1) A+B=B+A (переместительный закон сложения),
2) (A+B)+C=A+(B+C) (сочетательный закон),
3) A+0=A,
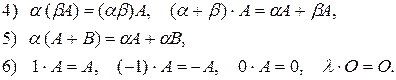
Умножение двух матриц
Рассмотрим две матрицы:
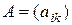 размерностью m
размерностью m 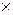 p и
p и 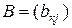 размерностью p
размерностью p 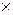 n такие, что число столбцов матрицы A равно числу строк матрицы B.
n такие, что число столбцов матрицы A равно числу строк матрицы B.
Для таких матриц определим их произведение:
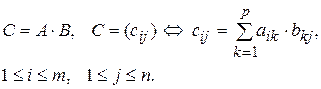
Таким образом, элемент 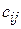 матрицы
матрицы 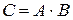 равен сумме парных произведений элементов i - й строки матрицы A и j- го столбца матрицы B.
равен сумме парных произведений элементов i - й строки матрицы A и j- го столбца матрицы B.
· В тех случаях, когда произведение матриц определено, оно обладает следующими свойствами:
1) AB≠BA (переместительный закон, вообще говоря, не справедлив);
2) (A+B)C=AC+BC, C(A+B)=CA+CB (распределительные законы);
3) (AB)C=A(BC) (сочетательный закон).
· Для квадратной матрицы A и матрицы Е той же размерности справедливы равенства АЕ=ЕА=А.
Примеры решения задач
1. Даны две матрицы 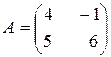 и B =
и B = 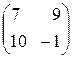 .
.
Найти матрицу C = 3A-2В.
Решение. С=3А+(-2)В. Найдем матрицы
3А= 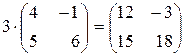 и (-2)В=(-2)
и (-2)В=(-2) 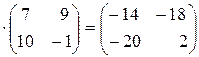 .
.
Складывая эти матрицы, получим
С= 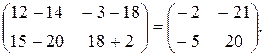
Ответ: 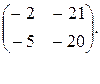
3. Найти матрицу АВ, если А = 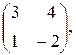 В=
В= 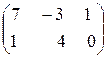 .
.
Решение. Применяя правило умножения матриц, получаем
АВ = 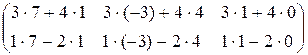 =
= 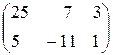 .
.
Если будет необходимо найти произведение ВА для заданного условия, то произведение ВА не определено, поскольку матрица В имеет три столбца, а матрица А - две строки.
Ответ: 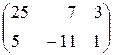 .
.
4. Даны матрицы А и В.
А= 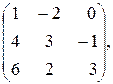 В=
В= 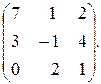
Найти матрицу С=3А-2АВ+5Е.
Решение. При умножении матрицы на число все её элементы умножаются на это число, поэтому
ЗА= 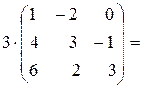
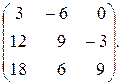
Перемножим матрицы А и В, применив правило умножения матриц:
АВ= 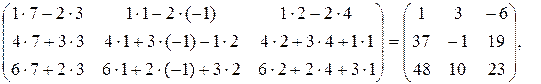
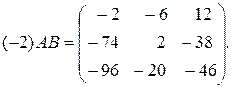
Используя определение единичной матрицы Е, найдем матрицу 5Е:
5Е=5× 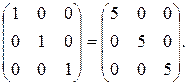
Применив правило сложения матриц, найдем матрицу С=3 А +(-2)× АВ +5 Е:
С= 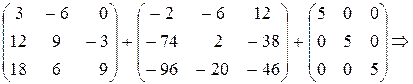
С= 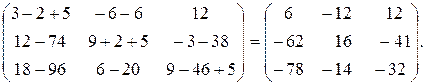
Ответ: 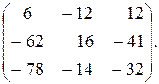
5. В условиях задачи 4 найти матрицы АВ и ВА.
Решение. Матрица АВ найдена при решении задачи 4.
АВ = 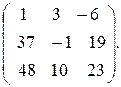
Найдем матрицу ВА:
ВА= 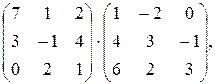
ВА= 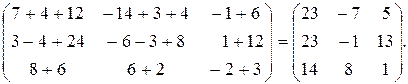
При решении получилось: АВ 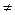 ВА. Это не случайно, так как умножение матриц свойством коммутативности не обладает.
ВА. Это не случайно, так как умножение матриц свойством коммутативности не обладает.
Ответ: АВ= 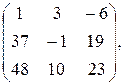 ВА=
ВА= 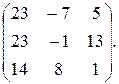

Упражнения для самостоятельного решения
9. Вычислить матрицу А2, если
А= 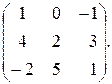
10. Найти матрицу АВС+2А-5Е, если
А= 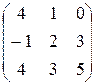 , В=
, В= 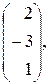 С=
С= 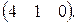
11. Найти матрицы АВ и ВА, если А= 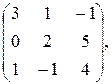 В=
В= 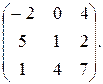
2. ОПРЕДЕЛИТЕЛИ КВАДРАТНЫХ МАТРИЦ
Справочный материал
Каждой квадратной матрице A ставится в соответствие число | А |, называемое определителем. Понятие определителя связано с решением систем линейных уравнений.
Определитель матрицы второго порядка 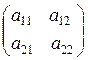 обозначается и вычисляется так:
обозначается и вычисляется так:
Δ 2= 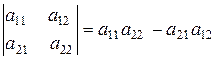 .
.
Определитель второго порядка равен разности произведений элементов главной 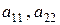 и побочной
и побочной 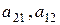 диагоналей
диагоналей
.
1.Вычислить определитель 3-го порядка 1) по правилу Саррюса (правило треугольников). Это правило заключается в равенстве

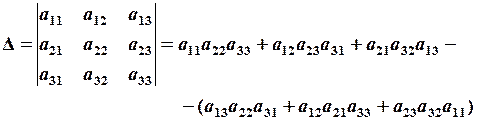 .
.
Таким образом,
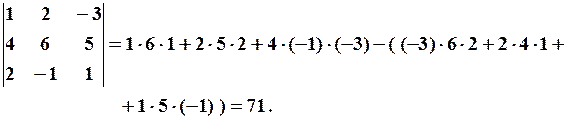
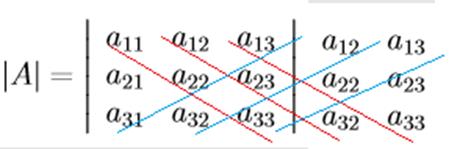
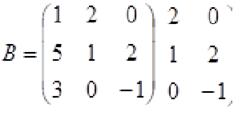
2) Второе правило вычисления 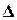 Для квадратной матрицы
Для квадратной матрицы
A= 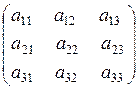
определитель третьего порядка определим так:
Δ 3=|А|= 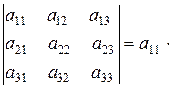
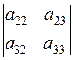 -
- 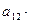
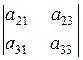 +
+ 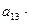
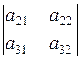 . (1)
. (1)

Равенство (1) называют разложением определителя третьего порядка по элементам первой строки. Для более компактной записи такого разложения вводят понятие алгебраического дополнения элемента определителя.
Минор 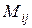 элемента
элемента 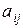 - это определитель, получаемый вычеркиванием
- это определитель, получаемый вычеркиванием
i -й строки и j -го столбца определителя Δ.
Например, M11 = 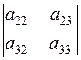 , M23=
, M23= 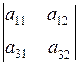 .
.
Алгебраическое дополнение Aij элемента 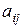 определяется равенством
определяется равенством
Aij= 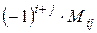 .
.
Например, A11= 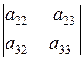 , A23 = -
, A23 = - 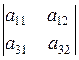 .
.
Знаки алгебраических дополнений символически изобразим так: 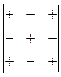 .
.
На основании понятия алгебраического дополнения выражение (1) запишем в следующем виде:
Δ = 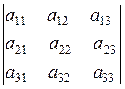 =
= 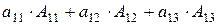 .
.
Нетрудно убедиться, что таким же образом определитель можно разложить по элементам любой строки или любого столбца.
Например, Δ = 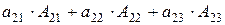 или
или
Δ = 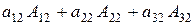 .
.
Определитель
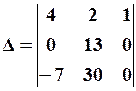
разложим по элементам третьего столбца, т.е.
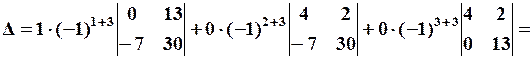
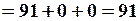 .
.
Как видно из приведенных примеров, вычисление определителей значительно упрощается, если какой-нибудь ряд определителя имеет только один элемент, отличный от нуля. Это можно всегда достигнуть, используя свойства определителей. В определителе
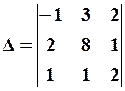
умножим первую строку на 2 и прибавим ко второй, прибавим первую строку к третьей, получим
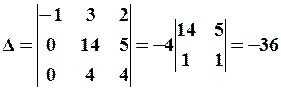 .
.
Примеры решения задач
15. Вычислить определители:
а) 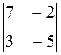 , б)
, б) 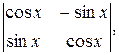 в)
в) 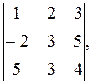 г)
г) 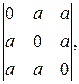
Решение:
а) 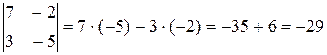 .
.
б) 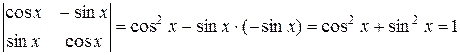 .
.
в) Разложим определитель по элементам первой строки:
 Δ =
Δ = 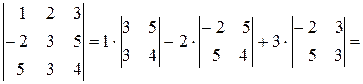
=12-15-2×(-8-25)+3×(-6-15) = -3+66-63=0.
Используя свойство 10, вычисление определителя можно упростить. Для этого в какой-либо строке (столбце) сделаем два нуля: первый столбец последовательно умножим сначала на (-2), затем на (-3) и прибавим ко второму и третьему столбцам соответственно:
D= 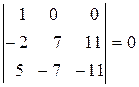 в силу свойства 3, так как элементы второго и третьего столбцов пропорциональны.
в силу свойства 3, так как элементы второго и третьего столбцов пропорциональны.
г) Разложим определитель по элементам первого столбца:
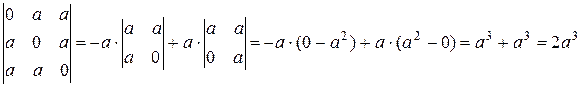 .
.
17.  Решить уравнения:
Решить уравнения:
а) 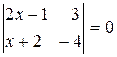 , б)
, б) 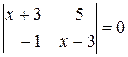 ,
,
в) 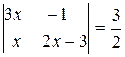 , г)
, г) 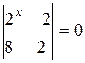 , д)
, д) 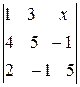 =0.
=0.
Решение:
а) Раскроем определитель второго порядка в левой части уравнения:
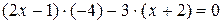 ,
, 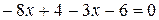 ;
;
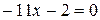 , -11x=2,
, -11x=2, 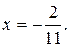

б) 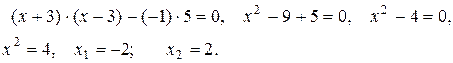
в) 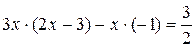 ,
, 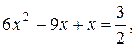
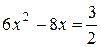 ,
, 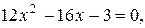
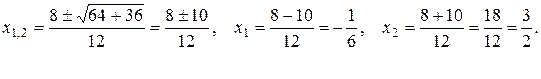
г) 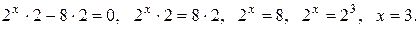
д) Умножив элементы первого столбца на (-3), прибавим их к соответствующим элементам второго столбца и получим
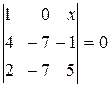 .
.
Вынесем из второго столбца (-7) и затем сократим на (-7) обе части уравнения:
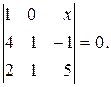
Разложим определитель по элементам первой строки:
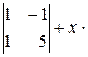
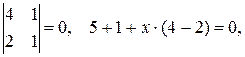
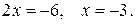
Ответ: а) 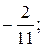 б)±2; в) x1= -
б)±2; в) x1= - 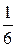 , x2=
, x2= 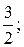 г)3; д)-3.
г)3; д)-3.
2.3. Упражнения для самостоятельного решения
19. Вычислить определители:
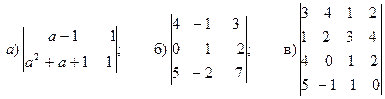
20. Вычислить определитель матрицы А:
А= 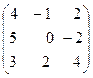 .
.
21. Решить уравнения:
а) 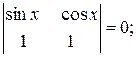 б)
б) 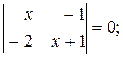 в)
в) 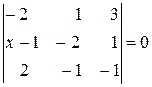 .
.
22. Решить неравенства:
а) 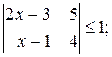 б)
б) 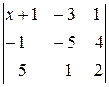 > 0.
> 0.
3. СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ. ФОРМУЛЫКРАМЕРА
Справочный материал
Не ограничивая общности рассуждений, рассмотрим систему трех линейных уравнений с тремя неизвестными:
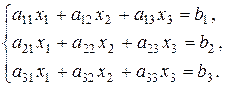 (2)
(2)
Введем главный определитель системы, составленный из коэффициентов при неизвестных
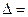
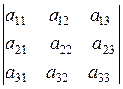 . (3)
. (3)
Если D¹0, то система (2) имеет единственное решение, которое можно найти по формулам Крамера:
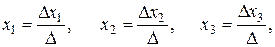 (4)
(4)
где определитель 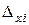 получен из D (3) заменой в нем столбца коэффициентов при
получен из D (3) заменой в нем столбца коэффициентов при 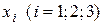 столбцом свободных членов.
столбцом свободных членов.
Примеры решения задач
23. Решить системы, применив формулы Крамера:
а) 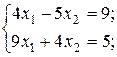 б)
б) 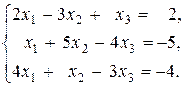
Решение:
а) Определитель системы
D= 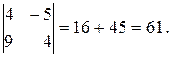
Вычислим определители: заменяем в D первый столбец
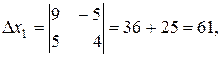
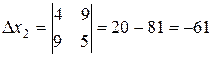 .
.
Тогда 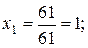
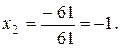
б) Вычислим определитель системы, составленный из коэффициентов при неизвестных:
D = 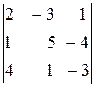 .
.
Умножим элементы третьего столбца на (-2) и прибавим к элементам первого, а затем умножим на 3 и прибавим к элементам второго столбца.
D= 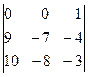 .
.
Разложим этот определитель по элементам первой строки и получим
D = 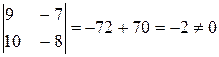 .
.
Вычислим определитель 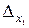 , заменив в определителе D первый столбец (коэффициентов при
, заменив в определителе D первый столбец (коэффициентов при 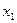 ) столбцом свободных членов.
) столбцом свободных членов.
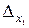
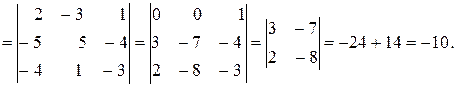
Аналогично находим:
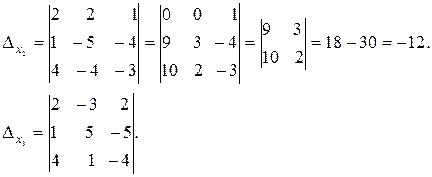

Для вычисления 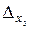 к первой строке прибавим вторую, умноженную на
к первой строке прибавим вторую, умноженную на
(-2), и к третьей строке прибавим вторую, умноженную на (-4).
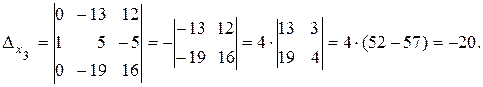
На основании формул Крамера (4) находим решение системы:
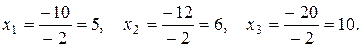
Ответ: а) x1 =1, x2 = -1; б) x1 = 5, x2 = 6, x3 = 10.
24. Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства указаны в табл. 3. Определить объем выпуска продукции каждого вида при заданных запасах сырья.
Таблица 3
| Вид сырья | Расход сырья по видам продукции, вес. ед. изд. | Запас сырья, вес. ед. | ||
Решение. Пусть xi - объем выпуска продукции i -го вида, i =1, 2, 3. При условии полного расхода запасов каждого вида сырья составим балансовые соотношения:
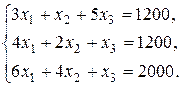
Вычислим определитель этой системы:
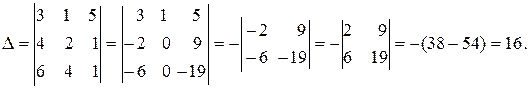
D ¹0, поэтому систему можно решить, применив формулы Крамера.
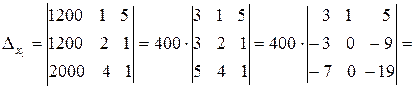
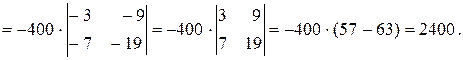
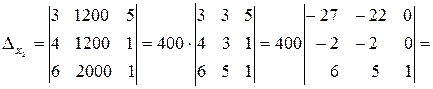
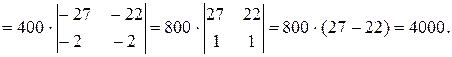
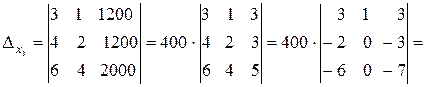

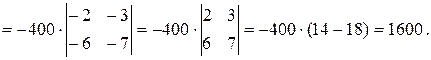
Тогда 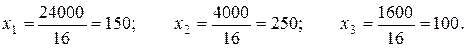
Ответ: При заданных запасах сырья объемы выпуска продукции по каждому виду составят соответственно 150, 250 и 100 условных единиц.
3.3. Упражнения для самостоятельного решения
Решить системы линейных уравнений:
25. 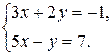 26.
26. 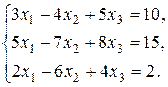 27.
27. 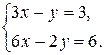
28. 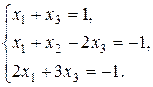

30. Фабрика специализируется на выпуске изделий трех видов, используя при этом сырье трех видов S1, S2 , S3. Нормы расхода каждого из них на одно изделие и объем расхода сырья на 1 день задаются табл. 4.
Таблица 4
| Вид сырья | Нормы расхода сырья на... изделие, усл. ед. | Расход сырья на один день, усл. ед. | ||
| I изделие | II изделие | III изделие | ||
| S1 | ||||
| S2 | ||||
| S3 |
Найти ежедневный объем выпуска каждого вида изделия.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Контрольная работа № 1
Задание 1. Операции над матрицами
91 – 100. Даны матрицы А и В. В №№ 91 - 95 найти матрицу С;
в №№ 96 - 100 найти матрицы АВ и ВА.
91. А = 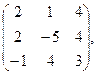
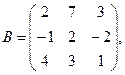
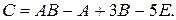
92. А = 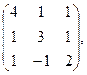
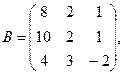
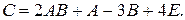
93. А = 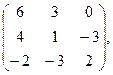
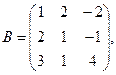
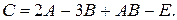
94. А = 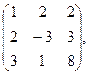
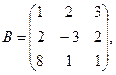
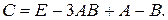
95. А = 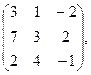
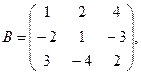
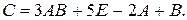
96. А = 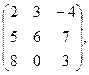
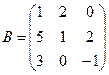 .
.
97. А = 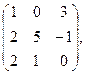
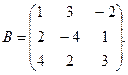
98. А = 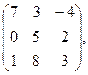
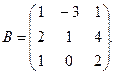
99. А = 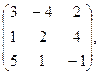
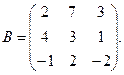
100. А = 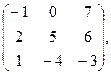
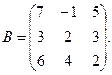
Задание 3. Решение систем линейных уравнений методами Крамера и матричным
111 - 120. Решить систему линейных уравнений, применив формулы Крамера
111. 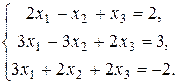 112.
112. 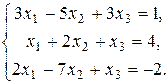
113. 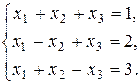 114.
114. 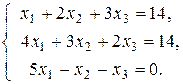
115. 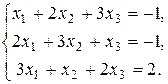 116.
116. 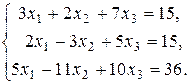
117. 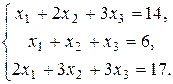 118.
118. 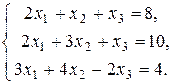
119. 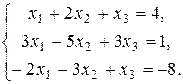 120.
120. 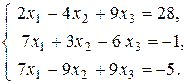
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Вариант 1
1. Решить уравнение 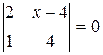 .
. 
2. Решить систему 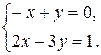
3. Вычислить 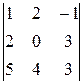 .
.
4. Решить систему по формулам Крамера: 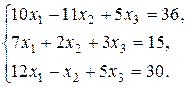
5. Найти матрицу С=АВ-2А+Е, если даны матрицы А и В:
А = 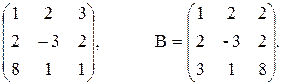
7. Решить систему матричным методом: 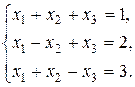
8. Решить систему методом Гаусса и Жордана - Гаусса:
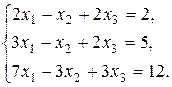
Вариант 2
1. Решить уравнение 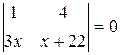 .
.
2. Решить систему 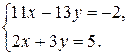

3. Вычислить 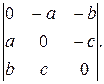
4. Решить систему 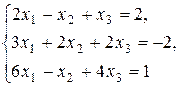 по формулам Крамера.
по формулам Крамера.
5. Найти матрицу С=2А-АВ+4Е, если
А = 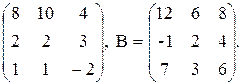
6. А = 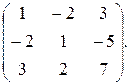 Найти матрицу А
Найти матрицу А 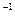 . Показать, что АА
. Показать, что АА 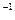 =Е.
=Е.
7. Решить систему матричным методом: 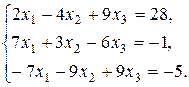
8. Решить систему методом Гаусса и Жордана - Гаусса:
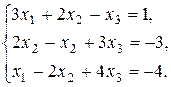
Вариант 3
1. Решить уравнение 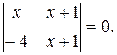
2. Решить систему 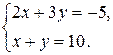
3. Вычислить 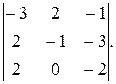
4. Решить систему по формулам Крамера: 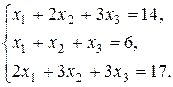
5. А = 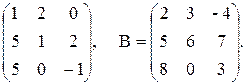 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 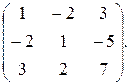 Найти матрицу А
Найти матрицу А 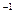 . Показать, что АА
. Показать, что АА 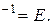
7. Решить систему матричным методом: 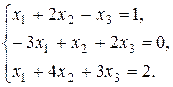
8. Решить систему методом Гаусса и Жордана-Гаусса: 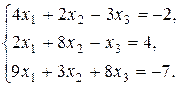
Вариант 4
1. Решить уравнение 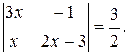
2. Решить систему 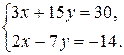
3. Вычислить 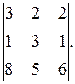
4. Решить систему по формулам Крамера: 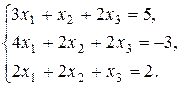
5. А = 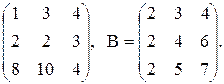 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 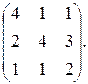 Найти матрицу
Найти матрицу 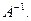 Показать, что АА
Показать, что АА  =Е.
=Е.
7. Решить систему матричным методом: 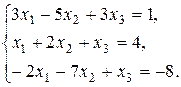
8. Решить систему методом Гаусса и Жордана - Гаусса: 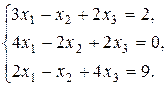
Вариант 5
1. Решить уравнение 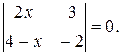
2. Решить систему 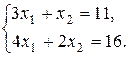
3. Вычислить 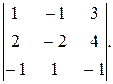
4. Решить систему по формулам Крамера: 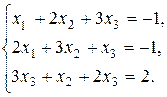
5. A = 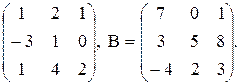 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 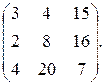 Найти матрицу А-1. Показать, что АА-1=Е.
Найти матрицу А-1. Показать, что АА-1=Е.
7. Решить систему матричным методом: 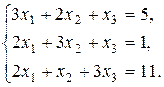
8. Решить систему методом Гаусса и Жордана-Гаусса: 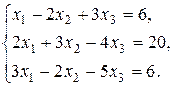
Вариант 6
1. Решить уравнение 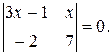
2. Решить систему 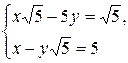
3. Вычислить 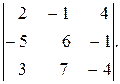
4. Решить систему по формулам Крамера: 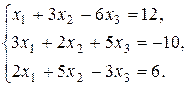
5. А = 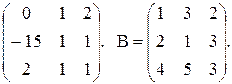 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 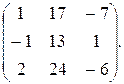 Найти матрицу А-1. Показать, что АА-1=Е.
Найти матрицу А-1. Показать, что АА-1=Е.
7. Решить систему матричным методом: 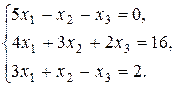
8. Решить систему методом Гаусса и Жордана - Гаусса: 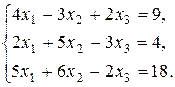
Вариант 7
1. Решить неравенство 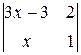 > 0.
> 0.
2. Решить систему 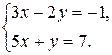
3. Вычислить 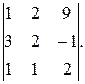
4. Решить систему по формулам Крамера: 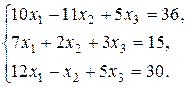
5. А = 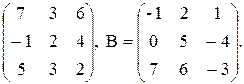 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 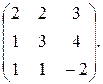 Найти матрицу А
Найти матрицу А 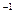 . Показать, что АА
. Показать, что АА 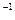 =Е.
=Е.
7. Решить систему матричным методом: 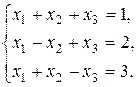
8. Решить систему методом Гаусса и Жордана - Гаусса: 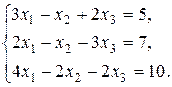
Вариант 8
1. Решить неравенство 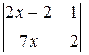 > 5.
> 5.
2. Решить систему 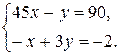
3. Вычислить определитель двумя способами: 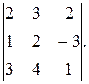
4. Решить систему по формулам Крамера: 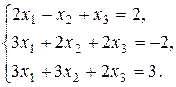
5. А = 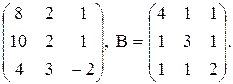 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 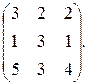 Найти матрицу А
Найти матрицу А 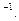 Показать, что АА
Показать, что АА 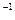 =Е.
=Е.
7. Решить систему матричным методом: 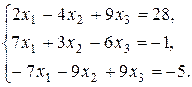
8. Решить систему методом Гаусса и Жордана - Гаусса: 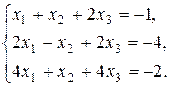
Вариант 9
1. Решить неравенство 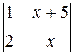 < 0.
< 0.
2. Решить систему 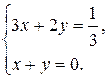
3. Вычислить определитель двумя способами: 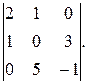
4. Решить систему по формулам Крамера: 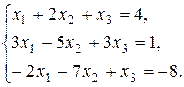
5. А = 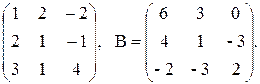 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 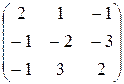 . Найти матрицу А/
. Найти матрицу А/ 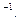 Показать, что АА
Показать, что АА 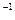 =Е.
=Е.
7. Решить систему матричным методом: 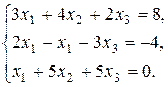
8. Решить систему методом Гаусса и Жордана - Гаусса: 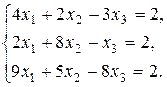
Вариант 10
1. Решить неравенство 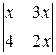 <14.
<14.
2. Решить систему 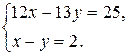
3. Вычислить 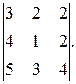
4. Решить систему по формулам Крамера: 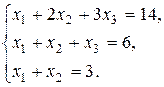
5. А = 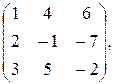 В =
В = 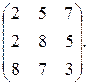 Найти АВ и ВА.
Найти АВ и ВА.
6. 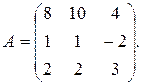 Найти матрицу А
Найти матрицу А 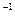 . Показать, что АА
. Показать, что АА 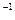 =Е.
=Е.
7. Решить систему матричным методом: 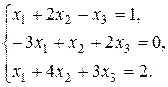
8. Решить систему методом Гаусса и Жордана - Гаусса: 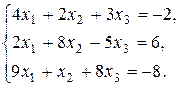
Вариант 16
1. Вычислить 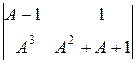 .
.
2. Решить систему 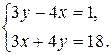
3. Вычислить 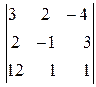 .
.
4. Решить систему по формулам Крамера:
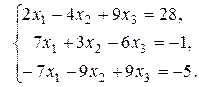
5. A = 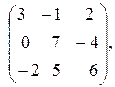 B =
B = 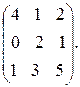 Найти АВ и ВА.
Найти АВ и ВА.
6. А = 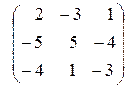 . Найти матрицу А
. Найти матрицу А 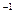 . Показать, что АА
. Показать, что АА 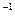 =Е.
=Е.
7. Решить систему матричным методом: 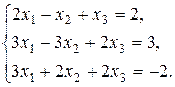
8. Решить систему методом Гаусса и Жордана – Гаусса:
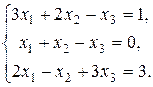
Вариант 17
1. Решить уравнение 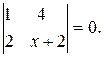


2. Решить систему 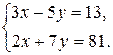
3. Вычислить 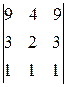 .
.
4. Решить систему по формулам Крамера:
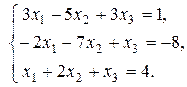
5. А = 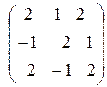 , В =
, В = 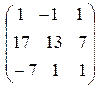 . Найти АВ и ВА.
. Найти АВ и ВА.
6. А = 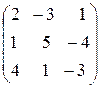 . Найти матрицу А
. Найти матрицу А 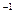 . Показать, что АА
. Показать, что АА 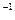 =Е.
=Е.
7. Решить систему матричным методом:
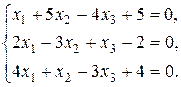
8. Решить систему методом Гаусса и Жордана – Гаусса: