Глава 1. Моделирование гармонического колебания для определения влияния его параметров.
Гармоническое колебание – основа всех существующих сигналов, характеризующееся тремя параметрами: амплитудой, частотой и начальной фазой.
U=Um*cos(wt+f), где Um - амплитуда, w - частота и f - фаза.
Задание: Заменив начальную фазу оператором FRAME проанализировать как влияет начальная фаза на спектр амплитуд. Посмотреть как меняется временная форма колебания.
|
|
|
|
|
|
Показатель степени, определяющее количество точек
Количество точек
Частота, на которой исследуется колебание
Амплитуда колебания
Начальная фаза
|
Выражение, описывающее временную форму колебания
Временная форма колебания
Преобразование Фурье
Спектр амплитуд
Спектр фаз, в котором появляется цифровой шум
Вывод: от изменения начальной фазы спектр амплитуд не меняется, так как временная форма сигнала независимо от фазы начальной остается синусоидальной, поэтому гармоника одна и она неизменна. Входная форма сигнала с изменением начальной фазы меняет начальную амплитуду.
Задание: В файле для гармонических колебаний добавить генератор случайных чисел и определить уровень шума N, при котором сигнал полностью забивается шумом.
|
|
|
Количество шумов
Временная форма сигнала с учетом шумов
Сигнал полностью поглощен шумами
|
В спектре амплитуд появляются дополнительный гармоники, которых не должно быть при сигнале без шумов
Глава 2. Исследование процесса амплитудного детектирования.
Амплитудная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда.
Детектирование – выделение полезного сигнала из модулированного. Процесс обратный модуляции.
Амплитудный детектор состоит из нелинейного элемента и из линейной части (фильтра нижних частот).
-Интервал времени
-Амплитуда сигнала
-Несущая высокочастотная частота
-Информационная низкочастотная частота
-Глубина модуляции
-Моделирование АМ сигнала
|
Входное напряжение
- преобразование Фурье
Спектр амплитуд
Нелинейное преобразование - возведение в квадрат.
|
|
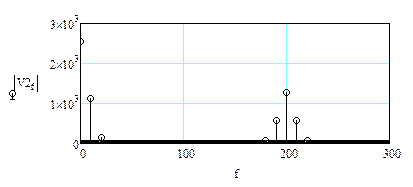
Спектр амплитуды после нелинейного преобразования - возведения в квадрат. Спектр обогатился.
|
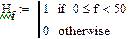
- фильтр нижних частот
|
|
-используем обратное преобразование Фурье
|
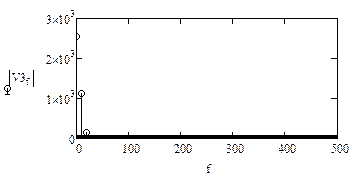
Спектр на выходе фильтра
|
Продетектированное колебание
Глава 3. Исследование влияния частотных фильтров полосовых на чистоту сигнала
Электрическим частотным фильтром называется линейный четырехполюсник, предназначенный для выделения из состава сложного входного воздействия частотных составляющих, расположенных в заданных диапазонах частот и подавление составляющих вне этого диапазона.
По взаимному расположению полос задерживания и пропускания фильтры делятся на ФНЧ, ФВЧ, инжекторные и полосовые
Показатель, от которого зависит количество точек
Начальная амплитуда
Исследуемая частота
Интервал времени
Преобразование Фурье
Интервал частот
Исходный импульсный радиосигнал
Спектр радиосигнала
Радиосигнал с шумами
Преобразование Фурье
Сигнал в канале связи при действии шумов
Его спектр амплитуд
Вставим полосовой фильтр, пропускающий полосу сигнала:
Соединяем сигнал с фильтром
Результат слияния сигнала с фильтром
Обратное преобразование Фурье
Возводим сигнал в квадрат, для получения полезного сигнала в нижних частотах
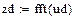Преобразование Фурье
Спектр амплитуд полученного сигнала
Возводим в квадрат сигнал с шумами
Преобразование Фурье
Спектр сигнала с шумами
Вставим ФНЧ для выделения полезного сигнала
Соединим ФНЧ с сигналом без шумов
Спектр полученного сигнала
Соединим ФНЧ с сигналом с шумами
Спектр сигнала с шумами
Обратное преобразование Фурье
Сигнал на выходе
Обратное преобразование Фурье
Сигнал на выходе с шумами
2. Вставим перед возведением в квадрат сигнала фильтр, пропускающий полосу:
Спектр сигнала с полосой
После аналогичных преобразований, рассмотренных выше, получим сигнал на выходе без шумов и с шумами соответственно:
Можно сделать вывод из представленного исследования, что выбирать фильтр надо учитывая тот факт, что полезный сигнал распределяется на всех частотах и выделяя полосу определенного диапазона надо быть готовым к тому, что либо недостаточный сигнал захватим, если диапазон слишком мал или сигнал будет слишком искажен, если диапазон настолько велик, что проникает слишком много шума.