Министерство образования и науки РФ
Рязанский институт (филиал)
Федерального государственного бюджетного
Образовательного учреждения
Высшего профессионального образования
«Московский государственный открытый университет
Им. В. С. Черномырдина »
Кафедра архитектуры и градостроительства
Г. С. Нечипорук
Решение задачи изгиба пластинки
С применением пк лира
Методические указания для
Студентов строительных специальностей
Рязань 2012
УДК 539.3
Н – 59
Г. С. Нечипорук
Решение задачи изгиба пластинки с применение ПК ЛИРА. Методические указания для студентов строительных специальностей. Рязанский институт (филиал) федерального государственного бюджетного образовательного учреждения «Московский государственный открытый университет им. В. С. Черномырдина», 2012
В методических указаниях дана постановка задачи изгиба жесткой пластинки. Приводится порядок решения указанной задачи с применением программного комплекса ЛИРА, реализующего метод конечных элементов. Приведены примеры по определению напряженно-деформированного состояния жесткой пластинки. Даны схемы и исходные данные для выполнения расчетно-графических работ.
Печатается по решению методического совета вуза
© Рязанский институт (филиал) МГОУ им. В. С. Черномырдина, 2012
© Г. С. Нечипорук
Оглавление
1) Изгиб прямоугольной пластинки. Краткие сведения из теории.. ……………..3
2) Решение задачи изгиба пластинки с применением ПК ЛИРА …..........………6
2.1 Режим запуска программы………………………………………………….6
2.2 Режим формирования расчетной схемы…………………………………..6
2.3 Режим - расчет задачи…………………………………………………..….8
2.4 Режим - анализ результатов расчета……………………………………….8
3) Другие условия опирания……………………………………………………….14
Приложение 1 – Задание для выполнения РГР 2. Расчет пластинки………….24
Изгиб прямоугольной пластинки.
Краткие сведения из теории
Основная и наиболее трудоемкая часть задачи расчета жесткой пластинки (рисунок 1) заключается в определении функции прогиба w (x,y) как решения бигармонического уравнения Софии Жермен (1), удовлетворяющего заданной нагрузке и условиям опирания пластинки.
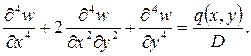 (1)
(1)
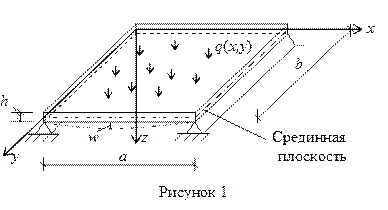
Здесь q (x,y) –поверхностная нагрузка на пластинку; 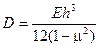 – цилиндрическая жесткость пластинки; h – толщина пластинки.
– цилиндрическая жесткость пластинки; h – толщина пластинки.
|
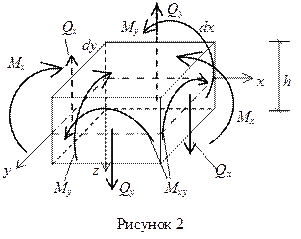
Внутренние усилия (рисунок 2) и, соответственно, напряжения в пластинке связаны с перемещениями следующими зависимостями.
Изгибающие моменты:
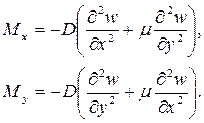 (2)
(2)
Крутящий момент:
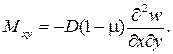 (3)
(3)
Поперечные силы:
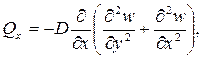
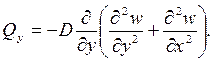 (4)
(4)
Согласно принятой в теории изгиба пластинок гипотезе Бернулли – Кирхгофа о жесткой нормали, напряжения, создающие изгибающие моменты Mx, My, определяются по формулам сопротивления материалов:
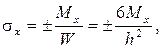
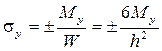 , (5)
, (5)
где: W = 1· h2 /6 – момент сопротивления элемента поперечного сечения пластинки единичной ширины.
Аналогично 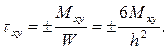 (6)
(6)
Таким образом, если известна функция w (x,y), то, вычислив максимальный прогиб, можно проверить для данной пластинки выполнение условия жесткости. w max ≤ [ w ].
Далее, определив внутренние усилия по выражениям (2) - (4), можно найти их максимальные значения и по формулам (5) и (6) вычислить наибольшие напряжения и дать оценку прочности пластинки.
Уравнение (1) имеет множество решений и для отыскания своего решения необходимо воспользоваться граничными условиями – условиями опирания пластинки.
Запись условий опирания.
В теории пластинок приняты три основных вида опирания – защемление, свободное (шарнирное) опирание и свободный неопертый край.
Пусть левый край пластинки 0-1 с координатами х = 0, 0 ≤ у ≤ b защемлен (рисунок 3). В этом случае граничные условия принимают вид:
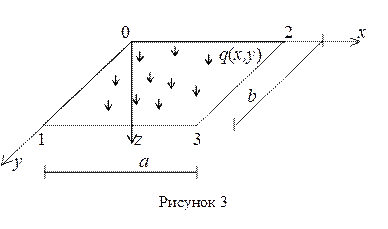
|
1) прогиб w = 0,
2) угол поворота левой грани 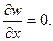
Если защемлены верхний или нижний края пластинки, условия опирания имеют аналогичные выражения:
1) прогиб w = 0, 2) угол поворота нижней (верхней) грани 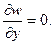
Представим, что верхний край 0 - 2 с координатами 0 ≤ x ≤ a, y = 0 шарнирно оперт. Тогда граничные условия записываются как:
1) прогиб w = 0,
2) Изгибающий момент на грани My = 0.
Поскольку производная по х на верхней опертой грани 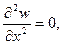 второе условие принимает вид:
второе условие принимает вид:
2) My = 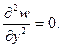
Если шарнирно оперты боковые грани, то условия опирания имеют вид:
1) w = 0, 2) Mx = 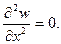
Пусть нижний край 1-3 (0 ≤ x ≤ a, y = b) неоперт. В этом случае w ≠ 0, а нулю должны быть равны усилия (реакции) на свободном неопертом крае. Т. е.
1) My = 0, 2) Mxy = 0, 3) Qy = 0.
Два последних условия можно объединить в одно 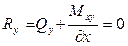 и граничные условия примут вид:
и граничные условия примут вид:
1) 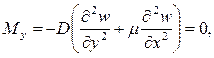
2) 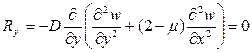 .
.
Если неоперты правый или левый край, то граничные условия запишутся как:
1) 
2) 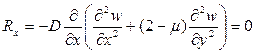 .
.
В связи с отсутствием общего решения дифференциального уравнения изгиба пластинки (1), разработаны и широко применяются методы численного интегрирования. Одним из них является метод конечного элемента (МКЭ). В этом случае пластинка разбивается на простейшие треугольные или четырехугольные элементы. Неизвестными являются линейные перемещения (прогибы) и угловые перемещения узловых точек элемента, которые определяются при решении системы линейных алгебраических уравнений, которая в матричной форме имеет вид:
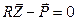 , (7)
, (7)
где R – матрица жесткости (реакций), 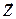 – вектор перемещений и
– вектор перемещений и 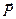 - вектор нагрузки.
- вектор нагрузки.
После определения перемещений находятся внутренние усилия.