Выйдя на режим «Результаты расчета» на экране появляется новое меню и схема пластинки с приложенной нагрузкой. Для получения вида изогнутой поверхности достаточно нажать на средней панели кнопу 
, в результате на экране изображается вид деформированной пластинки (рисунок 4).
Рисунок 5
|
Изополя прогибов получаем, используя кнопку 
«изополе прогибов». На экране слева появляются кнопки, обозначающие углы поворота элементов и прогибы узлов (рисунок 5). Для получения изополя прогибов необходимо активизировать кнопку 
. Изополе прогибов для нашей задачи приведено на рисунке 6.
Рисунок 6 – Изополе прогибов.
Изополе прогибов показывает, что наибольший прогиб имеет место в правом верхнем узле (№169) и составляет z = -5,016 мм.
На рисунках 7,8 показаны эпюры прогибов в горизонтальном и вертикальном сечениях. Получение эпюр описано в [1].
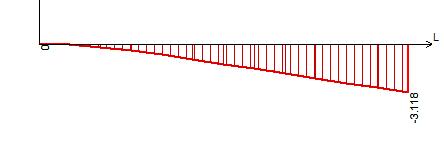
Рисунок 7 – Эпюра прогибов в сечении I- I
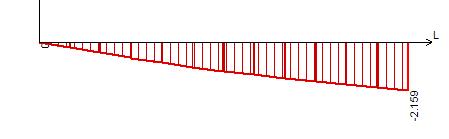
Рисунок 8 – Эпюра прогибов в сечении II- II
Для получения изополей моментов необходимо активизировать клавишу «Изополя напряжений» 
и в нижней части экрана появятся клавиши 
, соответствующие внутренним усилиям в жесткой пластинке. Ниже приводятся результаты расчета в виде изополей и эпюр внутренних усилий.
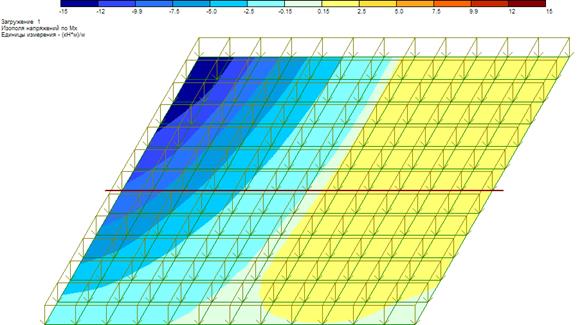
Рисунок 9 – Изополе моментов Мх
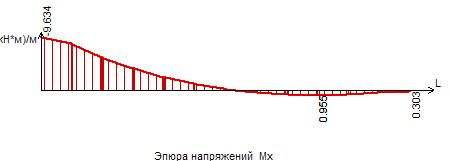
Рисунок 10 – Эпюра моментов Мх в сечении I-I
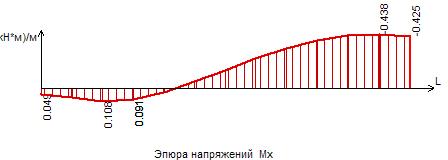
Рисунок 11 – Эпюра моментов Мх в сечении II-II
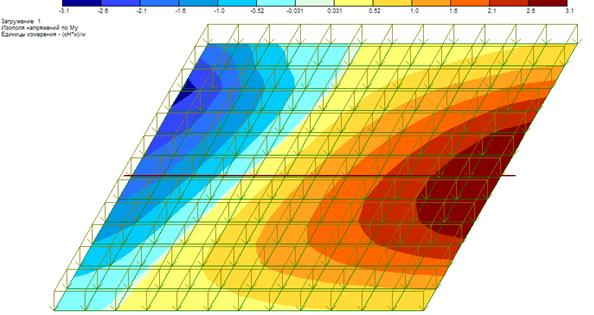
Рисунок 12 – Изополе моментов Му
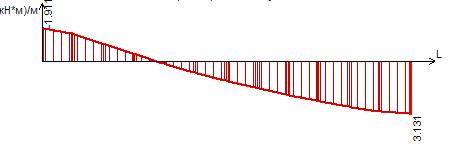
Рисунок 13 – Эпюра моментов Му в сечении I-I
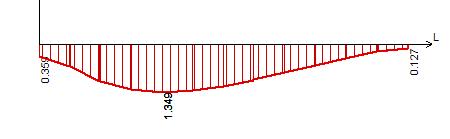
Рисунок 14 – Эпюра моментов Му в сечении II-II
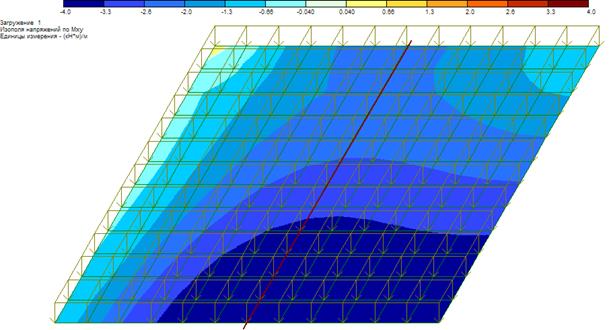
Рисунок 15 – Изополе моментов Мху
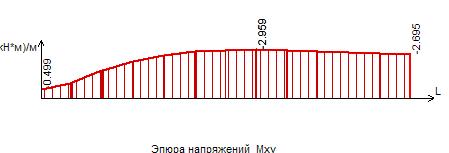
Рисунок 16 – Эпюра моментов Мху в сечении I-I
|
|
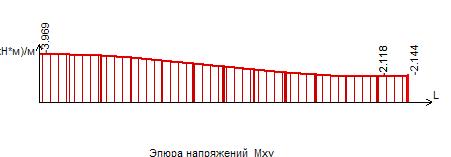
Рисунок 17 – Эпюра моментов Мху в сечении II-II
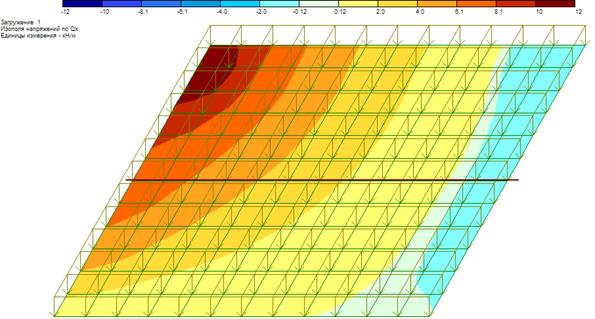
Рисунок 18 – Изополе поперечных сил Qх
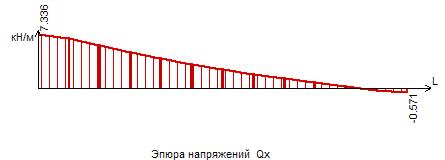
Рисунок 19 – Эпюра поперечных сил Qх в сечении I-I
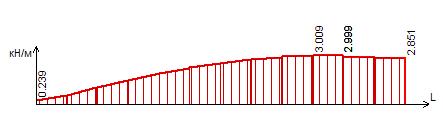
Рисунок 20 – Эпюра поперечных сил Qх в сечении II-II
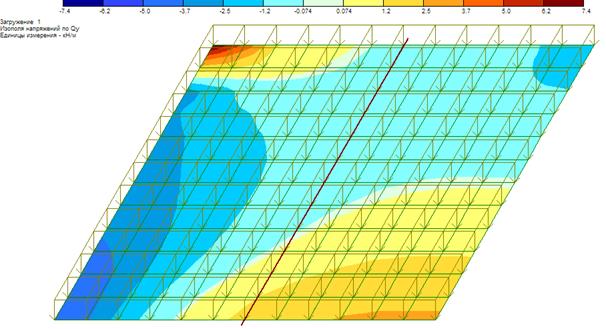
Рисунок 21 – Изополе поперечных сил Qу
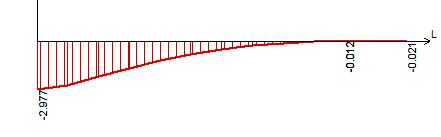
Рисунок 22 – Эпюра поперечных сил Qy в сечении I-I
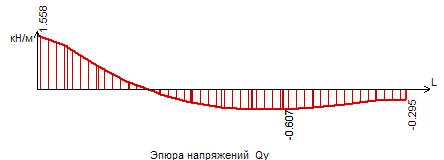
Рисунок 23 – Эпюра поперечных сил Qу в сечении II-II
Другие условия опирания
Теперь рассмотрим изгиб той же пластинки, когда в правом верхнем углу один узел (№141) оперт (рисунок 24).
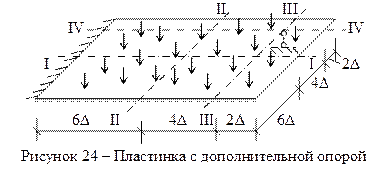
В связи с более сложными условиями опирания, напряженно-деформированное состояние пластинки будем рассматривать в четырех сечениях:
сечение I-I – горизонтальное сечение в середине пластинки.
сечение II-II – вертикальное сечение в середине пластинки.
сечение III-III – вертикальное сечение справа над дополнительной опорой - узлом 141.
сечение IV-IV – горизонтальное вверху пластинки (на расстоянии 2Δ от верхнего края, над дополнительной опорой).
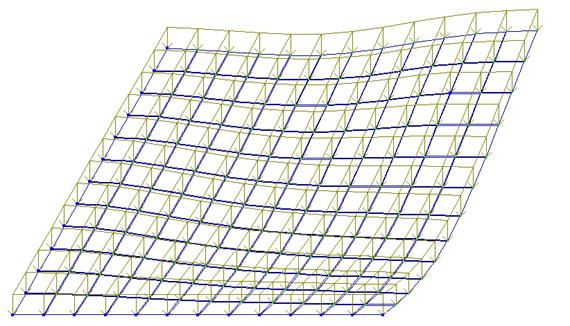
Рисунок 25 – Изогнутая поверхность пластинки
Вид изогнутой поверхности, показанной на рисунке 25, свидетельствует, что верхние слои пластинки растянуты не только у жесткой опоры слева, но и над промежуточной опорой в правом верхнем углу. Ниже это будет проиллюстрировано на изополях и эпюрах моментов и поперечных сил.
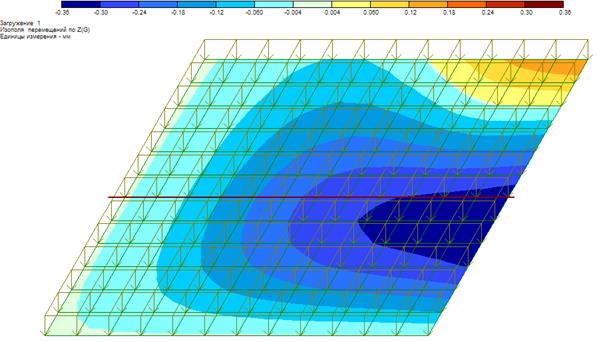
Рисунок 26 – Изополе прогибов
Изополе прогибов показывает, что наибольшие прогибы имеют место в зоне интенсивного синего цвета. Максимальный прогиб z = -0,357 мм в 78 узле (правый край пластинки). Правый верхний угол пластинки поднимается вверх (узел 169, z = 0.18мм).
|
|
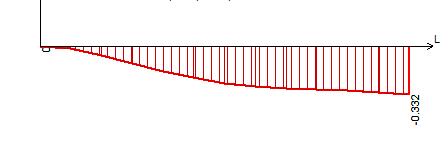
Рисунок 27 – Эпюра прогибов в сечении I-I
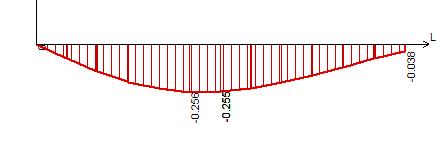
Рисунок 28 – Эпюра прогибов в сечении II-II
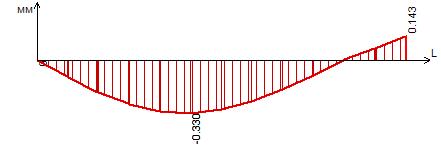
Рисунок 29 – Эпюра прогибов в сечении III-III
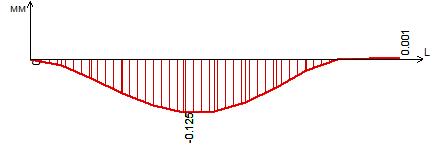
Рисунок 30 – Эпюра прогибов в сечении IV-IV
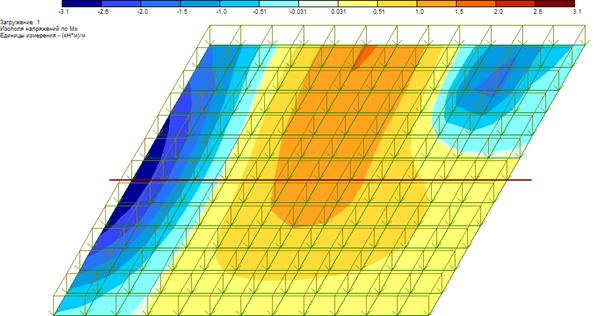
Рисунок 31 – Изополе моментов Мх
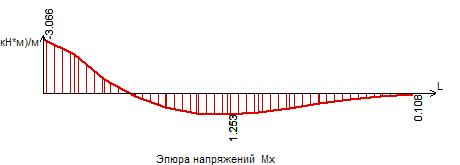
Рисунок 32 – Эпюра моментов Мх в сечении I-I
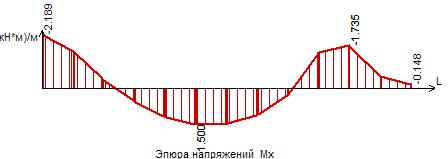
Рисунок 33 – Эпюра моментов Мх в сечении IV-IV
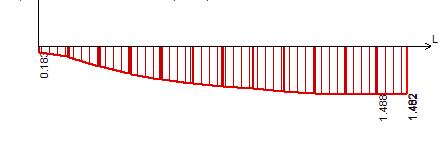
Рисунок 34 – Эпюра моментов Мх в сечении II-II
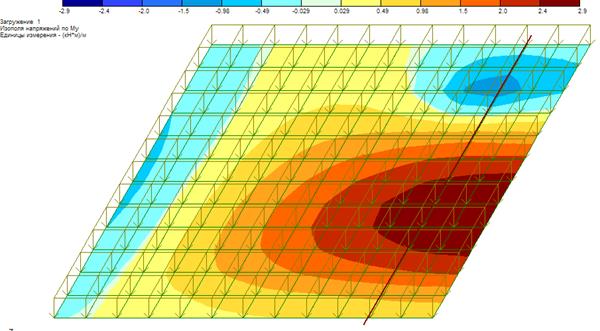
Рисунок 35 – Изополе моментов Му
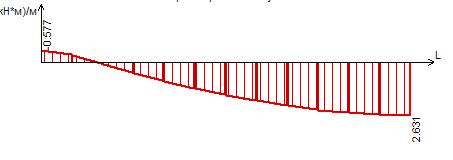
Рисунок 36 – Эпюра моментов Му в сечении I-I
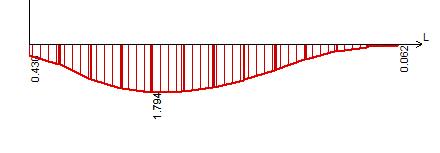
Рисунок 37 – Эпюра моментов Му в сечении II-II
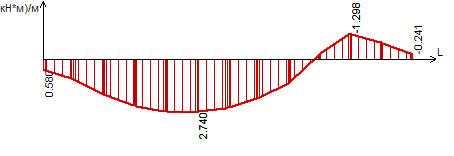
Рисунок 38 – Эпюра моментов Му в сечении III-III
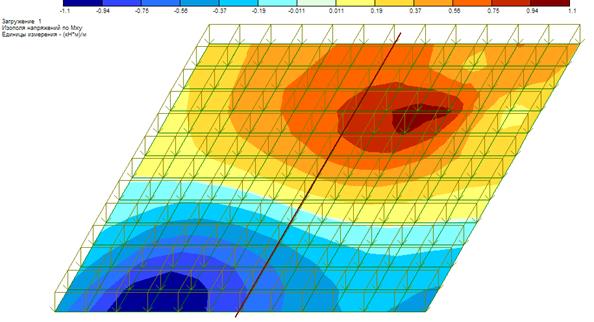
Рисунок 39 – Изополе моментов Мху
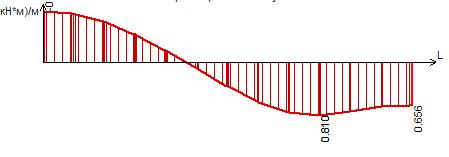
Рисунок 40 – Эпюра моментов Мху в сечении II-II
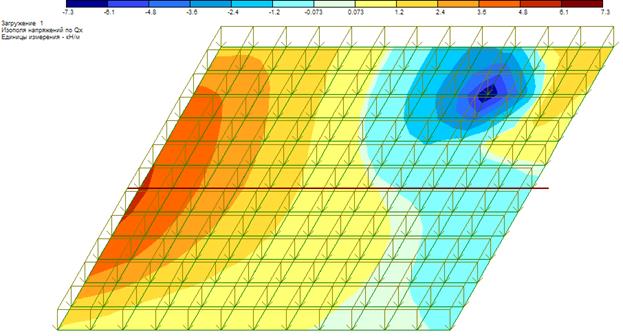
Рисунок 41 – Изополе поперечных сил Qx
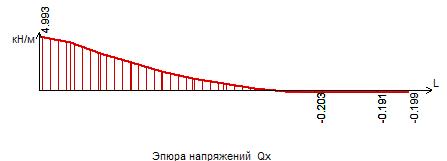
Рисунок 42 – Эпюра поперечных сил Qx в сечении I-I
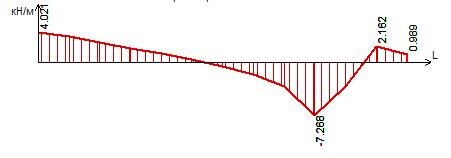
Рисунок 43 – Эпюра поперечных сил Qx в сечении IV-IV
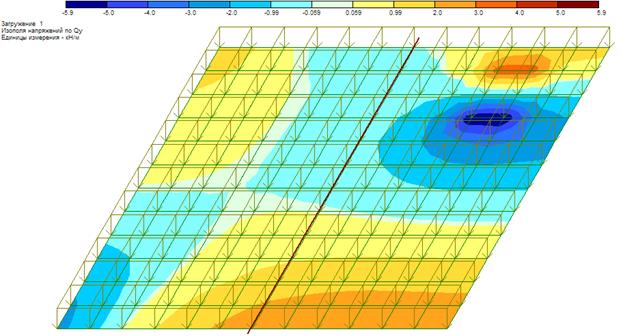
Рисунок 44 – Изополе поперечных сил Qу
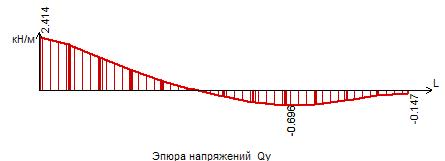
Рисунок 45 – Эпюра поперечных сил Qу в сечении II-II
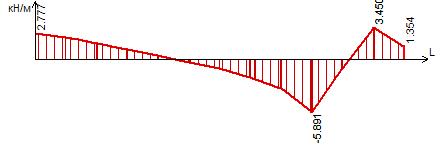
Рисунок 46 – Эпюра поперечных сил Qу в сечении III-III
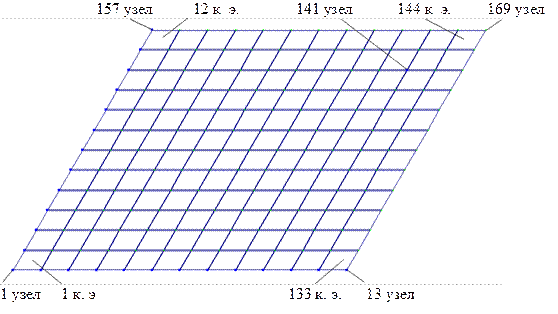
Рисунок 47– Нумерации узлов и конечных элементов задачи
Ниже, в таблице 1 показано как изменились прогибы и внутренние усилия при изменении условий опирания пластинки.
Дополнительная опора привела к заметному (в разы) снижению прогибов и изгибающих моментов. Значения наибольших поперечных сил изменились незначительно.
Таблица 1
| Пластинка без дополнительной опоры | Пластинка с опорой в 141 узле | |
| z (max), мм | - 5,01 (узел 169) | -0,357 (узел 78) |
| Mx, кНм/м | -14,92 (12 к. э.) | -3,07 (6 к. э.) |
| Mу, кНм/м | 3,16 (11 к. э.) | 2,99 (139 к. э.) |
| Mxу, кНм/м | -3,95 (61 к. э.) | -1,13 (25 к. э.) |
| Qx кн/м | 13,37 (11 к. э.) | -10,13 (119 к. э.) |
| Qу кн/м | 7,44 (12 к. э.) | -13,1 (118 к. э.) |
|
|
Задание для РГР №2
«Расчет пластинки на изгиб»
Для заданной прямоугольной пластинки с размерами а х б (рисунок 1) необходимо провести анализ напряженно-деформированного состояния (НДС) с использованием ПК ЛИРА.
Для этого следует:
1) получить деформированный вид пластинки, изополе прогибов «z » и определить наибольший прогиб,
2) получить изополя внутренних усилий (Мх, Му, Мху , Qx, Qy) с определением элементов в которых возникают наибольшие усилия, и самих наибольших внутренних усилий,
3) построить эпюры прогибов и внутренних усилий в сечениях I-I и II-II,
4) дать заключение об НДС заданной пластинки.
В расчетах принять: материал бетон (Е = 2∙104МПа, μ = 0,25), толщина пластинки h = 16 см.
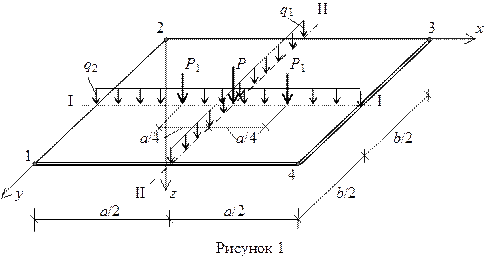
Расчет пластинки провести для трех случаев опирания:
1) все края пластинки свободно оперты,
2) все края пластинки защемлены,
3) пластинка опирается в углах (точки 1, 2, 3 и 4).
Размеры и нагрузку взять из таблицы 1 по шифру студента (две последние цифры номера зачетной книжки).
При выборе шага сетки (размеров конечного элемента) необходимо, что бы на короткой стороне пластинки было не менее 10 элементов.
Таблица 1
| Номер строки | P, кН | P 1, кН | q 1, кН/м | q 2, кН/м | а, м | б, м |
| 3,2 | 3,84 | |||||
| 4,32 | 3,6 | |||||
| 4,2 | 3,0 | |||||
| 3,0 | 4,8 | |||||
| 3,2 | 4,48 | |||||
| 3,0 | 4,5 | |||||
| 4,8 | 3,2 | |||||
| 4,5 | 3,0 | |||||
| 5,04 | 3,6 | |||||
| 3,6 | 4,32 | |||||
| Вторая цифра шифра | Первая цифра шифра |
Учебное издание
Нечипорук Геннадий Савельевич