Ниже рассматриваются практические методы оценки основных статистических характеристик измеряемых величин: математических ожиданий, их корреляционных и взаимно-корреляционных функций.
Одним из основных вопросов, связанных с вычислением оценок статистических характеристик случайных стационарных эргодических процессов по их реализациям, является вопрос точности получаемых оценок. Как известно, точность оценки зависит от длины используемых реализаций случайных процессов и частоты съема данных с них, однако количественная мера этой зависимости может быть получена в общем виде лишь при априорном знании корреляционной (взаимно-корреляционной) функции процесса, что практически не может иметь место. В то же время для практического использования необходимо заранее, до вычислений оценок статистических характеристик процессов, уметь хотя бы приближенно оценивать параметры реализации, дающие требуемую точность оценок, т. е. определять основные характеристики эксперимента, проводимого на объекте контроля. Важность решения этих вопросов привела к появлению ряда работ, в которых при определенных ограничениях на структуру статистических характеристик даются рекомендации по выбору параметров реализации [104, 105, 106].
Описываемый ниже метод оценки параметров реализации [52, 107] характеризуется достаточной по практическим приложениям широтой класса исследуемых корреляционных и взаимно-корреляционных функций и простотой оценки основных параметров опыта на объекте: значений длин реализации процесса и частоты съема данных с них. Кроме обычных ограничений, накладываемых в книге на класс случайных процессов, представляющих собой изменения измеряемых величин во времени, будем считать их близкими к нормальным по закону распределения.
а) Оценка математического ожидания
Как известно [108], при расчете оценки математического ожидания mх по непрерывной реализации случайного процесса x(t)
(1.40)
где T-длина реализации процесса, средняя квадратичная погрешность расчета определяется формулой
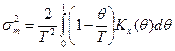(1.41)
где Rx(θ)—значение корреляционной функции процесса x(t) при аргументе θ.
При расчете оценки математического ожидания по дискретному ряду точек реализации случайного процесса
(1.42)
где to — расстояние между соседними точками реализации процесса;
N- общее число точек реализации (N = T/τ0).
(1.43)
Средняя квадратичная погрешность
Следовательно, для конкретной оценки погрешности расчета математического ожидания необходимо знание корреляционной функции процесса.
Графики вычисленных оценок корреляционных функций измеряемых величин рассматриваемого класса в большинстве случаев носят монотонно убывающий характер и хорошо аппроксимируються линейной комбинацией (суммой) экспонент при всех значениях аргумента, за исключением самих хвостов корреляционных функций, которые в силу неточности оценки вообще недостоверны. Исключением являются процессы, в которых проявляются периодические колебания. В этих случаях аппроксимация кривой комбинацией экспонент справедлива лишь для начального участка корреляционной функции и может быть принята, если для дальнейших расчетов используется лишь эта часть корреляционной функции, либо если можно ограничиться наиболее грубой аппроксимацией. Во всех указанных случаях, учитывая реальные точности работы датчиков и практически возможные длины реализаций, целесообразно ограничить число слагаемых экспонент в аппроксимации тремя, т. е. считать, что структура искомой корреляционной функции может быть представлена лишь следующим выражением:
(1.44)
где αi и αi (при i=1, 2, 3) —неизвестные параметры корреляционной функции.
Выражение (1.44) может быть несколько уточнено и классифицировано за счет соображений, общих для изучаемых процессов. При простейшей самой грубой аппроксимации α2 = α3 = ∞ пренебрегают дифференцируемостью случайного процесса и ищут оценку корреляционной функции в виде
(1.45)
где Dx — дисперсия случайного процесса, α = α1.
Значительно более точная аппроксимация может быть достигнута с помощью комбинации двух экспонент (α3 = ∞). В этом случае уже возможен учет свойства дифференцируемое случайного процесса, которое обычно имеет место на практике, поскольку почта любая измеряемая величина находится на выходе какого-либо динамического звена. При учете Дифференцируемости значение корреляционной функции при нулевом аргументе должно удовлетворять ранее отмеченным условиям:
(1.46)
Ввиду этого корреляционная функция, состоящая из комбинации двух экспонент, может иметь только следующий вид:
при β > α (1.47)
или
при β = α (1.48)
где α=α1 и β= α2.
Наконец, линейная комбинация из трех экспонент, удовлетворяющая, условиям дифференцируемости, представляет собой следующие выражения:
при γ>β>α (1.49)
или
при γ = β = α (1.50)
где γ=α2.
На рис. 1.9 представлены кривые зависимости нормированной корреляционной функции rx(τ)=Kx(τ)/Dx от ατ при различным значениях β/α и γ/α, полученные по формулам (1.45),(1.47)-(1.50). На графике (рис. 1.9) очерчена область, в которой располагаются рассмотренные корреляционные функции. На начальном этапе планирования эксперимента на объекте априорное знание даже структуры корреляционной функции невозможно, поэтому целесообразно задаться такой ее структурой, чтобы она была достаточно близка к любой конкретной Rx(τ), лежащей внутри возможной области нахождения рассмотренных корреляционных функций, очерченной на рис. 1.9. Такая функция, с которой в дальнейшем и производится анализ погрешностей, будет называться эталонной корреляционной функцией (Rэ(τ)). В качестве Rэ(τ) целесообразно выбрать структуру, находящуюся примерно в середине возможного очерченного на рис. 1.9 диапазона. Она имеет вид (1.47) при соотношении показателей экспонент β/α = 1,5, т. е. нормированная эталонная корреляционная функция определяется выражением.
(1.51)
где α- неизвестный параметр, который должен быть определен непосредственно по реализации изучаемого случайного процесса.
Таким образом, задача определения корреляционной функции процесса для расчета погрешностей оценок статистических характеристик сведена к задаче определения одного параметра α. На рассматриваемой стадии изучения процесса этот параметр должен быть найден достаточно простым анализом имеющейся реализации процесса.
Известно, что для этого можно воспользоваться формулой, связывающей в случае нормального стационарного дифференцируемого процессе среднее число нулей в единицу времени n0 (т. е. среднее число пересечений реализацией процесса его математическою ожидания за единицу времени) и вторую производную нормированной корреляционной функции rx(τ)
(1.52)
В нашем случае r" x(τ) определяется дифференцированием формулы аппроксимации (1.51)
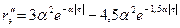
Подставив в исходную формулу (1.52) полученное выражение г"э(0), получим:
или
(1.53)
Непосредственная достаточно хорошая оценка значений n0 может быть получена во многих случаях по сравнительно небольшой длине реализации, включающей 20—40 нулей.
Существенно отметить невысокую чувствительность метода к ошибкам оценки па. Таким образом, возникает возможность определения погрешности расчета оценки математического ожидания путем подсчета.по начальному интервалу реализация случайного процесса среднего числа нулей в единицу времени. Для использования указанной методики выразим относительную среднюю квадратичную погрешность оценки математического ожидания ηm=σm/√Dx через определяемый по реализации параметр α путем подстановки в формулы (1.41) и (1.43) эталонной корреляционной функции (1.51),
В случае расчета оценки математического ожидания по непрерывной реализации процесса
(1.54)
В случае расчета по дискретному ряду точек реализации
(1.55)
На рис. 1.10 приведены построенные по формулам (1.54), (1.55) зависимости относительной погрешности от искомых параметров эксперимента: длины реализации и частоты съема данных. Эти кривые, так же как и формулы (1.54) и (1.55), могут использоваться для определений искомых параметров опыта по заданному относительному значению погрешности оценки математического ожидания.
б) Оценка корреляционной функции
Расчет оценки корреляционной функции случайного процесса при непрерывном съеме данных с реализации производится по формуле
(1.56)
Средняя квадратичная погрешность определения корреляционной функции рассматриваемого класса процессов при непрерывном съеме данные может быть вычислена по следующей формуле [108] (погрешностью оценки математического ожидания пренебрегаем):
(1.57)
При дискретном съеме данных с реализации случайного процесса
(1.58)
где n=τN/T, N = T/t0, формула погрешности определения оценки корреляционной функции приобретает вид:
(1.59)
Для определения искомых параметров эксперимента (T,t0) по заданному значению относительной средней квадратичной погрешности оценки корреляционной функции rRx(τ) = σR(τ)/Rx(τ) воспользуйся выбранной структурой эталонной корреляционной функции rэ(τ) (1.51). Для нее на рис. 1.11 даны рассчитанные по формулам (1.57) и (1.59) зависимости ηRэ(τ) от α(τ), αT и αt0. Учитывая достаточно простую форму полученных зависимостей, но весьма сложную структуру исходных формул (1.57) и (1.59), представляется целесообразным использовать в рекомендуемой методике вместо исходных формул приближенные существенно упрощенные зависимости. ηkэ = f(αt0, αT, ατ)
Полученные кривые приближенно (погрешность аппроксимации не превышает 6,5%) описываются следующей формулой:
(1.60)
где С и p-функции αТ, показанные на рис. 3-7.
По формуле (3-41) можно определить, рассчитав по реализации значение α и задаваясь T в t0, точность оценки вычисляемых точек корреляционной функции при условии, что она имеет вид эталонной кривой (β/α=1,5). Точность оценок остальных точек корреляционной функции всегда несколько ниже за счет погрешности интерполяции. Эта добавочная составляющая погрешности подробно рассмотрена в [104].
При любом другом виде корреляционной функции rx(τ) из области рис. 1.9, т. е при изменении параметров аппроксимации β/α и γ/α относительно эталонной корреляционной функции и при одних и тех же значениях T, τ и t0 погрешность оценки корреляционной функции также изменяется. Однако относительные погрешности
во всем принятом диапазоне изменения β/α и γ/α, как показали расчеты, мало зависят от параметров Т и t0.
На рис. 3-8 показана область изменения ξ при τ=0 и при различных β/α для следующих диапазонов изменения остальных параметров:
γ/α = 1 ÷ ∞; αt0 = 0 ÷ 2; αT = 10 ÷ 120.
С увеличением значений γ/α модуль ξ также несколько увеличивается, при увеличении αt0 а модуль ξ уменьшается внутри очерченной области. Таким образом, возникает возможность применения следующей методики при расчете оценки корреляционной функции случайного стационарного процесса;
1) подчитывается по реализации процесса среднее число нулей в единицу времени n0 и рассчитывается α по формуле (1.53);
2) по заданной ηRx(τ) в любой точке корреляционной функции определяются искомые значения параметров реализации Т и t0 по формуле (1.60);
3) посла построения оценки корреляционной функции и аппроксимации ее (например, методом Симою [109]) определяется ξ по кривым рис. 1-12;
4) оценивается действительная погрешность ηRx(τ), получившаяся в данном конкретном случае:
(1.61)