КООПЕРАТИВНЫЕ (КОАЛИЦИОННЫЕ) ИГРЫ.

НЕАНТАГОНИСТИЧЕСКИЕ ИГРЫ.

В этих играх, в отличие от антагонистических игр, интересы игроков не взаимно противоположные, а лишь пересекаются. Здесь существует большое множество взаимовыгодных ситуаций, приводящих игроков к образованию коалиций для увеличения выигрыша. Такие игры называются коалиционными или кооперативными. Если в правилах игры коалиции запрещены, то соответственно такие игры называются бескоалиционными. Формально для n игроков такие игры можно представить следующим образом:

Система Г= 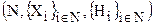, где N= – множество игроков, X_i – множество стратегий игрока i, Н_i – функция выигрыша игрока i, определённая на декартовом произведении множеств стратегий всех игроков: 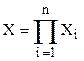- (множество ситуаций игры), называется бескоалиционной игрой.

Для двух игроков такие игры называются биматричными и определяются системой: Г=(Х₁, X₂, Н₁, Н₂), Х= Х₁´Х₂. Если количество чистых стратегий у игроков 1 и 2 соответственно m и n, то

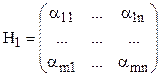и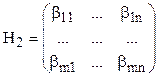

Ранее были рассмотрены два примера биматричных игр: пример 1(два бандита) и пример 2(семейный спор)..Напомним их матрицы: для примера 1:

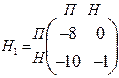и .

Для примера 2: 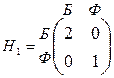и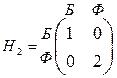

Для бескоалиционных игр для n игроков ранее также давалось определение ситуации равновесия по Нэшу: ситуация 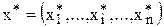будет ситуацией равновесия по Нэшу, если для любого игрока, т.е. и любой его стратегии, т.е. 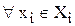Þ , т.е. замена оптимальной стратегии i -го игрока в ситуации 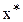на любую его другую стратегию 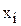не может увеличить его выигрыш .

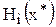Внимательный анализ данного определения приводит к выводу о том, что i -му игроку невыгодно менять свою оптимальную стратегию на любую его другую стратегию 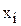, только в том случае, если остальные игроки придерживаются своих оптимальных стратегий, входящих в оптимальную ситуацию .

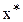Следовательно, согласно данному определению: 1) не следует трактовать как оптимальную стратегию для i -го игрока. Она является оптимальной только для всего набора оптимальных стратегий, входящих в состав ситуации 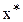. 2) нет отрицания того, что отклонение от ситуации равновесия не одного, а двух и более игроков может привести к увеличению выигрыша хотя бы у одного из отклонившихся игроков, что является побуждением к возможности образования коалиций, для которых существуют возможности увеличения своих выигрышей.

В примере 1 ситуацией равновесия по Нэшу, как было показано ранее, является ситуация (П,П), когда Н₁(П,П)= Н₂(П,П)= –8. Но если два бандита вступят в коалицию и оба поменяют по договорённости свои оптимальные стратегии по Нэшу на ситуацию (Н,Н), то оба окажутся в выигрыше, когда Н₁(Н,Н)= Н₂(Н,Н)=–1.

КООПЕРАТИВНЫЕ (КОАЛИЦИОННЫЕ) ИГРЫ.

В теории кооперативных (коалиционных) игр основной единицей анализа является группа игроков (коалиция). Цель анализа – определить такие варианты объединения, которые будут наиболее полезны по распределению выигрыша внутри коалиции и вопросы устойчивости таких коалиций.

Формализуем анализ: пусть N – множество игроков. SÍN – некоторое подмножество (коалиция) всего множества игроков. Заметим, что минимальной коалицией в таких объединениях является любой один игрок, а максимальной коалицией является договорённость всех n игроков.

- ситуация в игре Г. Через х|| обозначим факт замены в ситуации х коалиционной подситуации х_s из игроков множества SÍN на любую другую коалиционную их подситуацию . Из примера 1 следует, что, если х* ситуация равновесия по Нэшу, то не всегда Þ (1).

Примеры таких нарушений: Н_i(П,П)= –8, Н_i(Н,Н)=–1, т.е. 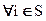коалиции из двух бандитов имеем-8< -1, или Н₁(П,Н) = Н₂(Н,П)= –1, а это также больше,чем -8.

Поэтому рождается новое определение равновесия, для которого условие (1) выполняется всегда.

Определение. Ситуация х* называется сильно равновесной, если для любой коалиции, т.е. "SÍN и любой коалиционной подситуации, т.е. 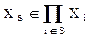Þ

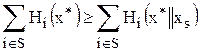(2).

Это определение гарантирует нецелесообразность образования коалиций между игроками.

Несложно заметить, что любая сильно равновесная ситуация является ситуацией равновесия по Нэшу, так как условие сильного равновесия (2) справедливо для любой коалиции, в том числе для коалиций из одного игрока. Следовательно, условие равновесия по Нэшу является необходимым условием сильного равновесия, как частный случай коалиций, состоящих из одного игрока. Однако сильное равновесие существует очень редко.

Сильно равновесной ситуацией в примере 2 (семейный спор) являются обе ситуации равновесия по Нэшу (Б,Б) и (Ф,Ф), о которых говорилось ранее. Действительно для коалиции из мужа и жены имеем: Н₁(Б,Б)+Н₂(Б,Б)=2+1=3 = Н₁(Ф,Ф)+Н₂(Ф,Ф)=1+2=3, что Н₁(Б,Ф)+Н₂(Б,Ф)=0+0=0 = Н₁(Ф,Б) + Н₂(Ф,Б)=0+0=0.

Помимо указанных принципов оптимальности существует также принцип оптимальности по Парето:

Определение: Ситуация ÎХ называется оптимальной по Парето в игре Г, если не существует такой ситуации хÎХ, для которой выполнялись бы следующие условия: 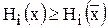" iÎN и 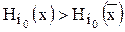хотя бы для одного i₀ÎN.

Множество всех ситуаций оптимальных по Парето в игре Г обозначим Х^р.

Из определения следует: если Î Х^р, то не существует другой ситуации хÎХ, которая была бы предпочтительнее для всех игроков или, выражаясь другими словами, не существует другой такой ситуации хÎХ, когда бы, как минимум, один окажется в выигрыше, а остальные игроки не проиграют.

Имеем следующее содержательное отличие ситуации равновесия по Нэшу от ситуации оптимальной по Парето: для первой ситуации ни один игрок, действуя в одиночку, не может увеличить свой выигрыш, для второй ситуации все игроки, действуя совместно, не могут увеличить выигрыш каждого. Также для второй ситуации «отклонившийся» игрок может увеличить свой выигрыш за счёт проигрыша некоторых других игроков (или проигрыша другого игрока).

Также несложно заметить, что любая сильно равновесная ситуация является ситуацией оптимальной по Парето, так как для сильного равновесия условие оптимальности по Парето является необходимым условием как частный случай коалиций, состоящих из всех игроков, т.е. сильно равновесная ситуация х* является оптимальной по Парето, так как и для коалиции из всех игроков выполняется условие (2) в виде: 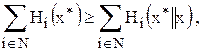где хÎХ ситуации для коалиции из всех игроков, говорит о невозможности улучшения выигрыша при смене ситуации х* на любую другую.

В примере 1 ситуация (Н,Н), когда Н₁(Н,Н)= Н₂(Н,Н)= –1, является оптимальной по Парето, так как отклонение от этой ситуации не приведёт, как минимум, к выигрышу хотя бы у одного из игроков при не проигрыше у другого игрока. Так для ситуации (П,П), когда Н₁(П,П)= Н₂(П,П)= –8, что меньше -1 в ситуации (Н,Н), говорит об одновременном проигрыше двух игроков, для ситуаций (П,Н) и (Н,П) или, соответственно, второй игрок проигрывает, так как Н₂(П,Н)= –10<-1., или первый, так как Н₁(Н,П)= –10<-1. При этом, если один из игроков поменяет свою стратегию с Н на П, то, соответственно, или первый, или второй игрок окажется в выигрыше, так как Н₁(П,Н)= Н₂(Н,П)= 0, что больше -1.

Сильно равновесные ситуации в примере 2 (Б,Б) и (Ф,Ф) являются и оптимальными по Парето, так как смена этих ситуаций у игроков на другие не приведёт, как минимум, к выигрышу хотя бы у одного из игроков при не проигрыше у другого игрока. Так замена ситуации (Б,Б) на ситуацию (Ф,Ф) и наоборот, приводит соответственно к проигрышу жены, а, если наоборот, то проигрышу мужа. Так Н₁(Б,Б)=2 Н₁(Ф,Ф)=1 говорит о проигрыше жены при замене ситуации (Б,Б) на ситуацию (Ф,Ф), и Н₂(Ф,Ф)=2>Н₂(Б,Б)=1 говорит о проигрыше мужа при замене ситуации (Ф,Ф) на ситуацию (Б,Б). Также замена ситуаций (Б,Б) и (Ф,Ф) на ситуации (Б,Ф) или (Ф,Б) приведёт к проигрышу и мужа и жены, так как Н₁(Б,Ф)=Н₂(Б,Ф)=Н₁(Ф,Б)=Н₂(Ф,Б)=0, что меньше 1 или 2.