Формирование понятия«энергия»
Формирование понятия «энергия» осуществляют с опорой на знания учащихся о механической работе и мощности. Начинать формировать это понятие лучше с опытов. Например, поднять над столом гирю. Обратить внимание учащихся на то, что гиря не движется, следовательно, работа не совершается. Но если гиря начнет падать, то она может произвести определенное действие, т.е. совершить работу. Для подтверждения этого можно поставить опыт, в котором падающий груз приводит в движение тело. Или в следующем опыте показать сжатую пружину, которая, распрямляясь, толкает шарик, тележку или поднимает груз, совершая при этом работу. Сделать вывод: поднятый на некоторую высоту груз и сжатая пружина обладают способностью совершать работу. Или на наклонном желобе установить небольшой деревянный цилиндр; стальной шарик, скатившись сверху, ударяет о цилиндр и передвигает его.
Если тело или несколько взаимодействующих между собой тел обладают способностью совершить работу, то принято говорить, что они обладают энергией. Поэтому можно сказать, что поднятая гиря, сжатая пружина, движущийся шарик обладают энергией.
Энергия есть особая физическая величина, характеризующая способность тела (или нескольких тел) совершать работу. Тело только тогда может совершить работу, когда оно обладает энергией. Чем большую работу может совершить тело, тем большей энергией оно обладает. Поэтому энергию можно рассматривать как своего рода «запас» возможной (еще не совершенной) работы. В результате совершенной работы тело переходит из одного состояния в другое: гиря опускается, сжатая пружина распрямляется, скорость движущегося шарика уменьшается, при этом энергия этих тел изменяется. Мерой изменения энергии при переходе тела из одного состояния в другое является совершенная им работа.
Дальнейшим этапом в формировании понятия «энергия» является рассмотрение двух основных видов механической энергии − кинетической и потенциальной.
Понятие «кинетическая энергия»
Можно начать с примеров движущихся тел, затем сообщить, что каждому движущемуся телу приписывают особую характеристику – кинетическую энергию.
В физике энергию движущегося тела называют кинетической (от греч. kinetikos – приводящий в движение). Кинетическая энергия обозначается буквой К (или Е К) и измеряется в СИ в тех же единицах, что и работа, т.е. в джоулях.
За кинетическую энергию тела принимают величину, равную работе, произведенной при разгоне тела из состояния покоя до данной скорости или величину, равную работе силы, необходимой для остановки данного тела. После этого записывают формулу для расчета кинетической энергии
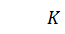 (4.8)
(4.8)
Кинетическая энергия прямо пропорциональна массе тела и квадрату скорости его движения.
Важно обратить внимание учащихся на то, что кинетическая энергия тела зависит от того, относительно каких тел рассматриваем движение. Кинетическая энергия является разностной величиной.
Подвести итоги рассмотрения связи между изменением кинетической энергии тела и работой сил, приложенных к нему, можно, используя таблицу 4.1.
Таблица 4.1
Связь механической работы и кинетической энергии
| № п/п | Направление силы, действующей на тело и направление движения | Работа | Модуль скорости | Кинетическая энергия |
| Совпадают |  ,
положительная ,
положительная
| Возрастает | Возрастает Δ К = А | |
| Противоположны | 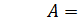 ,
отрицательная ,
отрицательная
| Убывает | Убывает Δ К = А | |
| Взаимно перпендикулярны | А = 0 | Не изменяется | Не изменяется, Δ К = 0 | |
| Сила действует на покоящееся тело | (F 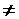 0, s = 0) 0, s = 0)
| Не изменяется | Не изменяется, Δ К =0 | |
| Тело движется по инерции | А =0
(F = 0, s 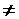 0) 0)
| Не изменяется | Не изменяется, Δ К = 0 |
Понятие «потенциальная энергия»
Рассмотрение понятия «потенциальная энергия» можно также начать с примера.
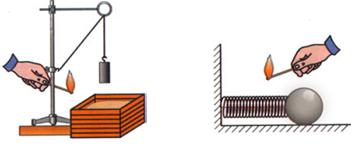 |
Целесообразно провести два несложных опыта. В первом – поднимаем и укрепляем на нити над ящиком с песком гирю (рисунок 4.3, а). Во втором — между упором и шариком помещаем предварительно сжатую и связанную ниткой пружину (рисунок 4.3, б).
а б
Рисунок 4.3
Оба тела (гиря и пружина) неподвижны (υ = 0) и не обладают кинетической энергией. Но и у гири, и у пружины есть возможность совершить работу. Для этого достаточно в обоих случаях пережечь нить! В физике говорят, что тела (поднятая гиря, взаимодействующая с Землей и сжатая пружина) обладают потенциальнойэнергией (от лат. potentia – скрытая способность).Потенциальную энергию в СИ измеряют в тех же единицах, что и работу, – в джоулях. Обозначается потенциальная энергия буквой П (или Е П).
Учащиеся должны уяснить, что потенциальная энергия не появляется сама по себе. В этих опытах гиря была поднята над столом, пружина была сжата какой–то силой. Значит, чтобы тело запасло потенциальную энергию, необходимосовершить работу. Чем сильнее будет сжата пружина, чем выше будет поднято тело, тем больше у них будет запас потенциальной энергии. Потенциальная энергия – это энергия, обусловленная взаимным расположением взаимодействующих тел или частей тела.
Количественные расчеты выполняют только для потенциальной энергии тела, поднятого над поверхностью Земли (рисунок 4.4).

Рисунок 4.4
 · (4.9)
· (4.9)
Потенциальная энергия является относительной величиной.Поэтому, приводя значение потенциальной энергии, необходимо указывать уровень, относительно которого она задана, – нулевой уровень потенциальнойэнергии (поверхность пола, потолка и т. д.).
Формулу для потенциальной энергии деформированной пружины не вводят, а ее существование обосновывают на качественном уровне с опорой на эксперимент.
Важно показать учащимся, что потенциальная энергия может проявиться лишь при определенных условиях: например, поднятая гиря или закрученная пружина только тогда приведут в движение часовой механизм, когда гире будет предоставлена возможность падать, а пружине − раскручиваться. Если неподвижные тела могут совершать механическую работу, значит, обладают потенциальной энергией. Значение потенциальной энергии зависит от взаимного расположения взаимодействующих тел и изменяется только при совершении работы.
Подвести итоги изучения двух видов энергии, можно, используя таблицу 4.2.
Таблица 4.2
Сходства и различия кинетической и потенциальной энергий
| Кинетическая энергия | Потенциальная энергия | |
| Сходства | 1.Физическая величина, характеризующая способность тела (или нескольких тел) совершать работу. | |
| 2.Мерой изменения энергии при переходе из одного состояния в другое является работа. | ||
| 3.Основной единицей в СИ является 1 Дж (джоуль). | ||
| 4.Числовые значения кинетической и потенциальной энергии относительны. | ||
| Различия | 1.Энергия, которой обладает тело вследствие своего движения. | 1.Энергия взаимодействия тел или частей тела. |
2. 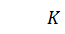 . .
| 2.В поле силы тяжести
 . .
| |
| 3.Численно равна работе, которую должна совершить сила, действующая не тело, чтобы разогнать его из состояния покоя до заданной скорости. | 3.Зависит от силы взаимодействия тел (или частей тела) и расстояния между ними. Для деформированного тела потенциальная энергия зависит от величины деформации и упругих свойств тела. |
Закон сохранения механической энергии
Взаимные превращения механической энергии из одного вида в другой удобно иллюстрировать опытами по падению тела, движению тела, брошенного вертикально, (движению тела по наклонной плоскости) вверх и вниз. Эти опыты просты, но требуют тщательного логического объяснения.
Проанализируем движение брошенного вверх металлического шарика (рисунок 4.5).
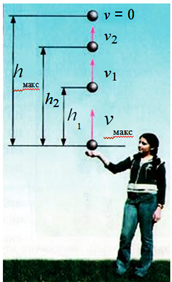
Рисунок 4.5
В нижней точке траектории сила действия руки на шарик сообщает ему кинетическую энергию. Шарик движется вверх. Скорость его движения, а значит, и кинетическая энергия уменьшаются. Но исчезает ли кинетическая энергия бесследно? Поднимаясь все выше, шарик приобретает все большую потенциальную энергию. В верхней точке подъема кинетическая энергия шарика равна нулю, а потенциальная – максимальна. Значит, в рассмотренном примере происходит превращение энергии из одного вида (кинетической) в другой (потенциальную). При возвращении шарика обратно снова будет идти превращение энергии: с уменьшением высоты (и потенциальной энергии) увеличивается скорость движения шарика (и кинетическая энергия).
Если сопротивление воздуха мало (и им можно пренебречь), брошенный вверх шарик возвращается назад практически с такой же, как в момент бросания, скоростью и кинетической энергией.
А каким будет значение механической энергии шарика в промежуточных точках? Например, на высоте h 1. При подъеме шарика на высоту h 1 его кинетическая энергия уменьшилась, но при этом появилась потенциальная энергия.
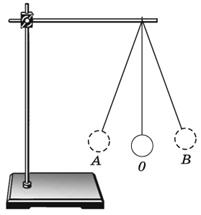 |  | ||
Демонстрируя опыты, следует в процессе обсуждения с учащимися выяснить следующие вопросы. Какой энергией и почему обладает тело, когда оно находится в верхнем положении? На каком основании можно утверждать, что эта энергия уменьшается? Как при подъеме (падении) меняются скорость тела и его кинетическая энергия? Все ответы учащиеся должны обосновать. Это же следует сделать при демонстрации других опытов, таких как нитяной маятник (рисунок 4.6, а) и маятник Максвелла (рисунок 4.6, б), сопровождая эти демонстрации соответствующими пояснениями.
а б
Рисунок 4.6
После чего учащиеся приходят к вводу, что полная механическая энергия тела (системы тел),равная сумме кинетической и потенциальной энергий (Е = K+П), сохраняется. Данное утверждение о постоянстве механической энергии в физике называют законом сохранения механической энергии.
Для закрепления закона сохранения механической энергии и более наглядного представления превращения одного вида энергии в другой, целесообразно использование соответствующей компьютерной модели из ЭСО «Наглядная физика. Введение» (рисунок 4.7).
Здесь наглядно можно проследить за изменением в процентном соотношении кинетической и потенциальной энергии и убедится, что полная механическая энергия тела, равная сумме кинетической и потенциальной энергий, сохраняется.

Рисунок 4.7
С целью обобщения и систематизации знаний о превращениях энергии при движении тела, брошенного вертикально вверх, или вверх по наклонной плоскости, начиная с момента бросания до момента возврата в начальную точку целесообразно вместе с учащимися заполнить таблицу 4.3.
Таблица 4.3
Сохранение и превращение энергии
| № п/п | Движение тела в поле тяготения | |||
| Вверх | Вниз | |||
| Состояние | Энергия | Состояние | Энергия | |
Начальное
υ 0 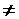 0, h 0, h  = 0 = 0
|  , П=0, , П=0,

| Начальное
υ 0= 0, h  = Н = Н
| К = 0, П = gmН, Е = К + П = gmН | |
Промежуточное
υ 1, h 
|  ,
П ,
П  = gmh = gmh  , ,

| Промежуточное υ 1, h 1 |  ,
П ,
П  = =gmh = =gmh  , ,

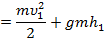
| |
Конечное
Υ 2= 0, h  = Н = Н
| К  = 0, П = 0, П  = gmН,
Е = К+П = gmН = gmН,
Е = К+П = gmН
| Конечное
υ 2, h  = 0 = 0
|  , П , П  =0, =0,
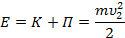
|