Рассмотрим следующий вариант построения алгоритмов управления. Он связан с разработкой алгоритмов оценивания параметров движения ведущего ЛА по результатам измерений относительного движения. Поскольку измерения содержат случайные ошибки, а алгоритм оценки должен быть эффективным в смысле их снижения и снижения влияния этих ошибок на точность получаемых оценок параметров движения ведущего ЛА, то есть алгоритм обработки информации должен обеспечивать фильтрацию ошибок измерений и идентификацию параметров движения ведущего ЛА.
В общем случае алгоритм оценки и идентификации включает в себя блоки первичной и вторичной обработки измерительной информации. Ввиду того, что блок первичной обработки является составной частью измерительной системы и конструктивно с ней совмещен, то алгоритм первичной обработки информации здесь не рассматривается. Основное внимание при дальнейших исследованиях уделяется методам вторичной обработки информации по результатам первичных измерений.
Сначала рассмотрим общие вопросы идентификации моделей динамических систем. Задачу идентификации [5] или, другими словами, задачу оценивания параметров динамической системы можно сформулировать как задачу оценивания параметров модели системы, которая обладает существенными чертами проектируемой системы и представляет знания об этой системе в удобной форме. То есть целью идентификации не является абсолютно точное математическое описание физической реальности, а лишь создание модели, отражающей существенные для дальнейшего применения свойства системы. Положение существенно усложняется, если дополнительно с вектором параметров необходимо оценивать и вектор состояния. Здесь следует обратить внимание на то, что идентификация параметров даже для линейных систем приводит к нелинейным методам оценивания и идентификации.
В настоящее время опубликовано значительное число работ математического характера по оптимальной нелинейной фильтрации. Наиболее общее решение проблемы нелинейной фильтрации получено Р.Л.Стратоновичем в его работах по теории условных марковских процессов [6]. Как показано в работе [6], получение оптимальной нелинейной оценки сводится к решению функционального рекуррентного соотношения для апостериорной плотности вероятности. Основной особенностью задач нелинейной фильтрации является то, что реализация оптимальных алгоритмов обработки информации на современном уровне развития вычислительной техники не представляется возможной из-за сложности решения уравнений для апостериорной плотности вероятности, включающим многомерное интегрирование. Этот факт обусловил появление большого числа работ, посвященных разработке субоптимальных алгоритмов нелинейной фильтрации, основанных на различных аппроксимациях апостериорной плотности вероятности. Разработка субоптимальных алгоритмов диктуется также необходимостью реализации их в системах, работающих в реальном времени и удобством реализации на ЦВМ. С этой точки зрения предпочтительны рекуррентные методы, требующие запоминания на каждом такте сравнительно небольшого числа результатов вычислений.
Рассмотрим теперь конкретно задачу построения алгоритмов CMCН ДПЛА с идентификатором в контуре управления. Имеется несколько вариантов синтеза. В этом случае задача сводится к отысканию расчетных соотношений для параметров  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  в предположении, что имеется информация о параметрах относительного движения
в предположении, что имеется информация о параметрах относительного движения  ,
,  ,
,  ,
,  ,
,  ,
,  , измеренных с помехами, и параметрах полета ведомого ЛА. Указанные параметры необходимы для реализации алгоритмов СМСН.
, измеренных с помехами, и параметрах полета ведомого ЛА. Указанные параметры необходимы для реализации алгоритмов СМСН.
Рассмотрим относительное движение двух ЛА в пространстве. В этом случае изменение углов места и азимута, дальности, угловых скоростей линии визирования, радиальной скорости описывается в основной СК системой уравнений вида:

| (13) |

| |

| |

| |

| |
 , ,
|
где  ,
,  ,
,  .
.
Эта система может быть положена в основу синтеза алгоритмов нелинейной фильтрации для получения оценок  ,
,  ,
,  , идентификации
, идентификации  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Для вычисления оценок параметров  ,
,  ,
,  ,
,  ,
,  ,
, 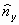 , и т.д. необходимо определить математические ожидания этих функций на основе плотности распределения оценок
, и т.д. необходимо определить математические ожидания этих функций на основе плотности распределения оценок  ,
,  ,
,  ,
,  ,
,  ,
,  . Поскольку этот путь связан с громоздкими вычислениями многомерных интегралов, можно использовать более простой, но приближенный способ, согласно которому оценки перечисленных параметров вычисляются по определенным формулам, куда в качестве
. Поскольку этот путь связан с громоздкими вычислениями многомерных интегралов, можно использовать более простой, но приближенный способ, согласно которому оценки перечисленных параметров вычисляются по определенным формулам, куда в качестве  ,
,  ,
,  ,
,  ,
,  ,
,  входят их оценки. Используя информацию об этих оценках, можно определить значения относительных скоростей и ускорений в траекторной СК ведущего ЛА, сформировать программные значения.
входят их оценки. Используя информацию об этих оценках, можно определить значения относительных скоростей и ускорений в траекторной СК ведущего ЛА, сформировать программные значения.
Таким образом, основная задача состоит в определении оценок  ,
,  ,
,  ,
,  ,
,  ,
,  . Конкретному рассмотрению алгоритмов оценивания и идентификации параметров относительного движения ЛА предпошлем краткое изложение некоторых общих принципов их построения.
. Конкретному рассмотрению алгоритмов оценивания и идентификации параметров относительного движения ЛА предпошлем краткое изложение некоторых общих принципов их построения.
Методически исследование по выбору алгоритмов обработки информации в СМСН ДПЛА проводилось по следующей схеме Это, в первую очередь, касалось замены исходной нелинейной модели состояния и наблюдений тем или иным приближением и построение алгоритма оценивания на основе такой аппроксимации. Во-первых, для решения поставленной проблемы используется подход, основанный на дискретной аппроксимации динамической модели относительного движения. Это позволяет наиболее эффективно реализовать алгоритмы нелинейной фильтрации в БЦВМ, в основу которых положены дискретные методы оценивания. Во-вторых, нелинейные уравнения модели и наблюдений раскладываются в ряд Тейлора до членов первого порядка включительно относительно оценки на предыдущем шаге. В-третьих, в качестве математических моделей идентифицируемых параметров системы используются локальные модели, описывающие изменения параметров лишь в узком диапазоне изменения времени. Простейшей локальной моделью изменения параметров является следующая:
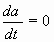 , ,
| (14) |
где  вектор параметров,
вектор параметров,  время.
время.
Другая локальная модель изменения параметров может быть представлена в виде:
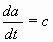 , ,
| (15) |
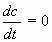 , ,
|
где вектор  подлежит оценке наряду с вектором
подлежит оценке наряду с вектором  . В дискретном виде эти модели можно записать соответственно как
. В дискретном виде эти модели можно записать соответственно как
 , ,
| (16) |
и
 , ,
| (17) |
 . .
|
В принципе, значение степени полинома можно повысить, но это усложнение приводит лишь к незначительному увеличению точности оценки.
В введении таких моделей состоит способ расширения вектора состояния, позволяющий получить принципиальное решение задачи совместной идентификации параметров и оценивания вектора состояния. Включая в число компонент расширенного вектора состояния 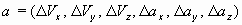 параметры вектора локальной модели (16), получим уравнения динамической системы двенадцатого порядка.
параметры вектора локальной модели (16), получим уравнения динамической системы двенадцатого порядка.
Однако здесь возникает ряд проблем вычислительного порядка, связанных с увеличением размерности задачи оценивания, что ведет к значительному увеличению объема вычислений, и как следствие - к неустойчивости машинных алгоритмов.
В таких условиях чрезвычайно важное, если не решающее, значение приобретает исследование возможностей сведения исходной задачи совместной идентификации, имеющей большую размерность, к задачам меньшей размерности, т.е. возможностей декомпозиции задачи оценивания расширенного вектора состояния (сведение ее к задачам меньшей размерности).
Поэтому в данной работе в качестве одного из путей построения алгоритма оценивания в СМСН ДПЛА предлагается сначала провести идентификацию параметров  ,
,  ,
,  и оценить параметры
и оценить параметры  ,
,  ,
,  , a затем, уже с учетом этой информации, осуществить идентификацию параметров
, a затем, уже с учетом этой информации, осуществить идентификацию параметров  ,
,  ,
,  . В свете этих предложений идентификацию параметров целесообразно осуществлять в два этапа. Таким образом, идея этого метода интересна, так как позволяет существенно упростить алгоритмы обработки информации СМСН ДПЛА. Следуя намеченной схеме, решение задачи нелинейной фильтрации при поиске оценок параметров относительного движения ЛА ищется с помощью модифицированного нелинейного фильтра.
. В свете этих предложений идентификацию параметров целесообразно осуществлять в два этапа. Таким образом, идея этого метода интересна, так как позволяет существенно упростить алгоритмы обработки информации СМСН ДПЛА. Следуя намеченной схеме, решение задачи нелинейной фильтрации при поиске оценок параметров относительного движения ЛА ищется с помощью модифицированного нелинейного фильтра.
При решении практических задач идентификации возникает проблема обеспечения устойчивости процессов обработки информации. В некоторых случаях реальные ошибки оценивания могут во много раз превосходить расчетные значения, характеризуемые матрицей ковариации ошибок оценивания. Наиболее часто встречающимся источником расходимости являются неточности моделей состояния и наблюдения, неточность задания характеристик шумов и т.д. Так как синтез алгоритмов обычно проводится в условиях априорной неопределенности, то для ее преодоления используют различные адаптивные алгоритмы.
В данной работе с целью устранения в определенных пределах незнания о характеристиках шумов измерений используется идея J-адаптивного фильтра. Такое название он получил по первой букве фамилии автора “J” предложивший алгоритм J-адаптивного фильтра для дискретных систем в работе [7].
В работе [7] J-адаптивный фильтр использован для оценивания параметров движения баллистического объекта: положения и скорости, а также для оценивания вектора аэродинамических параметров (коэффициентов лобового сопротивления и подъемной силы) или составляющих вектора немоделируемых ускорений по осям декартовой СК. Как указано в этой работе, J-адаптивный фильтр идентифицирует 99% немоделируемых ускорений.
Пусть динамика системы описывается следующим нелинейным уравнением:

| (18) |
В дискретной форме это уравнение (с точностью до членов второго порядка) будет иметь вид [7]:
 , ,
| (19) |
где  вектор состояния размерности
вектор состояния размерности  ,
,  непрерывная векторная функция, которая по крайней мере дважды дифференцируема по своим аргументам,
непрерывная векторная функция, которая по крайней мере дважды дифференцируема по своим аргументам,
 , ,
| (20) |
матрица Якоби вектор-функции  , a
, a  отражает погрешность дискретизации и неопределенности моделирования в уравнении динамики. Предполагается, что
отражает погрешность дискретизации и неопределенности моделирования в уравнении динамики. Предполагается, что  является белой гауссовской последовательностью с нулевым средним и матрицей ковариации
является белой гауссовской последовательностью с нулевым средним и матрицей ковариации  :
:
 , ,
| (21) |
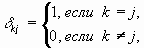
|
где  дельта-функция Кронекера.
дельта-функция Кронекера.
Начальное значение вектора состояния  принимается гауссовской случайной переменной с известными средним значением и матрицей ковариации вида:
принимается гауссовской случайной переменной с известными средним значением и матрицей ковариации вида:

| (22) |
Процесс измерения описывается уравнением:
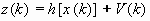 , ,
| (23) |
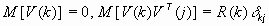 , ,
|
где  вектор погрешностей измерений типа белой последовательности с нулевым средним и матрицей ковариации
вектор погрешностей измерений типа белой последовательности с нулевым средним и матрицей ковариации 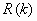 ,
,  вектор размерности
вектор размерности  ,
,  непрерывная векторная функция, дважды дифференцируемая по своим аргументам.
непрерывная векторная функция, дважды дифференцируемая по своим аргументам.
Тогда обобщенный калмановский фильтр описывается следующими уравнениями:
 , ,
| (24) |
 , ,
| (25) |
где 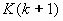 весовая матрица (матрица коэффициентов усиления фильтра).
весовая матрица (матрица коэффициентов усиления фильтра).
Уравнения экстраполяции матрицы ковариации:
 , ,
| (26) |
 . .
|
Уравнения коррекции матрицы ковариации:
 , ,
| (27) |
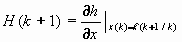 . .
|
Далее на основе [8] рассмотрим метод получения J-адаптивного нелинейного фильтра.
Предполагается, что в уравнения состояния и измерений входят одни и те же определенные параметры, величины которых известны неточно. Такие параметры можно представить как случайные переменные с заранее известной статистикой 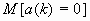 ,
,  При этом предполагается, что
При этом предполагается, что  ,
,  ,
,  ,
,  некоррелированы, и матрица ковариации
некоррелированы, и матрица ковариации  остается неизменной на всем временном интервале процесса оценивания.
остается неизменной на всем временном интервале процесса оценивания.
При синтезе фильтра в вектор состояния  включается вектор
включается вектор  . Вводя для вектора параметров уравнения вида
. Вводя для вектора параметров уравнения вида
 , ,
| (28) |
можно получить расширенную систему уравнений с вектором состояния:
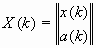 , ,
| (29) |
и уравнениями измерений:
 . .
| (30) |
В этом случае динамические уравнения расширенной системы запишутся в виде
 , ,
| (31) |
 . .
|
Применяя к этой системе нелинейный фильтр можно получить оценки как вектора  , так и вектора
, так и вектора  .
.
Далее, используя метод изложенный в работе [9], легко получить уравнения J-адаптивного фильтра. Уравнения J-адаптивного фильтра получаются [9] с помощью расширения вектора состояния  путем присоединения переменной
путем присоединения переменной  , записи расширенного фильтра в виде отдельных уравнений и отбрасывания уравнений для ковариационной матрицы
, записи расширенного фильтра в виде отдельных уравнений и отбрасывания уравнений для ковариационной матрицы  .
.
В соответствии с этим методом матрица ковариации ошибок оценивания представляется в виде:
 , ,
| (32) |
где
 , ,
| (33) |
 . .
|
Матрицу  можно представить в виде
можно представить в виде
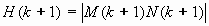 ,
где ,
где
| (34) |
 , ,  , ,
|
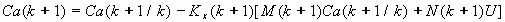 , ,
| (35) |

|
где
 , ,
| (36) |
 , ,
| |

|
Окончательный вид уравнений J-адаптивного фильтра будет следующий:
 , ,
| (37) |
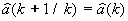 , ,
| |

| |
 , ,
| |
 , ,
| |
 , ,
| |
 . .
|
Заключение
В данной работе решена задача оценки параметров относительного движения ЛА в групповом полете. Точное определение параметров  ,
,  ,
,  , и особенно
, и особенно  ,
,  ,
,  , необходимо для синтеза алгоритма управления полетом ЛА в группе.
, необходимо для синтеза алгоритма управления полетом ЛА в группе.
Задача была рассмотрена при полном составе измерений параметров относительного движения ЛА: углах визирования, угловой скорости линии визирования, дальности и скорости изменения дальности.
Ключевым вопросом в решении этой задачи стала разработка математической модели относительного движения ЛА.
Ввиду того, что измерения содержат случайные ошибки. алгоритм оценивания должен обеспечивать снижение ошибок и снижение их влияние точность оценки, а следовательно и на качество управления строем БЛА. Следовательно, в алгоритме было необходимо провести фильтрацию ошибок измерений.
Эта задача была решена посредством применения J-адаптивного фильтра.
Список литературы
Терентьев В.М. Разработка и исследование алгоритмов управления и обработки информации для СМСН БЛА. Доклад на школе-семинаре ЦАГИ по проблемам управления ЛА г. Жуковский 25.02-2.03 1991 г.
Тарасов В.Г. Межсамолетная навигация. М.: Машиностроение, 1980. 184 с.
Степанов О.А. Применение теории нелинейной фильтрации в задачах обработки навигационной информации. М. ЦНИИ "Электроприбор", 2000.
Горбатенко С.А., Макашов Э.М. и др. Механика полетов. Инженерный справочник. М.: Машиностроение, 1969, 420 с.
Эйкхоф П. Основы идентификации систем управления. М.: Мир, 1975.
Стратонович Р.Л. Условные марковские процессы и их применение к теории оптимального управления. М.: Издательство МГУ, 1966.
Вопросы управления космическими аппаратами. М.:Мир, 1975.
Jazwinski A.H., Stochastic processes and filtering theory, NY.: Academic Press, 1970.
Jazwinski A.H. Nonlinear and adaptive estimation in reentry, AIAA Paper No. 72-874.
Для подготовки данной работы были использованы материалы с сайта https://www.sciteclibrary.ru