_____________________________________________________________________________


 «Я должен еще подумать!» Очистить геометрию Евклида от «пятна», доказать знаменитый его пятый постулат пытались на протяжении 20 веков многие ученые. Вот далеко не полный список этих попыток: Птолемей (II в.), Прокл (IVв.), Ибн Аль Хайсам (Хв.), Омар Хайям (ХI в.), Насир ад-Дин ат-Туси (ХIIIв.), Клавий (1514); Катальди (1603), Борелли (1658), Витале (1680), Валлис (1663), Саккери (1733), Ламберт (1766), Бертран (1778), Лагранж (1810), Лежандр (1823).
«Я должен еще подумать!» Очистить геометрию Евклида от «пятна», доказать знаменитый его пятый постулат пытались на протяжении 20 веков многие ученые. Вот далеко не полный список этих попыток: Птолемей (II в.), Прокл (IVв.), Ибн Аль Хайсам (Хв.), Омар Хайям (ХI в.), Насир ад-Дин ат-Туси (ХIIIв.), Клавий (1514); Катальди (1603), Борелли (1658), Витале (1680), Валлис (1663), Саккери (1733), Ламберт (1766), Бертран (1778), Лагранж (1810), Лежандр (1823).
 Известен курьезный случай, когда Жозеф Луи Лагранж, делая доклад в парижской академии наук со своим доказательством аксиомы параллельных, вдруг оборвал его со словами: «Я должен об этом еще подумать!» К началу ХIХ века количество ошибочных доказательств аксиомы параллельных достигло 55. Николай Лобачевский сказал об этом так: «Напрасные старания в продолжение двух тысяч лет».
Известен курьезный случай, когда Жозеф Луи Лагранж, делая доклад в парижской академии наук со своим доказательством аксиомы параллельных, вдруг оборвал его со словами: «Я должен об этом еще подумать!» К началу ХIХ века количество ошибочных доказательств аксиомы параллельных достигло 55. Николай Лобачевский сказал об этом так: «Напрасные старания в продолжение двух тысяч лет».
Как правило, ошибки всех подобных «доказательств» состояли в том, что их авторы брали на веру какое-нибудь другое очевидное утверждение, из которого они уже строго выводили потом знаменитый пятый постулат Евклида. По сути эти допущения были другими формами того же постулата, то есть все они были эквивалентны ему. Давайте приведем здесь некоторые из них:

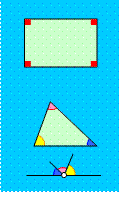 Эквиваленты аксиомы параллельных:
Эквиваленты аксиомы параллельных:
1) Параллельность различных прямых передается по транзиту;
2) Существует хотя бы один прямоугольник;
3) Сумма углов во всех треугольниках одинакова;
4) Сумма углов хотя бы в одном треугольнике равна 1800;
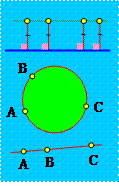
5) Все точки с одной стороны от прямой линии, лежащие на
одинаковом расстоянии от нее, находятся на одной прямой;
6) Через любые три точки проходит либо прямая,
либо окружность;
7) Существуют неравные треугольники с тремя одинаковыми
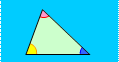 углами;
углами;
8)  Любая прямая, проходящая через точку внутри острого угла, пересекает хотя бы одну его сторону.
Любая прямая, проходящая через точку внутри острого угла, пересекает хотя бы одну его сторону.
Если принять на веру любое из этих утверждений, мы сразу окажемся в «плоской» геометрии Евклида, то есть на бесконечном ровном листе бумаги, где нет никакой «кривизны». Если отвергнуть любое из этих утверждений – то геометрия сразу станет искривленной, неплоской, гораздо более сложной. Такую геометрию обычно называют неевклидовой или геометрией Лобачевского.
Геометрия Лобачевского. Что же будет, если отвергнуть Пятый постулат Евклида? Очевидно, что тогда через данную точку на плоскости можно будет провести больше одной прямой, параллельной данной. Больше одной — значит, как минимум, две. Именно так и сформулировал великий русский математик Николай Иванович Лобачевский 11 февраля 1826 года главный постулат своей геометрии.
| АКСИОМА ЛОБАЧЕВСКОГО: Через одну точку, не лежащую на прямой, в заданной ими плоскости можно провести больше одной прямой, параллельной данной прямой. | 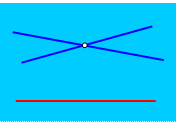
|

 Сразу бросается в глаза, что аксиома Лобачевского является прямым отрицанием аксиомы параллельных Евклида. И это не случайно: Николай Лобачевский, как и многие его предшественники, сначала тоже пытался доказать Пятый постулат Евклида. Он даже привел свое доказательство на лекции перед студентами, но после тоже нашел в нем ошибку. Неудивительно, что Лобачевский начал доказывать аксиому параллельных методом «от противоположного». Удивительно то, что получив на этом пути множество очень странных выводов, он не остановился в своем исследовании, а продолжал его дальше. Ведь полученные им результаты противоречили всякому здравому смыслу! Например, в его новой геометрии получалось, что существует прямая, которая проходит через точку внутри острого угла и не пересекает его сторон. Попробуйте такое себе представить! Все точки, которые в одной полуплоскости находятся на равных расстояниях от данной прямой, там образовывали кривую линию. Если вдуматься, в этом нет ничего странного — ведь в геометрии Лобачевского не действует Пятый постулат Евклида. Но современникам Николая Лобачевского это было трудно понять, над ним просто смеялись. Не помогло даже то, что Лобачевский был ректором Казанского университета — то есть очень уважаемым человеком. Ведь сама природа, казалось, противоречила его выводам: легко ли себе представить, что существует геометрия, где нет ни одного квадрата, даже нет ни одного прямоугольника! Посмотрите вокруг — нас с вами окружают одни квадраты и прямоугольники: плитки на полу, столы и двери, скамейки и тетради... Тем не менее, в новой геометрии Николай Лобачевский не мог обнаружить противоречия. Да его там и не было, но поняли это уже только после его смерти. Оказалось, что подобная геометрия существует на кривых поверхностях, точнее — на поверхностях, кривизна которых отрицательна. Такие поверхности устроены довольно сложно, а вот поверхность с положительной кривизной нам должна быть очень хорошо знакома. Это поверхность нашего с вами Земного Шара. На ней тоже нет ни одного квадрата и ни одного прямоугольника, и при этом на ней нет никаких противоречий!
Сразу бросается в глаза, что аксиома Лобачевского является прямым отрицанием аксиомы параллельных Евклида. И это не случайно: Николай Лобачевский, как и многие его предшественники, сначала тоже пытался доказать Пятый постулат Евклида. Он даже привел свое доказательство на лекции перед студентами, но после тоже нашел в нем ошибку. Неудивительно, что Лобачевский начал доказывать аксиому параллельных методом «от противоположного». Удивительно то, что получив на этом пути множество очень странных выводов, он не остановился в своем исследовании, а продолжал его дальше. Ведь полученные им результаты противоречили всякому здравому смыслу! Например, в его новой геометрии получалось, что существует прямая, которая проходит через точку внутри острого угла и не пересекает его сторон. Попробуйте такое себе представить! Все точки, которые в одной полуплоскости находятся на равных расстояниях от данной прямой, там образовывали кривую линию. Если вдуматься, в этом нет ничего странного — ведь в геометрии Лобачевского не действует Пятый постулат Евклида. Но современникам Николая Лобачевского это было трудно понять, над ним просто смеялись. Не помогло даже то, что Лобачевский был ректором Казанского университета — то есть очень уважаемым человеком. Ведь сама природа, казалось, противоречила его выводам: легко ли себе представить, что существует геометрия, где нет ни одного квадрата, даже нет ни одного прямоугольника! Посмотрите вокруг — нас с вами окружают одни квадраты и прямоугольники: плитки на полу, столы и двери, скамейки и тетради... Тем не менее, в новой геометрии Николай Лобачевский не мог обнаружить противоречия. Да его там и не было, но поняли это уже только после его смерти. Оказалось, что подобная геометрия существует на кривых поверхностях, точнее — на поверхностях, кривизна которых отрицательна. Такие поверхности устроены довольно сложно, а вот поверхность с положительной кривизной нам должна быть очень хорошо знакома. Это поверхность нашего с вами Земного Шара. На ней тоже нет ни одного квадрата и ни одного прямоугольника, и при этом на ней нет никаких противоречий!
Николай Иванович Лобачевский провел 40 лет в Казанском университете, из которых 19 лет был его ректором. Его усилиями этот университет стал одним из лучших в России. Он читал лекции по арифметике, теории вероятностей, алгебре и геометрии, по физике, астрономии и даже гидравлике. Писал учебники для гимназий и заведовал библиотекой. Также его интересовали химия, ботаника и анатомия человека. Известно, что в юности после смерти своего старшего брата, он два года посвятил медицине. Более 30 лет своей жизни Николай Лобачевский в одиночку создавал совершенно новую неевклидову  геометрию. Эти занятия «дорого ему стоили» — научное общество Петербурга резко критиковало эти его труды. Чего стоит, например, отзыв о его работе академика Остроградского: «Автор, по-видимому, задался целью писать таким образом, чтобы его нельзя было понять. Он достиг этой цели; большая часть книги осталась для меня столь же неизвестной, как если бы я никогда не видал её... Все, что я понял в геометрии Лобачевского – ниже посредственного. Из этого я вывел заключение, что книга господина ректора Лобачевского опорочена ошибками, что она небрежно изложена и, следовательно, не заслуживает внимания Академии.» Лобачевскому не дали защитить диссертацию, и его авторитет как ученого сильно пошатнулся. Вот какова была цена человеческого непонимания!
геометрию. Эти занятия «дорого ему стоили» — научное общество Петербурга резко критиковало эти его труды. Чего стоит, например, отзыв о его работе академика Остроградского: «Автор, по-видимому, задался целью писать таким образом, чтобы его нельзя было понять. Он достиг этой цели; большая часть книги осталась для меня столь же неизвестной, как если бы я никогда не видал её... Все, что я понял в геометрии Лобачевского – ниже посредственного. Из этого я вывел заключение, что книга господина ректора Лобачевского опорочена ошибками, что она небрежно изложена и, следовательно, не заслуживает внимания Академии.» Лобачевскому не дали защитить диссертацию, и его авторитет как ученого сильно пошатнулся. Вот какова была цена человеческого непонимания!



 Ради справедливости, необходимо сказать, что не все современники Николая Ивановича Лобачевского не могли его понять. В это же время в Германии жил и работал знаменитый математик Карл Гаусс, который получил множество глубоких результатов в арифметике и алгебре, а будучи еще юношей, смог построить циркулем и линейкой правильный 17 угольник. Гаусса даже называли «королем» математиков, хотя его отец был простой садовник. Гаусс тоже много думал над проблемой Пятого постулата Евклида и одно время даже занимался геометрией кривых поверхностей. Видимо, он был первым, кто догадался о существовании других геометрий. Известно, что Гаусс измерял углы треугольника, образованного тремя горными пиками и надеялся обнаружить отличие в своих измерениях от теории Евклида. Однако он публично хранил молчание об этих исследованиях и не опубликовал своих результатов — видимо, боялся уронить этим свой авторитет в научном мире. В 1819 году Гаусс получает письмо некого Фердинанда Швейкарта, в котором тот пишет, что обнаружил «звездную» геометрию, где нет необходимости в Пятом постулате Евклида. В том же письме Швейкарт сообщал, что обычная геометрия является лишь ограниченной частью «звездной», в которой сумма углов любого треугольника меньше двух прямых углов. Ответ Гаусса на это письмо был таким: «Почти все это списано с моей души!». Сам Фердинанд Швейкарт был профессором римского права и математикой занимался как любитель. Он тоже не опубликовал своих исследований, хотя наверняка сделал бы это первым. До конца своей жизни Гаусс публично хранил молчание о геометрии без аксиомы параллельных, но даже в своих мыслях он продвинулся в ней не так далеко, как Лобачевский. Когда в 1840 году Николай Лобачевский впервые опубликовал свои результаты на немецком языке, в научной среде Германии их тоже не поняли. Однако Карл Гаусс прочел эту книгу и был восхищен ею, о чем написал своим друзьям. После смерти в его библиотеке были найдены два экземпляра «Геометрических исследований» Лобачевского. Более того, в 1842 году Гаусс предложил избрать никому тогда неизвестного Лобачевского в академики Геттингенского ученого общества и послал ему об этом письмо и соответствующий диплом. Вот его рекомендация: «Королевскому обществу позволю себе предложить в корреспонденты нашего общества русского имперского статского советника Н. Лобачевского, профессора в Казани, одного из самых выдающихся математиков русского государства». Гаусс даже стал учить русский язык, чтобы прочитать другие труды Лобачевского в оригинале! Вот выдержка из его письма: «Я начинаю читать по-русски довольно успешно и нахожу в этом большое удовольствие. Господин Кнорре прислал мне небольшой мемуар Лобачевского, написанный им по-русски, и как этот мемуар, так и небольшая книжка о параллельных линиях на немецком языке… возбудили во мне желание узнать больше об этом остроумном математике». Правда, даже Гаусс сообщает о трудности понимания работ Лобачевского: «Его работы можно уподобить запутанному лесу, через который нельзя найти дороги, не изучив предварительно каждого дерева».
Ради справедливости, необходимо сказать, что не все современники Николая Ивановича Лобачевского не могли его понять. В это же время в Германии жил и работал знаменитый математик Карл Гаусс, который получил множество глубоких результатов в арифметике и алгебре, а будучи еще юношей, смог построить циркулем и линейкой правильный 17 угольник. Гаусса даже называли «королем» математиков, хотя его отец был простой садовник. Гаусс тоже много думал над проблемой Пятого постулата Евклида и одно время даже занимался геометрией кривых поверхностей. Видимо, он был первым, кто догадался о существовании других геометрий. Известно, что Гаусс измерял углы треугольника, образованного тремя горными пиками и надеялся обнаружить отличие в своих измерениях от теории Евклида. Однако он публично хранил молчание об этих исследованиях и не опубликовал своих результатов — видимо, боялся уронить этим свой авторитет в научном мире. В 1819 году Гаусс получает письмо некого Фердинанда Швейкарта, в котором тот пишет, что обнаружил «звездную» геометрию, где нет необходимости в Пятом постулате Евклида. В том же письме Швейкарт сообщал, что обычная геометрия является лишь ограниченной частью «звездной», в которой сумма углов любого треугольника меньше двух прямых углов. Ответ Гаусса на это письмо был таким: «Почти все это списано с моей души!». Сам Фердинанд Швейкарт был профессором римского права и математикой занимался как любитель. Он тоже не опубликовал своих исследований, хотя наверняка сделал бы это первым. До конца своей жизни Гаусс публично хранил молчание о геометрии без аксиомы параллельных, но даже в своих мыслях он продвинулся в ней не так далеко, как Лобачевский. Когда в 1840 году Николай Лобачевский впервые опубликовал свои результаты на немецком языке, в научной среде Германии их тоже не поняли. Однако Карл Гаусс прочел эту книгу и был восхищен ею, о чем написал своим друзьям. После смерти в его библиотеке были найдены два экземпляра «Геометрических исследований» Лобачевского. Более того, в 1842 году Гаусс предложил избрать никому тогда неизвестного Лобачевского в академики Геттингенского ученого общества и послал ему об этом письмо и соответствующий диплом. Вот его рекомендация: «Королевскому обществу позволю себе предложить в корреспонденты нашего общества русского имперского статского советника Н. Лобачевского, профессора в Казани, одного из самых выдающихся математиков русского государства». Гаусс даже стал учить русский язык, чтобы прочитать другие труды Лобачевского в оригинале! Вот выдержка из его письма: «Я начинаю читать по-русски довольно успешно и нахожу в этом большое удовольствие. Господин Кнорре прислал мне небольшой мемуар Лобачевского, написанный им по-русски, и как этот мемуар, так и небольшая книжка о параллельных линиях на немецком языке… возбудили во мне желание узнать больше об этом остроумном математике». Правда, даже Гаусс сообщает о трудности понимания работ Лобачевского: «Его работы можно уподобить запутанному лесу, через который нельзя найти дороги, не изучив предварительно каждого дерева».

 Есть еще один человек, имя которого навсегда связанно с открытием новой неевклидовой геометрии. Его зовут Янош Больяй. Он был венгром, а Венгрия тогда принадлежала Австрийской империи. Еще в детстве Янош проявил способности к математике и музыке: к 10 годам он имел собственные музыкальные сочинения, а в 13 лет овладел уже основами дифференциального и интегрального исчислений. Его отец, Фракаш Больяй, сам был математиком и даже другом знаменитого Гаусса. Отец хотел, чтобы его сын учился у его великого друга, но вышло по-другому. В 20 лет Янош заканчивает военно-инженерную академию в Вене и тогда же увлекается теорией параллельных. Об этом он сообщает своему отцу и получает от него следующий красноречивый ответ: «Ты не должен пытаться одолеть теорию параллельных линий... я знаю этот путь, я прошел его до конца, я пережил эту беспросветную ночь, и всякий светоч, всякую радость жизни я похоронил в ней... Молю тебя: оставь в покое учение о параллельных — оно лишит тебя здоровья, досуга и покоя, оно погубит для тебя всю радость жизни». Согласитесь, после такого высокопарного предостережения трудно было сыну удержаться не заглянуть в эту «бездну, которая может поглотить тысячи Ньютонов». И Янош, не вняв предостережению своего отца, последовал его примеру. Уже в 1823 году он приходит к выводу, что Пятый постулат Евклида доказать невозможно, и пишет свой первый и единственный законченный трактат, где кратко и очень изящно излагает основы совершенно другой геометрии. «Я создал странный новый мир из ничего!», — так говорит он в письме своему отцу. В том же году Янош поступает офицером на военную службу и потом отдает ей 10 лет жизни. Янош Больяй был поистине гениальным молодым человеком — он знал девять языков (включая китайский!), играл на скрипке, прекрасно фехтовал и слыл отъявленным дуэлянтом.
Есть еще один человек, имя которого навсегда связанно с открытием новой неевклидовой геометрии. Его зовут Янош Больяй. Он был венгром, а Венгрия тогда принадлежала Австрийской империи. Еще в детстве Янош проявил способности к математике и музыке: к 10 годам он имел собственные музыкальные сочинения, а в 13 лет овладел уже основами дифференциального и интегрального исчислений. Его отец, Фракаш Больяй, сам был математиком и даже другом знаменитого Гаусса. Отец хотел, чтобы его сын учился у его великого друга, но вышло по-другому. В 20 лет Янош заканчивает военно-инженерную академию в Вене и тогда же увлекается теорией параллельных. Об этом он сообщает своему отцу и получает от него следующий красноречивый ответ: «Ты не должен пытаться одолеть теорию параллельных линий... я знаю этот путь, я прошел его до конца, я пережил эту беспросветную ночь, и всякий светоч, всякую радость жизни я похоронил в ней... Молю тебя: оставь в покое учение о параллельных — оно лишит тебя здоровья, досуга и покоя, оно погубит для тебя всю радость жизни». Согласитесь, после такого высокопарного предостережения трудно было сыну удержаться не заглянуть в эту «бездну, которая может поглотить тысячи Ньютонов». И Янош, не вняв предостережению своего отца, последовал его примеру. Уже в 1823 году он приходит к выводу, что Пятый постулат Евклида доказать невозможно, и пишет свой первый и единственный законченный трактат, где кратко и очень изящно излагает основы совершенно другой геометрии. «Я создал странный новый мир из ничего!», — так говорит он в письме своему отцу. В том же году Янош поступает офицером на военную службу и потом отдает ей 10 лет жизни. Янош Больяй был поистине гениальным молодым человеком — он знал девять языков (включая китайский!), играл на скрипке, прекрасно фехтовал и слыл отъявленным дуэлянтом.
Но история на этом не заканчивается. Волею судьбы его трактат под витиеватым названием «Приложение, содержащее науку о пространстве, не зависящую от истинности или ложности последней аксиомы Евклида» так и не был опубликован. Похоже, отец Яноша сам не мог его до конца понять, и потому не дал ему хода. А его сын все это время служил офицером в маленькой румынской крепости Тамешвар. Только через восемь лет отец решается послать трактат Яноша своему другу по университету — великому Гауссу. В письмах друзьям Гаусс называет юного Яноша гением высшего класса. А вот его ответ отцу юного гения был довольно холоден. Приведем его здесь: «Теперь несколько слов о работе Вашего сына. Вероятно, Вы будете немало поражены, если я начну с того, что не могу похвалить ее. Но я не могу сделать ничего иного, поскольку хвалить ее означало бы хвалить самого себя. Все содержание его работы, ее результаты и путь, на который встал Ваш сын, почти везде согласуются с моими собственными мыслями, которые занимали меня в течение последних 30 лет. Я имел намерение сам перенести их на бумагу, но не хотел ничего из этого публиковать при жизни. Ведь большинство людей совершенно не имеют понятия о том, о чем здесь идет речь. Поэтому я немало поражен тем, что освобожден от необходимости делать это сам, и меня радует, что именно сын моего старого друга предвосхитил меня». Таким образом, получалось, что молодой Янош просто прочитал мысли Гаусса!
 Ответ Гаусса нанес честолюбивому Яношу глубокую душевную рану. Его здоровье пошатнулось, характер сильно испортился, и в 1833 году Янош навсегда оставляет военную службу. Годом раньше его отец публикует книгу по математике, в приложении к которой помещает Appendix – трактат своего сына, написанный им на латыни. Трактат был наконец опубликован, но ни Янош, ни его отец не знали, что в далекой России еще в 1829-1830 годах в каком-то «Вестнике казанского университета» впервые были опубликованы результаты по неевклидовой геометрии Николая Ивановича Лобачевского.
Ответ Гаусса нанес честолюбивому Яношу глубокую душевную рану. Его здоровье пошатнулось, характер сильно испортился, и в 1833 году Янош навсегда оставляет военную службу. Годом раньше его отец публикует книгу по математике, в приложении к которой помещает Appendix – трактат своего сына, написанный им на латыни. Трактат был наконец опубликован, но ни Янош, ни его отец не знали, что в далекой России еще в 1829-1830 годах в каком-то «Вестнике казанского университета» впервые были опубликованы результаты по неевклидовой геометрии Николая Ивановича Лобачевского.
До конца своей жизни Янош Больяй занимался математикой, но так и не смог завершить и опубликовать больше ни одной своей работы. После его смерти было обнаружено несколько десятков тысяч черновиков. Более того, узнав о работах Лобачевского только в 1848 году, Янош Больяй пришел в ярость. До конца своей жизни он был уверен, что никакого Лобачевского не существует, а все его результаты присвоил и опубликовал «жадный» Гаусс. Правда, как истинного ученого, его восхитили некоторые теоремы и доказательства «Геометрических исследований» и он написал к ним подробные комментарии. Последние годы жизни этот гениальный человек провел в глубокой депрессии. Он много думал над тем, почему великие открытия совершаются разными людьми почти одновременно. В одном из его черновиков была найдена такая запись: «Для идей, как и для растений, настает время, когда они созревают в разных местах, подобно тому, как весной фиалки появляются везде, где светит солнце».
Николай Лобачевский, Янош Больяй, Карл Гаусс и Фридрих Швейкарт по праву считаются первооткрывателями неевклидовой геометрии. Но геометрия эта носит имя именно Лобачевского потому, что он первым опубликовал результаты своих исследований в печати. Запомните: для современного научного мира это имеет огромное значение! Но дело не только в этом. Николай Иванович Лобачевский не испугался насмешек современников, всеобщего непонимания и далеко продвинулся в построенной им теории. Он продолжал работу над ней до самой смерти. В конце жизни Лобачевский диктует свою Пангеометрию (то есть всеобщую геометрию), будучи уже слепым. Она была опубликована за год до его кончины в 1855 году в «Ученых записках Казанского университета». Эту последнюю свою работу Николай Иванович заканчивает вопросом о том, какова на самом деле природа окружающего нас пространства, то есть, каков этот мир – евклидов он или нет? И сам же отвечает на этот вопрос так: «Один только опыт может подтвердить истину данного предположения: например, измерением углов прямолинейного треугольника...».
Итак, один только опыт может подтвердить истину... Это вам ничего не напоминает? Конечно же! Данный подход — это основа физики, в которой эксперимент решает все. Получается, что геометрия — это тоже часть физики, то есть математическая теория, с помощью которой человек исследует данный ему мир. А каков этот мир, покажет только эксперимент. Так на самом деле и оказалось. Вскоре после смерти Лобачевского  появились первые модели неевклидовой геометрии. В 1856 году итальянский математик Эудженио Бельтрами обнаружил материальные тела, на поверхности которых выполняется геометрия Лобачевского. Одно из них — это так называемая псевдосфера, немного похожая на трубу старинного граммофона. Оказалось, что на этой поверхности через одну точку можно провести много «прямых» линий, не пересекающих данную «прямую». Само собой разумеется, «прямые» на такой кривой поверхности —
появились первые модели неевклидовой геометрии. В 1856 году итальянский математик Эудженио Бельтрами обнаружил материальные тела, на поверхности которых выполняется геометрия Лобачевского. Одно из них — это так называемая псевдосфера, немного похожая на трубу старинного граммофона. Оказалось, что на этой поверхности через одну точку можно провести много «прямых» линий, не пересекающих данную «прямую». Само собой разумеется, «прямые» на такой кривой поверхности —  это не прямые в обычном смысле этого слова. Так же как и на поверхности нашей Земли, такие «прямые» всегда идут по кратчайшему пути между своими точками — поэтому их и называют геодезическими.
это не прямые в обычном смысле этого слова. Так же как и на поверхности нашей Земли, такие «прямые» всегда идут по кратчайшему пути между своими точками — поэтому их и называют геодезическими.

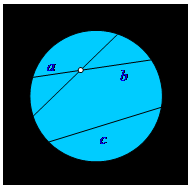 Еще через 15 лет немецким математиком Феликсом Клейном была обнаружена очень простая, но абстрактная модель неевклидовой геометрии. В этой модели вся плоскость — это внутренность некоторого круга, граница которого недостижима. Можно даже сказать, что это такая «круглая вселенная», на приближение к границе которой уходит бесконечное время. Точки в этой «вселенной» обыкновенные, отрезки тоже, а вот «прямые» — это отрезки, концы которых находятся на границе нашего круга. То есть дойти до «конца» такой «прямой» невозможно за конечное время. Очень легко проверить, что в этой круглой модели выполняются все аксиомы геометрии Евклида, кроме аксиомы параллельных. В самом деле: любые две ее точки можно соединить обычным отрезком, который можно продолжить до пересечения с границей нашего круга. То есть через любые две точки можно провести прямую. Из трех точек на прямой здесь тоже только одна лежит между двух других и любая прямая разбивает всю плоскость на две части так же, как в геометрии Евклида. Аксиомы откладывания отрезков и углов здесь тоже выполняются, если особым образом определить длину отрезка и величину угла. А вот аксиома параллельных в этой «круглой вселенной» не выполняется. Посмотрите на рисунок: на нем через точку М проходит много прямых, которые не пересекают данную прямую АВ. Таким образом, перед нами явная модель неевклидовой геометрии. Как жаль, что ни Лобачевский, ни Больяй, ни Швейкарт или Гаусс не могли увидеть ее при жизни!
Еще через 15 лет немецким математиком Феликсом Клейном была обнаружена очень простая, но абстрактная модель неевклидовой геометрии. В этой модели вся плоскость — это внутренность некоторого круга, граница которого недостижима. Можно даже сказать, что это такая «круглая вселенная», на приближение к границе которой уходит бесконечное время. Точки в этой «вселенной» обыкновенные, отрезки тоже, а вот «прямые» — это отрезки, концы которых находятся на границе нашего круга. То есть дойти до «конца» такой «прямой» невозможно за конечное время. Очень легко проверить, что в этой круглой модели выполняются все аксиомы геометрии Евклида, кроме аксиомы параллельных. В самом деле: любые две ее точки можно соединить обычным отрезком, который можно продолжить до пересечения с границей нашего круга. То есть через любые две точки можно провести прямую. Из трех точек на прямой здесь тоже только одна лежит между двух других и любая прямая разбивает всю плоскость на две части так же, как в геометрии Евклида. Аксиомы откладывания отрезков и углов здесь тоже выполняются, если особым образом определить длину отрезка и величину угла. А вот аксиома параллельных в этой «круглой вселенной» не выполняется. Посмотрите на рисунок: на нем через точку М проходит много прямых, которые не пересекают данную прямую АВ. Таким образом, перед нами явная модель неевклидовой геометрии. Как жаль, что ни Лобачевский, ни Больяй, ни Швейкарт или Гаусс не могли увидеть ее при жизни!

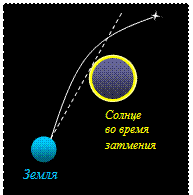 Ну а как же обстоит дело в нашей вселенной? Какова ее геометрия? В некоторой степени на этот вопрос смогла ответить теория относительности, созданная еще одним гением Альбертом Эйнштейном. Оказалось, что согласно этой теории, вблизи очень массивных тел лучи солнечного света должны искривляться. То есть прямые линии в поле очень сильной гравитации идут не так, как у Евклида. А ведь для человека путь луча света — это модель прямой линии. Получается, что само пространство должно искривляется силой тяготения! Как и любую физическую теорию, этот вывод необходимо было проверить на практике, то есть нужно было подтвердить его экспериментом. Эйнштейн пришел к своему открытию в 1916 году в разгар первой мировой войны, и необходимо было еще дождаться ее окончания, чтобы поставить такой опыт. Ведь провести его можно было только во время полного солнечного затмения. Идея эксперимента состояла в том, чтобы во время затмения сфотографировать звезду, которая по всем расчетам должна находиться позади Солнца, и которую невозможно в этот момент увидеть с Земли. Если же световые лучи, проходя вблизи огромного Солнца, на самом деле искривляются полем его гравитации, то они обогнут Солнце и звезду станет видно. Этот фантастический эксперимент был поставлен 29 мая 1919 года на маленьком острове возле западного побережья Африки и блестяще подтвердил догадку Эйнштейна! Видите, как сложно устроен мир, в котором мы с вами живем!
Ну а как же обстоит дело в нашей вселенной? Какова ее геометрия? В некоторой степени на этот вопрос смогла ответить теория относительности, созданная еще одним гением Альбертом Эйнштейном. Оказалось, что согласно этой теории, вблизи очень массивных тел лучи солнечного света должны искривляться. То есть прямые линии в поле очень сильной гравитации идут не так, как у Евклида. А ведь для человека путь луча света — это модель прямой линии. Получается, что само пространство должно искривляется силой тяготения! Как и любую физическую теорию, этот вывод необходимо было проверить на практике, то есть нужно было подтвердить его экспериментом. Эйнштейн пришел к своему открытию в 1916 году в разгар первой мировой войны, и необходимо было еще дождаться ее окончания, чтобы поставить такой опыт. Ведь провести его можно было только во время полного солнечного затмения. Идея эксперимента состояла в том, чтобы во время затмения сфотографировать звезду, которая по всем расчетам должна находиться позади Солнца, и которую невозможно в этот момент увидеть с Земли. Если же световые лучи, проходя вблизи огромного Солнца, на самом деле искривляются полем его гравитации, то они обогнут Солнце и звезду станет видно. Этот фантастический эксперимент был поставлен 29 мая 1919 года на маленьком острове возле западного побережья Африки и блестяще подтвердил догадку Эйнштейна! Видите, как сложно устроен мир, в котором мы с вами живем!
 Вопрос, поставленный Николаем Лобачевским в конце жизни, так и остается пока открытым. Даже если окружающее нас пространство искривлено, то заметить это на тех расстояниях, с которыми человек имеет дело, пока невозможно. Сам Лобачевский проводил такой эксперимент: он измерял углы треугольника, одна вершина которого находилась в определенной точке на Земле, вторая — на Солнце, а третья — на звезде Сириус. Данный его эксперимент не показал отличия от геометрии Евклида. Но это ничего не доказывает. Если на нашей земле нарисовать маленький треугольник со сторонами не больше 1 метра, то он тоже будет практически плоским, как у Евклида. Треугольник же со сторонами в 10000 км будет иметь совершенно другую форму и другую сумму своих углов. То есть даже на Земле на таких больших расстояниях должна работать уже другая геометрия! А расстояния в окружающей нас Вселенной вообще превосходят всякое воображение — ведь свет некоторых видимых нами звезд идет к нам от них миллионы лет!
Вопрос, поставленный Николаем Лобачевским в конце жизни, так и остается пока открытым. Даже если окружающее нас пространство искривлено, то заметить это на тех расстояниях, с которыми человек имеет дело, пока невозможно. Сам Лобачевский проводил такой эксперимент: он измерял углы треугольника, одна вершина которого находилась в определенной точке на Земле, вторая — на Солнце, а третья — на звезде Сириус. Данный его эксперимент не показал отличия от геометрии Евклида. Но это ничего не доказывает. Если на нашей земле нарисовать маленький треугольник со сторонами не больше 1 метра, то он тоже будет практически плоским, как у Евклида. Треугольник же со сторонами в 10000 км будет иметь совершенно другую форму и другую сумму своих углов. То есть даже на Земле на таких больших расстояниях должна работать уже другая геометрия! А расстояния в окружающей нас Вселенной вообще превосходят всякое воображение — ведь свет некоторых видимых нами звезд идет к нам от них миллионы лет!
___________________________________________________________________________
Решите задачи:
| 1. Попробуйте найти ошибку такого «доказательства» пятого постулата Евклида: Докажем, что через точку С проходит единственная прямая, параллельная АВ. Как известно, из точки С можно опустить единственный перпендикуляр СD на АВ. К прямой СD можно восстановить единственный перпендикуляр СЕ. Прямая СЕ параллельна АВ. Поскольку наши построения выполнены единственно возможным образом, то такая прямая только одна. | 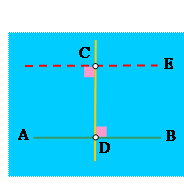
|
| 2. Как вы уже знаете, в геометрии Лобачевского через одну точку можно провести больше одной прямой, которые не пересекают данную. Докажите, что через любую точку в этой геометрии можно провести сколько угодно таких прямых. | 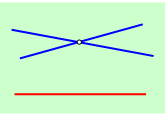
|
Пользуясь интернетом, ответьте на следующие вопросы:
| 1. Известно, что у Карла Гаусса и Николая Лобачевского был один учитель математики. Кто это был? |
| 2.Кто из первооткрывателей неевклидовой геометрии несколько лет преподавал в харьковском университете? |
| 3. Кто из первооткрывателей неевклидовой геометрии вызвал на дуэль родного отца? |
| 4.Обыватели часто полагают, что в геометрии Лобачевского параллельные прямые пересекаются. Как вы объясните, почему это не так? |
| 5.Кто из основателей неевклидовой геометрии лично наблюдал полное солнечное затмение? |
| 6.Определите, в каком произведении русской литературы так рассуждают о неевклидовой геометрии: «Объявляю, что принимаю Бога прямо и просто. Но вот, однако, что надо отметить: если Бог есть и если Он действительно создал землю, то, как нам совершенно известно, создал Он её по эвклидовой геометрии, а ум человеческий с понятием лишь о трёх измерениях пространства. Между тем находились и находятся даже и теперь геометры и философы и даже из замечательнейших, которые сомневаются в том, чтобы вся вселенная, или ещё обширнее, всё бытие было создано лишь по эвклидовой геометрии, осмеливаются даже мечтать, что две параллельные линии, которые по Эвклиду ни за что не могут сойтись на земле, может быть, и сошлись бы где-нибудь в бесконечности. Я, голубчик, решил так, что если я даже этого не могу понять, то где ж мне про Бога понять. Я смиренно сознаюсь, что у меня нет никаких способностей разрешать такие вопросы, у меня ум эвклидовский, земной, а потому где нам решать о том, чт́о не от мира сего.» Кто написал это произведение? |
[1] Отличить внутренние односторонние и накрест лежащие углы от других совсем нетрудно – те их стороны, которые лежат на секущей, всегда содержат ее отрезок, находящийся между двумя данными прямыми.
[2] Расстояние от точки до прямой – это длина самого короткого из отрезков, которым можно соединить данную точку с точками прямой линии. Через несколько параграфов мы с вами строго докажем, что самый короткий из этих отрезков – это отрезок перпендикуляра, опущенного из данной точки на прямую.