ЦЕНТР ПЕДАГОГИЧЕСКОГО МАСТЕРСТВА.
методические материалы проекта "Математическая вертикаль"
_____________________________________________________________________

ГЕОМЕТРИЯ: 7 класс
Параграф №14
Параллельные прямые
Автор: М.А. Волчкевич
 2018 г.
2018 г.
Аннотация: Данный материал представляет собой четырнадцатый параграф курса геометрии 7 класса для школ участников проекта "Математическая вертикаль". Он содержит признаки и свойства параллельных прямых, пятый постулат Евклида, а также различные его формулировки. В данном параграфе дается понятие транзитивности параллельности различных прямых и расстояния между параллельными. Кроме того, в нем рассказывается о истории возникновения неевклидовой геометрии. Материал рассчитан на 3-5 уроков в зависимости от начального уровня школьников.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
__________________________________________________________________________

 Параллельные прямые. Помните ли вы, что такое параллельныепрямые? В конце двадцатого века по телевизору можно было услышать забавную рекламу бытовой техники: «Параллельные прямые не пересекаются – доказано Евклидом. Надежная бытовая техника существует – доказано фирмой Z». У человека образованного такая реклама могла вызвать только улыбку. Ведь параллельные прямые не могут пересекаться просто по своему определению.
Параллельные прямые. Помните ли вы, что такое параллельныепрямые? В конце двадцатого века по телевизору можно было услышать забавную рекламу бытовой техники: «Параллельные прямые не пересекаются – доказано Евклидом. Надежная бытовая техника существует – доказано фирмой Z». У человека образованного такая реклама могла вызвать только улыбку. Ведь параллельные прямые не могут пересекаться просто по своему определению.
 Давайте вспомним: на плоскости две различные прямые либо пересекаются только в одной точке, либо вообще не пересекают друг друга. Тогда их и называют параллельными. Итак,
Давайте вспомним: на плоскости две различные прямые либо пересекаются только в одной точке, либо вообще не пересекают друг друга. Тогда их и называют параллельными. Итак,
Две различные прямые на плоскости называют
параллельными, если они не имеют общих точек.
 Слово параллельные на древнем греческом языке означало «проведенные около друг друга». А вот как длинно и тяжеловесно определял параллельные прямые сам Евклид: «Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не встречаются». Почему же Евклид так подробно дал это простое определение? Начнем с того, что слово «прямая» обозначало у Евклида обычный отрезок. Вот почему его нужно было мысленно продолжать в ту или другую сторону. Кроме того, для древних ученых само существование параллельных прямых было далеко неочевидным. По определению параллельные прямые должны лежать в одной плоскости. Но где на земле взять эту плоскость? Можно сделать плоский стол, ровный каменный пол в доме, городскую площадь, в конце концов. Но где на практике взять всю бесконечную плоскость? На Земле не может быть таких плоскостей. А раз так, то как проверить, что две прямые, проведенные на маленьком кусочке этой плоскости, никогда не пересекутся? Вдруг это произойдет через 100 километров от нашего чертежа или еще дальше? Конечно, Евклид не стал бы доказывать того, что параллельные прямые не пересекаются. Но он придумал, как проверить, что две данные прямые никогда не пересекутся, даже если их продолжать до бесконечности. Теорема об этом называется признаком параллельности двух прямых.
Слово параллельные на древнем греческом языке означало «проведенные около друг друга». А вот как длинно и тяжеловесно определял параллельные прямые сам Евклид: «Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той, ни с другой стороны между собой не встречаются». Почему же Евклид так подробно дал это простое определение? Начнем с того, что слово «прямая» обозначало у Евклида обычный отрезок. Вот почему его нужно было мысленно продолжать в ту или другую сторону. Кроме того, для древних ученых само существование параллельных прямых было далеко неочевидным. По определению параллельные прямые должны лежать в одной плоскости. Но где на земле взять эту плоскость? Можно сделать плоский стол, ровный каменный пол в доме, городскую площадь, в конце концов. Но где на практике взять всю бесконечную плоскость? На Земле не может быть таких плоскостей. А раз так, то как проверить, что две прямые, проведенные на маленьком кусочке этой плоскости, никогда не пересекутся? Вдруг это произойдет через 100 километров от нашего чертежа или еще дальше? Конечно, Евклид не стал бы доказывать того, что параллельные прямые не пересекаются. Но он придумал, как проверить, что две данные прямые никогда не пересекутся, даже если их продолжать до бесконечности. Теорема об этом называется признаком параллельности двух прямых.
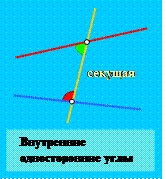
 Для того чтобы кратко сформулировать этот признак, нам с вами необходимо будет ввести несколько новых обозначений. Предположим, что две данные прямые пересекла некоторая третья прямая. Тогда эту прямую для краткости называют просто секущей. Секущая с двумя данными нам прямыми образует всего восемь углов. Пару углов, которые лежат по одну сторону от этой секущей так, как это показано на первом рисунке, называют внутренними односторонними углами. Другую пару углов на втором рисунке, которые лежат уже по разные стороны от секущей, называют накрест лежащими углами[1]. Всего же при пересечении двух прямых и секущей образуется две пары внутренних односторонних и две пары накрест лежащих углов. А еще одну пару углов, которые тоже лежат по одну сторону от секущей, называют соответственными. Эти углы показаны на третьем рисунке.
Для того чтобы кратко сформулировать этот признак, нам с вами необходимо будет ввести несколько новых обозначений. Предположим, что две данные прямые пересекла некоторая третья прямая. Тогда эту прямую для краткости называют просто секущей. Секущая с двумя данными нам прямыми образует всего восемь углов. Пару углов, которые лежат по одну сторону от этой секущей так, как это показано на первом рисунке, называют внутренними односторонними углами. Другую пару углов на втором рисунке, которые лежат уже по разные стороны от секущей, называют накрест лежащими углами[1]. Всего же при пересечении двух прямых и секущей образуется две пары внутренних односторонних и две пары накрест лежащих углов. А еще одну пару углов, которые тоже лежат по одну сторону от секущей, называют соответственными. Эти углы показаны на третьем рисунке.
 Теперь уже мы с вами готовы сформулировать первый признак параллельности двух прямых.
Теперь уже мы с вами готовы сформулировать первый признак параллельности двух прямых.
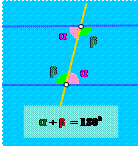
| ПЕРВЫЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ: Если секущая образует с двумя прямыми внутренние односторонние углы, сумма которых равна 1800, то эти прямые параллельны. | 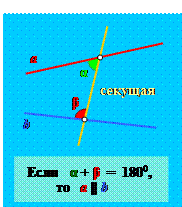
|
 Доказательство:
Доказательство:
Пусть секущая пересекает прямые a и b в точках А и В, образует с ними внутренние односторонние углы α и β, причем α + β = 1800. Вначале давайте найдем величину угла смежного с углом β. Поскольку сумма смежных углов всегда равна 1800, то величина этого угла будет равна 1800 – β = α. Точно также легко убедиться, что величина угла, смежного с углом α, будет равна β. Таким образом, с двух сторон от нашей секущей мы получим одинаковые пары внутренних односторонних углов α и β.

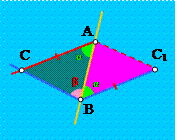
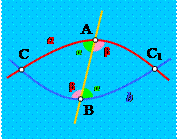 Давайте теперь докажем, что прямые a и b не могут пересекаться. Будем рассуждать от противного. Предположим, что прямые a и b не параллельны, то есть они пересекаются в некоторой точке С. Тогда с одной или с другой стороны от секущей обязательно получится треугольник АВС, два угла которого равны α и β.
Давайте теперь докажем, что прямые a и b не могут пересекаться. Будем рассуждать от противного. Предположим, что прямые a и b не параллельны, то есть они пересекаются в некоторой точке С. Тогда с одной или с другой стороны от секущей обязательно получится треугольник АВС, два угла которого равны α и β.
Построим теперь от луча ВА в другой полуплоскости угол, равный α, и на этом луче отложим отрезок ВС1 = АС. Сделать это всегда можно по аксиомам откладывания отрезков и углов. Тогда треугольники АВС1 и АВС будут равны по первому признаку. Значит, угол ВАС1 должен быть равен β. Получается, что углы САС1 и СВС1 должны быть развернутыми, поскольку величина каждого из них равна α + β = 1800. Но тогда точки С, А и С1 должны лежать на одной прямой. И то же самое можно сказать и про точки С, В и С1. Выходит, что через точки С и С1 проходят две различные прямые. А это невозможно по первому свойству прямой линии. Мы получили противоречие с аксиомой. А раз так, то наше предположение о пересечении прямых a и b в некоторой точке С оказалось неверным. Поэтому такой точки не может быть. То есть прямые a и b параллельны. Что и требовалось доказать.
Итак, признак параллельности двух прямых доказан. Мы с вами сформулировали его так же, как Евклид, через сумму внутренних односторонних углов при секущей. Однако часто этот признак формулируют и по-другому. Мы приведем здесь еще две самые известные его формулировки:
ДРУГИЕ ФОРМУЛИРОВКИ ПРИЗНАКА
ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ:
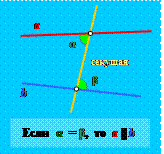
 1) Если секущая образует с двумя прямыми
равные накрест лежащие углы,
то эти прямые параллельны. 1) Если секущая образует с двумя прямыми
равные накрест лежащие углы,
то эти прямые параллельны.
| 
|
| 2) Если соответственные углы при двух прямых и секущей равны, то эти прямые параллельны. | 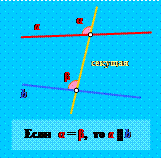
|

Упражнение 1: Покажите, что две другие формулировки признака параллельных
прямых равнозначны главному признаку параллельных.
 Так почему же через точку, которая не лежит на данной прямой, всегда можно провести параллельную ей прямую? Теперь понять это уже легко. Пусть точка М не лежит на прямой а. Давайте возьмем на этой прямой любую точку К и соединим ее отрезком с точкой М. Если теперь на данной прямой взять любую другую точку А, то мы сразу получим угол АКМ с некоторой величиной α. По аксиоме откладывания углов от луча КМ в другой полуплоскости относительно прямой КМ всегда можно отложить угол ВМК с такой же величиной α. Тогда около прямой МК мы получим равные накрест лежащие углы АКМ и ВКМ. Значит прямая ВМ должна быть параллельна прямой а по признаку. То есть искомая прямая ВМ существует.
Так почему же через точку, которая не лежит на данной прямой, всегда можно провести параллельную ей прямую? Теперь понять это уже легко. Пусть точка М не лежит на прямой а. Давайте возьмем на этой прямой любую точку К и соединим ее отрезком с точкой М. Если теперь на данной прямой взять любую другую точку А, то мы сразу получим угол АКМ с некоторой величиной α. По аксиоме откладывания углов от луча КМ в другой полуплоскости относительно прямой КМ всегда можно отложить угол ВМК с такой же величиной α. Тогда около прямой МК мы получим равные накрест лежащие углы АКМ и ВКМ. Значит прямая ВМ должна быть параллельна прямой а по признаку. То есть искомая прямая ВМ существует.
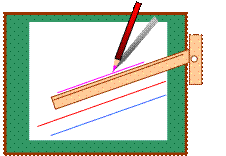
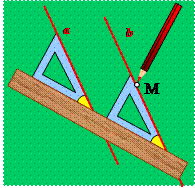 Существует множество практических способов для проведения параллельных прямых с помощью различных инструментов. Давайте посмотрим, как с помощью линейки и чертежного угольника можно проводить прямые, параллельные данной. Чтобы провести через точку М прямую, параллельную прямой а, нужно приложить к этой прямой чертежный угольник, а к нему линейку так, как это показано на рисунке. Потом необходимо сдвигать угольник вдоль этой линейки, пока точка М не окажется на той его стороне, которая была приложена к прямой а. Вдоль этой стороны и проводят нужную прямую b. Прямые а и b будут параллельны по первому признаку, поскольку образуют с линейкой равные соответственные углы. Похожим способом параллельные прямые можно проводить с помощью чертежной рейсшины.
Существует множество практических способов для проведения параллельных прямых с помощью различных инструментов. Давайте посмотрим, как с помощью линейки и чертежного угольника можно проводить прямые, параллельные данной. Чтобы провести через точку М прямую, параллельную прямой а, нужно приложить к этой прямой чертежный угольник, а к нему линейку так, как это показано на рисунке. Потом необходимо сдвигать угольник вдоль этой линейки, пока точка М не окажется на той его стороне, которая была приложена к прямой а. Вдоль этой стороны и проводят нужную прямую b. Прямые а и b будут параллельны по первому признаку, поскольку образуют с линейкой равные соответственные углы. Похожим способом параллельные прямые можно проводить с помощью чертежной рейсшины.
 Аксиома параллельных. Среди всех аксиом Евклида была одна, которая две тысячи лет не давала покоя множеству математиков. Ее называли «пятном на сочинениях Евклида» и пытались доказать как теорему, то есть вывести из других его аксиом. В списке геометрических постулатов Евклида это был его последний, так называемый пятый постулат. Дело в том, что данная аксиома не была так очевидна, как другие, и сложно формулировалась. Видимо, сам Евклид это понимал и старался как можно позже начать пользоваться данным постулатом в изложении своей теории. Так что же это была за аксиома? Давайте вначале приведем ее формулировку, данную самим Евклидом: «Если прямая, падающая на две прямые, образует по одну сторону внутренние углы, в сумме меньшие двух прямых углов, то продолженные неограниченно эти две прямые встретятся с той стороны, где расположены данные углы». На современный язык это можно перевести так:
Аксиома параллельных. Среди всех аксиом Евклида была одна, которая две тысячи лет не давала покоя множеству математиков. Ее называли «пятном на сочинениях Евклида» и пытались доказать как теорему, то есть вывести из других его аксиом. В списке геометрических постулатов Евклида это был его последний, так называемый пятый постулат. Дело в том, что данная аксиома не была так очевидна, как другие, и сложно формулировалась. Видимо, сам Евклид это понимал и старался как можно позже начать пользоваться данным постулатом в изложении своей теории. Так что же это была за аксиома? Давайте вначале приведем ее формулировку, данную самим Евклидом: «Если прямая, падающая на две прямые, образует по одну сторону внутренние углы, в сумме меньшие двух прямых углов, то продолженные неограниченно эти две прямые встретятся с той стороны, где расположены данные углы». На современный язык это можно перевести так:
| АКСИОМА ПАРАЛЛЕЛЬНЫХ: (формулировка Евклида) Если секущая образует с двумя прямыми внутренние односторонние углы, сумма которых меньше 1800, то эти прямые пересекутся в той полуплоскости, где расположены данные углы. | 
|
В такой формулировке ясно, что аксиома параллельных – это утверждение, которое является обратным к признаку параллельных прямых. Скорее всего, Евклид сам пытался его доказать, не смог этого сделать и оставил в виде аксиомы. Многие математики «доказывали» пятый постулат Евклида, но в их доказательствах всегда потом находили ошибки. Каждый раз оказывалось, что в ходе очередного «доказательства» незаметно был использован какой-то совершенно очевидный факт, которого тем не менее нет в списке аксиом Евклида. А значит, с математической точки зрения это доказательство незаконно. Со временем накопился целый список из таких очевидных утверждений, каждое из которых может заменить собою аксиому параллельных прямых. В конце данного параграфа вы можете найти несколько утверждений из этого списка. Но самое известное из них мы приведем сейчас. Оно принадлежит греческому математику Проклу, который работал в Александрии в 4 веке нашей эры. Вот как оно звучит:
| АКСИОМА ПАРАЛЛЕЛЬНЫХ: (современная формулировка) Через точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной. | 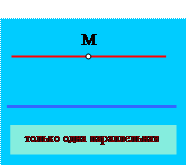
|
 Такая формулировка аксиомы параллельных теперь считается общепринятой. Она очевидна, легко запоминается и на первый взгляд никак не связана со старинной формулировкой, данной Евклидом. Мы же с вами сейчас убедимся, что оба этих утверждения говорят об одном и том же.
Такая формулировка аксиомы параллельных теперь считается общепринятой. Она очевидна, легко запоминается и на первый взгляд никак не связана со старинной формулировкой, данной Евклидом. Мы же с вами сейчас убедимся, что оба этих утверждения говорят об одном и том же.
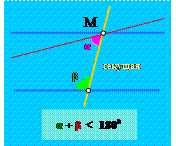 Действительно, пусть две прямые с одной стороны от секущей образовали внутренние углы, сумма которых равна 1800. Тогда, как вы знаете, эти прямые должны быть параллельны по первому признаку. Но легко заметить, что с другой стороны от секущей сумма внутренних углов при этих прямых также должна быть равна 1800.
Действительно, пусть две прямые с одной стороны от секущей образовали внутренние углы, сумма которых равна 1800. Тогда, как вы знаете, эти прямые должны быть параллельны по первому признаку. Но легко заметить, что с другой стороны от секущей сумма внутренних углов при этих прямых также должна быть равна 1800.
Проведем теперь через точку М пересечения секущей с одной из наших параллельных прямых любую другую прямую – на рисунке она показана красным цветом. Посмотрите: либо с одной, либо с другой стороны от секущей новая прямая со второй из параллельных будет образовывать углы, сумма которых будет меньше 1800. Тогда она обязана пересечь вторую из этих параллельных прямых по знаменитому пятому постулату Евклида. Значит, через точку М нельзя провести больше ни одной прямой параллельно данной. То есть такая прямая единственная. Так мы с вами убедились, что из старинной формулировки Евклида следует современная.

Упражнение 2: Покажите, что из современной формулировки аксиомы
параллельных прямых следует Пятый постулат Евклида.
А что вытекает из знаменитого Пятого постулата Евклида, зачем он вообще нужен?
Коротко ответить можно так: данная аксиома определяет «плоскую» геометрию, у которой нет никакой «кривизны». Из этой аксиомы также следует, что сумма углов любого треугольника на плоскости одинакова и равна 1800. Но чтобы проверить это исключительно важное свойство плоскости, вначале нам потребуется доказать свойство параллельных прямых.
| ПЕРВОЕ СВОЙСТВО ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: Если две прямые параллельны, то любая секущая образует с ними равные накрест лежащие углы. | 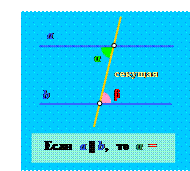
|
 Доказательство: Пусть прямые a и b параллельны и некоторая секущая пересекает их в точках А и В. Будем опять рассуждать от противоположного: допустим, что эта секущая образует с прямыми a и b накрест лежащие углы α и β, которые не равны друг другу. Пусть, например, α > β.
Доказательство: Пусть прямые a и b параллельны и некоторая секущая пересекает их в точках А и В. Будем опять рассуждать от противоположного: допустим, что эта секущая образует с прямыми a и b накрест лежащие углы α и β, которые не равны друг другу. Пусть, например, α > β.
Давайте теперь проведем через точку А еще одну прямую а 1 так, чтобы угол между ней и прямой АВ был в точности равен β. Тогда прямые а 1 и b должны быть параллельны по признаку, поскольку секущая АВ образует с ними равные накрест лежащие углы. Но тогда получается, что через точку А кроме прямой a, проходит еще одна прямая а 1, также параллельная прямой b. А вот это уже противоречит аксиоме параллельных. Полученное противоречие и показывает, что накрест лежащие углы при двух параллельных и секущей всегда должны быть равными. Что и требовалось доказать.
Как и в случае с признаком, у данного свойства параллельных тоже есть другие формулировки. Все они являются утверждениями, обратными к своим признакам. Вот как они звучат:

ДРУГИЕ ФОРМУЛИРОВКИ СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:
1) Если две прямые параллельны, то сумма внутренних односторонних углов при любой секущей равна 1800.
2) Если две прямые параллельны, то при любой секущей соответственные углы равны

Упражнение 3: Нарисуйте нужные чертежи и покажите, что две другие формулировки
свойства параллельных равнозначны первому их свойству.
 Транзитивность параллельности. Пусть у нас есть две параллельные прямые. Давайте проведем третью прямую параллельно одной из них. Будет ли она параллельна второй прямой? «Конечно, – скажете вы, – это же очевидно, то есть в прямом смысле слова видно нашими глазами!». Но как вы уже знаете, в геометрии все очевидные вещи либо вообще берут на веру и тогда их называют аксиомами, либо строго доказывают. В данном случае мы имеем дело с утверждением о параллельности прямых линий, которую называют транзитивностью. И мы с вами строго его докажем.
Транзитивность параллельности. Пусть у нас есть две параллельные прямые. Давайте проведем третью прямую параллельно одной из них. Будет ли она параллельна второй прямой? «Конечно, – скажете вы, – это же очевидно, то есть в прямом смысле слова видно нашими глазами!». Но как вы уже знаете, в геометрии все очевидные вещи либо вообще берут на веру и тогда их называют аксиомами, либо строго доказывают. В данном случае мы имеем дело с утверждением о параллельности прямых линий, которую называют транзитивностью. И мы с вами строго его докажем.
 Что такое транзитивность? Объяснить это проще всего на примерах. Предположим, в вашем классе есть два ученика, которые с вами сейчас одного роста. Можно ли утверждать, что их рост одинаковый? «Конечно, можно!» – скажете вы. Вот это и есть транзитивность. То же самое можно сказать о размере вашей обуви или, допустим, цвете ваших волос. Можно даже сказать, что совпадение роста двух учеников передается от одного из них к другому через вас. Вы являетесь как бы посредником при передаче этого равенства между двумя другими учениками. Вообще любое отношение равенства, очевидно, должно обладать транзитивностью.
Что такое транзитивность? Объяснить это проще всего на примерах. Предположим, в вашем классе есть два ученика, которые с вами сейчас одного роста. Можно ли утверждать, что их рост одинаковый? «Конечно, можно!» – скажете вы. Вот это и есть транзитивность. То же самое можно сказать о размере вашей обуви или, допустим, цвете ваших волос. Можно даже сказать, что совпадение роста двух учеников передается от одного из них к другому через вас. Вы являетесь как бы посредником при передаче этого равенства между двумя другими учениками. Вообще любое отношение равенства, очевидно, должно обладать транзитивностью.
Или возьмем другой пример. Предположим, что вы ростом немного выше Пети, зато Ваня выше вас на целую голову. Верно ли, что Ваня тогда будет выше Пети? «А как же может быть иначе?» – скажете вы. Все правильно. Дело в том, что такое понятие, как «быть больше» тоже обладает транзитом. Это нам с вами подсказывает наш человеческий опыт. А само слово «транзитивность» образовалось от латинского глагола transit, что означает «проходить» или «передавать». «Sic transit gloria mundi» – эта фраза на древней латыни вот уже две тысячи лет гласит: «Так проходит земная слава!».

Упражнение 4: В арифметике тоже есть транзитивность. Объясните ее на примере
делимости целых чисел на три.
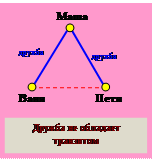 Однако далеко не все отношения между объектами или даже людьми обладают транзитивностью. Если вы дружите с двумя ребятами, то они вовсе не обязаны дружить между собой. Два ваших друга могут даже не знать один о другом. Значит, отношение дружбы не обладает транзитивностью. То же самое можно сказать про вражду или знакомство. Конечно, в геометрии тоже есть такие примеры. Если две прямые одновременно перпендикулярны к третьей прямой, то между собой эти прямые вовсе не будут перпендикулярны – они будут параллельны. Значит, отношение перпендикулярности двух прямых тоже не обладает транзитивностью.
Однако далеко не все отношения между объектами или даже людьми обладают транзитивностью. Если вы дружите с двумя ребятами, то они вовсе не обязаны дружить между собой. Два ваших друга могут даже не знать один о другом. Значит, отношение дружбы не обладает транзитивностью. То же самое можно сказать про вражду или знакомство. Конечно, в геометрии тоже есть такие примеры. Если две прямые одновременно перпендикулярны к третьей прямой, то между собой эти прямые вовсе не будут перпендикулярны – они будут параллельны. Значит, отношение перпендикулярности двух прямых тоже не обладает транзитивностью.
А вот параллельность различных прямых обладает транзитом, то есть передается через «посредника» – третью прямую. Давайте сформулируем теперь это строго:
| ТРАНЗИТИВНОСТЬ ПАРАЛЛЕЛЬНОСТИ: Если две различные прямые параллельны третьей прямой, то они параллельны между собой. | 
|
Доказательство: Пусть различные прямые а и b одновременно параллельны некоторой прямой с. Давайте докажем, что прямые а и b должны быть параллельны между собой. Будем рассуждать от противоположного. Допустим, что прямые а и b не параллельны. Тогда они по определению должны пересекаться в некоторой точке М.
 Посмотрите на получившийся чертеж внимательно – вы ничего не замечаете? Конечно же, на нем через одну точку М проходят сразу две прямые, параллельные прямой с! То есть это противоречит аксиоме параллельных. Значит, наличие самой точки М пересечения прямых а и b противоречит аксиоме. Получается, что такой точки нет, то есть прямые а и b должны быть параллельны между собой. Что и требовалось доказать.
Посмотрите на получившийся чертеж внимательно – вы ничего не замечаете? Конечно же, на нем через одну точку М проходят сразу две прямые, параллельные прямой с! То есть это противоречит аксиоме параллельных. Значит, наличие самой точки М пересечения прямых а и b противоречит аксиоме. Получается, что такой точки нет, то есть прямые а и b должны быть параллельны между собой. Что и требовалось доказать.
Мы только что с вами доказали транзитивность параллельности прямых, опираясь на Пятый постулат Евклида. Если же принять транзит параллельности прямых без доказательства, как аксиому, то из него можно легко получить аксиому параллельных.

Упражнение 5: Покажите, как из транзита параллельности прямых следует пятый
постулат Евклида.
Получается, что Пятый постулат Евклида и транзит параллельности прямых – это одно и тоже. То есть, каждое из этих утверждений можно вывести из другого. Математики в таких случаях говорят, что такие утверждения равнозначны или эквивалентны. В конце параграфа вы сможете прочитать про другие утверждения, которые также эквивалентны знаменитому Пятому постулату Евклида. Любое из них определяет плоскую геометрию Евклида, где через одну точку можно провести не больше одной прямой, параллельной данной.
























 Свойство полосы. На что похожа пара параллельных прямых? Конечно, на рельсы поезда, прямую лыжню, на двойную сплошную линию на дороге или следы от колес проехавшей телеги. Древние греки думали также — не зря они назвали такие прямые «идущими рядом». Правда, подобное сравнение будет удачным только в случае, когда поезд или та же телега сами движутся по прямой линии. А на что похожа часть плоскости, расположенная между параллельными прямыми? Конечно же, на бесконечную полосу. С похожими полосами, только конечной длины, все мы имеем дело в жизни: любая лента, тесьма или ковровая дорожка, разложенные на плоскость, дадут нам такую полосу.
Свойство полосы. На что похожа пара параллельных прямых? Конечно, на рельсы поезда, прямую лыжню, на двойную сплошную линию на дороге или следы от колес проехавшей телеги. Древние греки думали также — не зря они назвали такие прямые «идущими рядом». Правда, подобное сравнение будет удачным только в случае, когда поезд или та же телега сами движутся по прямой линии. А на что похожа часть плоскости, расположенная между параллельными прямыми? Конечно же, на бесконечную полосу. С похожими полосами, только конечной длины, все мы имеем дело в жизни: любая лента, тесьма или ковровая дорожка, разложенные на плоскость, дадут нам такую полосу.








 Каждый человек по опыту знает, что противоположные края у ленты или ковровой дорожки параллельны, а ее ширина всюду одинакова. Вот только почему это так? Давайте вспомним, как вообще измеряют ширину полосы. Обычно перпендикулярно к ее краю прикладывают линейку и смотрят, какой отрезок этой линейки окажется внутри полосы. Длину данного отрезка и считают расстоянием между краями полосы или ее шириной.
Каждый человек по опыту знает, что противоположные края у ленты или ковровой дорожки параллельны, а ее ширина всюду одинакова. Вот только почему это так? Давайте вспомним, как вообще измеряют ширину полосы. Обычно перпендикулярно к ее краю прикладывают линейку и смотрят, какой отрезок этой линейки окажется внутри полосы. Длину данного отрезка и считают расстоянием между краями полосы или ее шириной.
 Можно, конечно, свернуть ленту в рулон и измерить высоту полученного цилиндра. Будет то же самое. Только почему ширина любой полосы всюду одинакова? А дело в том, что с этим связано еще одно важное свойство параллельных прямых.
Можно, конечно, свернуть ленту в рулон и измерить высоту полученного цилиндра. Будет то же самое. Только почему ширина любой полосы всюду одинакова? А дело в том, что с этим связано еще одно важное свойство параллельных прямых.
| ВТОРОЕ СВОЙСТВО ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: Длина перпендикуляра, опущенного из любой точки прямой линии на параллельную ей прямую, постоянна. Длину такого перпендикуляра называют расстоянием между параллельными прямыми или шириной полосы между ними. | 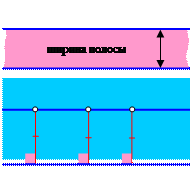
|
 Доказательство: Возьмем две параллельные прямые и на одной из них отметим две произвольные точки А и В. Опустим из них перпендикуляры АА1 и ВВ1 на параллельную прямую. Давайте докажем, что АА1 = ВВ1. Для этого проведем отрезок А1В и рассмотрим треугольники АА1В и А1ВВ1. В самом деле, прямые АА1 и ВВ1 одновременно перпендикулярны одной прямой, поэтому должны быть параллельны друг другу по первому признаку параллельных. Значит, по первому свойству параллельных они образуют с секущей А1В равные накрест лежащие углы АА1В и В1ВА1. А так как сами прямые АВ и А1В1 параллельны по условию, то они тоже образуют с секущей А1В равные накрест лежащие углы АВА1 и В1А1В. Но тогда треугольники АА1В и А1ВВ1 должны быть равны по второму признаку, поскольку имеют общую сторону А1В и два прилегающих к ней равных угла. Поэтому АА1 = ВВ1. Получается, что длина перпендикуляра, опущенного из любой точки В нашей прямой на параллельную ей прямую, равна отрезку АА1, то есть она постоянна. Что и требовалось доказать.
Доказательство: Возьмем две параллельные прямые и на одной из них отметим две произвольные точки А и В. Опустим из них перпендикуляры АА1 и ВВ1 на параллельную прямую. Давайте докажем, что АА1 = ВВ1. Для этого проведем отрезок А1В и рассмотрим треугольники АА1В и А1ВВ1. В самом деле, прямые АА1 и ВВ1 одновременно перпендикулярны одной прямой, поэтому должны быть параллельны друг другу по первому признаку параллельных. Значит, по первому свойству параллельных они образуют с секущей А1В равные накрест лежащие углы АА1В и В1ВА1. А так как сами прямые АВ и А1В1 параллельны по условию, то они тоже образуют с секущей А1В равные накрест лежащие углы АВА1 и В1А1В. Но тогда треугольники АА1В и А1ВВ1 должны быть равны по второму признаку, поскольку имеют общую сторону А1В и два прилегающих к ней равных угла. Поэтому АА1 = ВВ1. Получается, что длина перпендикуляра, опущенного из любой точки В нашей прямой на параллельную ей прямую, равна отрезку АА1, то есть она постоянна. Что и требовалось доказать.
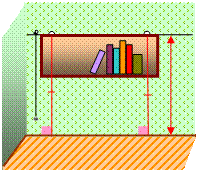
Знаете, как плотники или строители проводят параллельные линии? Наивно думать, что для этого они каждый раз проводят секущую прямую и откладывают от нее равные накрест лежащие углы. На практике это было бы слишком сложно. Вспомните, как у вас дома вешают обыкновенные полки. Чтобы полка висела горизонтально, она должна быть параллельна полу — иначе предметы с нее будут падать. А как проще всего добиться этой параллельности? Все правильно: точки крепления полки к стене нужно отметить на одинаковой высоте над полом, тогда ваша полка будет висеть «прямо», а не «криво». Расстояние до пола обычно вычисляют по длине отвеса или перпендикуляра к нижнему краю стены. Знаете, почему так делают? Это простое правило связано с еще одним признаком параллельных прямых, с которым мы с вами сейчас познакомимся.
| ВТОРОЙ ПРИЗНАК ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: Если две точки одной прямой лежат по одну сторону от другой прямой и находятся на одинаковых расстояниях от нее, то эти две прямые параллельны. | 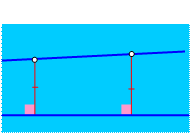
|
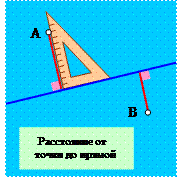
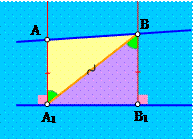 Доказательство: Пусть точки А и В находятся с одной стороны от прямой l на равных от нее расстояниях. Напомним, что расстоянием от точки до прямой считают[2] длину отрезка перпендикуляра, опущенного из нее на эту прямую l. Итак, пусть АА1 и ВВ1 — два таких перпендикуляра, проведенных из точек А и В к прямой l. По условию они равны, то есть АА1 = ВВ1. Давайте докажем, что прямые АВ и l параллельны. Для этого опять проведем отрезок А1В и рассмотрим треугольники АА1В и А1ВВ1. Так как прямые АА1 и ВВ1 одновременно перпендикулярны прямой l, то они должны быть параллельны друг другу по признаку. Тогда по первому свойству параллельных они образуют с секущей А1В равные накрест лежащие углы АА1В и В1ВА1. Значит треугольники АА1В и А1ВВ1 должны быть равны по первому признаку, поскольку АА1 = ВВ1, сторона А1В у них общая, а углы между этими сторонами равны. Поэтому в этих треугольниках равны углы АВА1 и ВА1В1. Но эти углы накрест лежащие при прямых АВ, l и секущей. Значит, прямая АВ должна быть параллельна прямой l по первому признаку параллельных. Что и требовалось доказать.
Доказательство: Пусть точки А и В находятся с одной стороны от прямой l на равных от нее расстояниях. Напомним, что расстоянием от точки до прямой считают[2] длину отрезка перпендикуляра, опущенного из нее на эту прямую l. Итак, пусть АА1 и ВВ1 — два таких перпендикуляра, проведенных из точек А и В к прямой l. По условию они равны, то есть АА1 = ВВ1. Давайте докажем, что прямые АВ и l параллельны. Для этого опять проведем отрезок А1В и рассмотрим треугольники АА1В и А1ВВ1. Так как прямые АА1 и ВВ1 одновременно перпендикулярны прямой l, то они должны быть параллельны друг другу по признаку. Тогда по первому свойству параллельных они образуют с секущей А1В равные накрест лежащие углы АА1В и В1ВА1. Значит треугольники АА1В и А1ВВ1 должны быть равны по первому признаку, поскольку АА1 = ВВ1, сторона А1В у них общая, а углы между этими сторонами равны. Поэтому в этих треугольниках равны углы АВА1 и ВА1В1. Но эти углы накрест лежащие при прямых АВ, l и секущей. Значит, прямая АВ должна быть параллельна прямой l по первому признаку параллельных. Что и требовалось доказать.
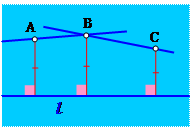
Давайте теперь с одной стороны от прямой l возьмем три любые точки, расстояние от которых до этой прямой одинаково. Будут ли все эти точки лежать на одной прямой? Конечно, — скажете вы, как же может быть по-другому? Так оно и есть, а связано это опять с аксиомой параллельных. В самом деле, если расстояния от точек А, В и С до прямой l равны, то по только что доказанному признаку прямые АВ и ВС должны быть параллельны прямой l. Но по аксиоме параллельных через точку В можно провести только одну прямую, параллельную l. Поэтому прямые АВ и ВС должны совпасть. А это значит, что точка С лежит на прямой АВ. Поскольку точка С была выбрана нами произвольно, то
| Все точки, расположенные по одну сторону от данной прямой и находящиеся от нее на одинаковом расстоянии образуют прямую, параллельную прямой l. |
В данной полуплоскости относительно прямой l других таких точек нет.
| Упражнение 6. На листе бумаги проведите прямую линию, не параллельную краям листа. Без циркуля и линейки, только складывая эту бумагу, получите на ней прямую, параллельную нарисованной. | 
|
| Упражнение 7. С помощью листа бумаги формата А4 изготовьте квадрат со стороной 21 см. Постройте в нем точку так, чтобы расстояния от нее до сторон квадрата были равны 8 см и 13 см. Верно ли, что эта точка лежит на диагонали квадрата? | 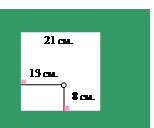
|
| Упражнение 8. Возьмите лист бумаги формата А4. Проведите диагональ этого прямоугольника. А теперь постройте на нем все точки на расстоянии 10 см от этой диагонали. | 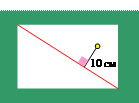
|
Ответьте на вопросы:
| 1. Какие прямые называются параллельными? |
| 2.Какие вы знаете признаки параллельных прямых? |
| 3. Что называется расстоянием от точки до прямой? |
| 4.Как Евклид формулировал свой Пятый постулат? |
| 4.Как звучит современная формулировка аксиомы параллельных прямых? |
| 5. Что такое транзитивность параллельности прямых? |
| 6. Где находятся все точки по одну сторону от прямой на равном от нее расстоянии? |
| 7.Какие вы знаете геометрические отношения, которые не обладают транзитивностью? |
| 8.Какие вы знаете отношения «из жизни», которые не обладают транзитивностью? |
| 9.На чем основан практический способ проведения параллельных прямых с помощью чертежной рейсшины? |
| 10.Две точки одной прямой находятся на равных расстояниях от другой прямой. Обязательно ли эти прямые параллельны? |
Давайте теперь с вами решим несколько задач.
 _____________________________________________________________________________
_____________________________________________________________________________
Задача 1. Прямая пересекает две параллельные в точках А и В. Биссектрисы двух смежных углов с вершиной в точке В при одной из этих прямых пересекают другую параллельную прямую в точках С и Е. Докажите, что АС = АЕ.
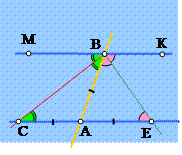 Решение: Угол АСВ равенуглу МВС, поскольку они накрест лежащие при двух параллельных и секущей ВС. Поэтому углы АСВ и АВС равны. Значит треугольник АВС равнобедренный по признаку, то есть АС = АВ. Также легко понять, что и треугольник АВЕ тоже равнобедренный. Поэтому АЕ = АВ. Таким образом, АС = АЕ. Что и требовалось доказать.
Решение: Угол АСВ равенуглу МВС, поскольку они накрест лежащие при двух параллельных и секущей ВС. Поэтому углы АСВ и АВС равны. Значит треугольник АВС равнобедренный по признаку, то есть АС = АВ. Также легко понять, что и треугольник АВЕ тоже равнобедренный. Поэтому АЕ = АВ. Таким образом, АС = АЕ. Что и требовалось доказать.
 _____________________________________________________________________________
_____________________________________________________________________________
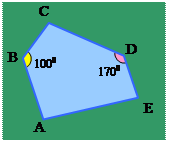
 Задача 2. В пятиугольнике АВСDE стороны АВ и DE параллельны, а углы АВС и СDE равны 1000 и 1200. Найдите величину угла ВСD.
Задача 2. В пятиугольнике АВСDE стороны АВ и DE параллельны, а углы АВС и СDE равны 1000 и 1200. Найдите величину угла ВСD.
Решение: Проведем через точку С прямую CF параллельно прямым АВ и DЕ. Тогда углы АВС и ВСF будут внутренними односторонними при параллельных АВ и СF и секущей ВС. Поэтому их сумма должна быть равна 1800. Значит, угол ВСF равен 1800 – 1000 = 800. Точно также угол DCF окажется равен 1800 – 1200 = 600. Таким образом искомый угол ВСD равен 800 + 600 = 1400. Ответ: 1400 ____________________________________________________________________________
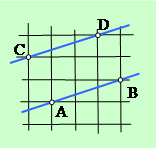
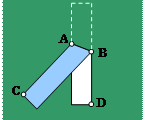
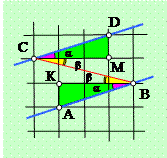 Задача 3. Докажите, что прямые АВ и СD на рисунке клетчатой бумаги параллельны.
Задача 3. Докажите, что прямые АВ и СD на рисунке клетчатой бумаги параллельны.
Решение: Отметим точки М и К на чертеже и проведем отрезок ВС. Треугольники МDС и ВАВ равны по двум сторонам и прямому углу между ними, поэтому угол МСD равен углу КВА. Обозначим их величину буквой α.
Кроме того, прямые СМ и ВК параллельны, поэтому углы МСВ и КВС равны как накрест лежащие при них и секущей ВС. Их величину мы обозначим буквой β. Тогда величина углов DСВ и АВС равна α + β. Поскольку эти углы равны и являются накрест лежащими при секущей ВС, то прямые АВ и СD параллельны по первому признаку. Что и требовалось доказать. ____________________________________________________________________________
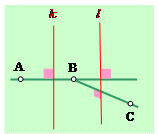
 Задача 4. К каждой стороне неразвернутого угла провели перпендикулярную прямую. Докажите, что эти перпендикуляры пересекаются.
Задача 4. К каждой стороне неразвернутого угла провели перпендикулярную прямую. Докажите, что эти перпендикуляры пересекаются.
Решение: Давайте рассуждать от противоположного. Предположим, что два перпендикуляра, проведенных к сторонам данного угла АВС не пересекаются. Тогда они должны быть параллельны. Нарисуем их, как две параллельные прямые k и l. Прямая АВ перпендикулярна прямой k, поэтому по первому свойству параллельных она должна быть также перпендикулярна и прямой l. Но прямая ВС также перпендикулярна прямой l по условию. Тогда по признаку прямые АВ и ВС должны быть параллельны. Но эти прямые имеют общую точку В, чего не может быть по определению. Мы получили противоречие. Значит, прямые k и l не могут быть параллельны, то есть они пересекаются. Что и требовалось доказать.
___________________________________________________________________________
Решите задачи:
| 1. Параллельно стороне равнобедренного треугольника провели прямую. Докажите, что она отсекает от него тоже равнобедренный треугольник. | 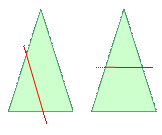
|
| 2. Через точку на биссектрисе угла параллельно его сторонам провели две прямые. Они отсекают от данного угла четырехугольник. Докажите, что все его стороны равны. | 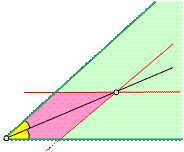
|
| 
|
| 4. Биссектриса угла прямоугольника разбивает его другую сторону на отрезки с длинами 5 и 7 см. так, как это показано на рисунке. Найдите этого площадь прямоугольника. | 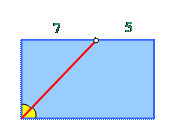
|
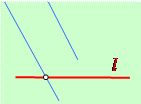
| 5. Докажите, что прямые АВ и CD на рисунке клетчатой бумаги параллельны. | 
|
| 6. Докажите, что отрезки АВ и СD на рисунке клетчатой бумаги делятся точкой пересечения пополам. | 
|
| 7. Противоположные стороны четырехугольника попарно равны. Докажите, что эти строны лежат на параллельных прямых. | 
|
| 
|
| 
|
| 
|
|