| Пример. Движение точки задано уравнениями | x =3 t, | y = -4 t 2+10,где x, | |||||||||||||||||||||||||
| y - | выражены | в сантиметрах, | а t - в | у, см | |||||||||||||||||||||||
| секундах. Определить ускорение точки. | |||||||||||||||||||||||||||
| 10 | М 0 | ||||||||||||||||||||||||||
| Исключив время t, получим уравнение | |||||||||||||||||||||||||||
| траектории: | y = - | x | +10. | Это | М | ||||||||||||||||||||||
| уравнение параболы (рис.8.8). | |||||||||||||||||||||||||||
| W | |||||||||||||||||||||||||||
| Находим | проекции | вектора | |||||||||||||||||||||||||
| ускорения на оси | |||||||||||||||||||||||||||
| О | 10 | х, | см | ||||||||||||||||||||||||
| Wx = x = 0, Wy = y = - 8 см/с2. | |||||||||||||||||||||||||||
| Тогда модуль | ускорения | W =8см/с2. | Рис. 8.8 | ||||||||||||||||||||||||
| Так | как проекция вектора | ускорения | на | ось x | равна | нулю, а | на | ось y | |||||||||||||||||||
| отрицательна, то W направлен вертикально вниз. |


Определение ускорения точки при естественном способе задания движения.
Прежде чем приступить к определению ускорения, познакомимся с некоторыми понятиями из дифференциальной геометрии.
Естественная система координат
Пусть имеется некоторая пространственная кривая (рис.8.9).
Возьмем на этой кривой две близкие точки M и M1. Проведем в этих точках касательные t и t 1. Через касательную t проведем плоскость, параллельную касательной t 1.
Если точку M1 приближать к точке M, плоскость, оставаясь параллельной касательной t 1, будет поворачиваться вокруг t. И в момент, когда точка M1
совпадает с точкой M, плоскость займет определенное положение I. Плоскость I называется соприкасающейся плоскостью кривой в точке M. Если кривая плоская, то вся кривая будет лежать в соприкасающейся плоскости.
| n | t1 | |||||
| II | I | |||||
| n 0 | М 1 | |||||
| t | ||||||
| в 0 | t | |||||
| М | ||||||
| III | ||||||
| III | ||||||
| в | Рис. 8.9 | |||||
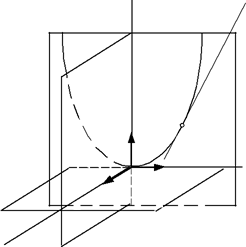
Проведем, затем, плоскость II через точку M, перпендикулярную касательной t. Эта
плоскость называется нормальной плоскостью. Линия пересечения соприка-сающейся плоскости и нормальной плоскости называется главной нормалью кривой в точке
M. Обозначим ее n. Нормаль, перпендикулярная главной нормали n и касательной t, называется бинормалью b.
Плоскость III, проведенная через b и t, является касательной плоскостью к кривой в
точке M.
Таким образом, мы получим систему осей
| естественной системой координат, где t 0 | , n 0 | , b 0 |
| Кривизна и радиус кривизны линии |
t, n, b, которая называется ее орты.
Если точка M движется по кривой, то эти оси также будут двигаться вместе с точкой, меняя свое направление в пространстве.
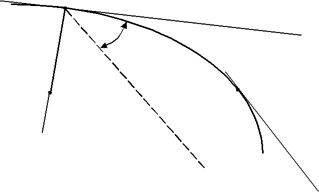
Введем еще одно понятие - понятие о кривизне и радиусе кривизны линии. Возьмем на кривой две близкие точки M и M1. (рис.8.10) и проведем
в этих точках касательные t и t 1. Угол между этими касательными называется углом смежности Dj.
| М | |||||
| r | Dj | Ds | |||
| С | М 1 | ||||
| n | |||||
| Рис. 8.10 Отношение угла смежности к длине дуги | D σ =MM1 называется средней | ||||
| кривизной линии Kср в точке M | |||||
| K cp= | j . | ||||
| Δσ | |||||
| Предел этого отношения при D s ® 0 называется кривизной линии в точке | |||||
| M: | |||||
| K = | lim K cp = | lim | j . | ||
| D s ®0 | D s ®0 Δσ | ||||
| Величина, обратная кривизне, называется радиусом кривизны линии в | |||||
| точке Mρ =1. | |||||
| K | |||||
| Если отложить ρ из точки M по главной нормали в сторону вогнутости | |||||
| линии, получим точку C, которая называется центром кривизны. | |||||
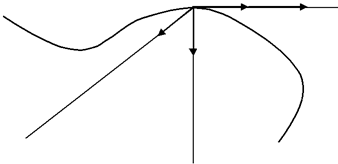
| Теперь можно приступить к определению ускорения точки. Пусть точка | |||||
| M движется по некоторой пространственной линии и имеет скорость V | |||||
| (рис.8.11). | М | t0 | V | ||
| n 0 | в 0 | ||||
| n | в | ||||
| Рис. 8.11 |



Подставим выражение вектора скорости (8.4) в формулу (8.5):
| d | dV | dt | ||||||||
| dV | ||||||||||
| W = | = | (Vt 0) = | t 0 | + V | . | |||||
| dt | dt | |||||||||
| dt | dt |
Очевидно, ускорение состоит из двух составляющих. Первая составляющая направлена вдоль касательной τ в сторону возрастания координаты S при
| dV | dS | |||
| dt | = | dt | = S | > 0 |
и в противоположную сторону при S <0.Чтобы определить модуль и
направление второго слагаемого, рассмотрим производную dt 0. Поскольку dt

t 0 является вектором с постоянным модулем, то его производная по времени представляет собой вектор, перпендикулярный t 0 и равный:
| dt | j | |||||
| = | lim | n 0 | , | |||
| dt | ||||||
| D t ®0 | D t |
где n 0 - единичный вектор главной нормали к траектории точки.
| Учитывая, что | ||||||||||||||||||||||||||||
| D j | D S | D j | dS | S | dt | S | V | |||||||||||||||||||||
| lim | = lim | lim | = | К = | , то | 0 | = | n | = | n. | ||||||||||||||||||
| D t | D t | D S | dt | r | dt | |||||||||||||||||||||||
| D t ®0 | D t ®0 | D S ®0 | r 0 | r 0 | ||||||||||||||||||||||||
| Таким образом, ускорение точки | ||||||||||||||||||||||||||||
| dV | V | |||||||||||||||||||||||||||
| W = | t 0 | + | n 0. | |||||||||||||||||||||||||
| r | ||||||||||||||||||||||||||||
| dt |
Итак, ускорение точки состоит из двух составляющих. Одна составляющая направлена по касательной к траектории и называется касательным ускорением. Его проекция на ось t
| W = | dV | = | d 2 S | . | |
| t | dt | dt 2 | |||
Вторая составляющая направлена по главной нормали в сторону вогнутости траектории, называется нормальным ускорением, а его модуль
Wn = Vr 2.

При естественном способе задания движения ускорение точки находим как векторную сумму двух взаимно перпендикулярных векторов касательного и нормального ускорений
W = Wt + Wn.

2 2
Модуль ускорения W = Wt + Wn.
- точка движется по прямой линии с переменной скоростью.
Ускорение точки
| dV | V | V | |||||||||
| W = | ¹0; W | n | = | = | =0; W = W; | ||||||
| t | dt | r | ¥ | t | |||||||
- точка движется по кривой с постоянной по величине скоростью. Ускорение точки
| dV | V | |||||
| W = | =0;W = | ¹0; W = W. | ||||
| t | dt | n | r | n | ||
В первом случае скорость точки изменялась только по величине, и ее ускорение равно касательному ускорению. Во втором случае скорость точки менялась по направлению, и ускорение равно нормальному ускорению.
Поэтому касательное ускорение характеризует изменение скорости по величине, а нормальное - по направлению.
| Пример. S = t 2-5 t +10м.Определить ускорение точки при t 1=2с и | t 2=3с | ||||||
| (рис.8.12). | |||||||
| Скорость точки V = | dS | = 2 t - 5. При t 1 | =2с V | = -1м/с При t 2 | =3с V | =1м/с. | |
| dt | |||||||
Следовательно, при t 1 =2с скорость точки направлена по касательной в сторону отрицательных значений криволинейных координат, а при t 2=3с - в сторону положительных значений координат.
| ¯ О + | V 1 | ¯ | О + | M | ||||||
| M 1 | V 2 | |||||||||
| S | W t | S | W t | |||||||
| W | Wn | |||||||||
| n | W 2 | |||||||||
| W | ||||||||||
| M 0 | ||||||||||
| при t 1 = 2 с | M 0 | при t 2 = 3 с | ||||||||
| Рис. 8.12 |

Величина касательного ускорения точки Wt = dVdt =2 м/с (постоянная, не

зависит от времени). Так как Wt > 0, вектор Wt направлен по касательной в сторону положительного направления оси t.
Нормальное ускорение:
| V 2 | V 2 | ||||||||||
| при | t 1=2с | W = | =0,2 м/с2; при | t 2=3с | W = | =0,2 м/с2. | |||||
| n | R | n | R | ||||||||
Так как составляющие равны по модулю, то ускорения точки в заданные моменты времени будут равны
W 1= W 2= 
 Wt 2+ Wn 2@2м/с.
Wt 2+ Wn 2@2м/с.

При t 1=2с направление касательного ускорения противоположно скорости, а при t 2=3с оба вектора имеют одинаковое направление. Следовательно, в момент t 1=2с движение точки замедленное, в момент t 2=3с – ускоренное.
Домашнее задание:
1. Прочитать конспект
2. Выписать основные формулы
3. Записать и разобраться в примере
4.