Способы задания множеств.

1) Множество можно задать, перечислив все его элементы.

2) Указывают характеристическое свойство его элементов.

Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.

Пример: А – множество двузначных чисел

Тогда характеристическим свойством множества А является свойство ” быть двузначным числом”

Характеристическое свойство можно (не всегда) задать в символической форме.

Например, множество А натуральных чисел, меньших 7, можно задать так:

А= {х½ хÎN, х< 7}, х – элемент множества А.

Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и В.

АÇВ={х½х Î А и х Î В}

АÇВ=Æ, если А и В не имеют общих элементов.

Пример: Рассмотрим множества А={а,b,c,d,e} и В={c,d,e}

AÇВ={c,d,e}=В. Тогда В является подмножеством множества А. Обозначают ВÌА

Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.

АÈВ={х½х ÎА или хÎВ}

Декартовым произведением множеств А и В называется множество всех пар, первое компанента которых принадлежит множеству А, а вторая компанента принадлежит множеству В.

Обозначают А´В.

А´В={(х;у)½хÎА Ù уÎВ}

Бинарным отношением на множестве Х называется всякое подмножество декартова произведения Х´Х.

Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой.

R рефлексивно на Х <=> хRх для " хÎХ.

Например: 1) отношение равенства

2) отношение “кратно” на N

3) отношение подобия треугольников

Отношение перпендикулярности не рефлексивно, т.к. отрезок не перпендикулярен сам себе.

Отношение R на множестве Х называется симметричным, если выполняются условия: из того, что элемент х находится в отношении R с элементом у, следует, что элемент у находится в отношении R с элементом Х

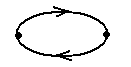На графе это

R симметрична на Х<=> (хRу<=>уRх)

Например, симметричными будут следующие отношения:

- отношение параллельности на множестве прямых.

- отношение подобия треугольников

Отношение R на множестве Х называется антисимметричным, если для различных элементов х и у из множества Х выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R c элементом х не находится

R антисимметрично на Х <=> (хRу Ù х¹<=> уRх)

На графе

 

Например, антисимметричными будут следующие отношения: длиннее, больше, больше на

Отношением R на множестве Х называется транзитивным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом Z, следует, что элемент х находится в отношении R с элементом Z.

R транзитивно на Х <=> (хRу Ù уRz<=>xRz)

Например, АВ=2см., АС=3см., и ДК=4см. Отношение “меньше”.

Если АВ<АС и АС<ДК, то АВ<ДК

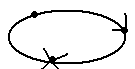
Граф транзитивного отношения с каждой парой стрелок, идущих от х к у и у к z, содержат стрелку, идущую от х к z.

Элементы теории графов. Основные понятия.

Такая структура, как граф (в качестве синонима используется также термин “сеть”), имеет самые различные применения в математике, информатике и в смежных прикладных областях, поэтому познакомимся с основными понятиями теории графов.

Граф G = (V, Е) задается парой конечных множеств V и Е. Элементы первого множества v1, v2,..., vM называются вершинами графа (при графическом представ­лении им соответствуют точки). Элементы второго множества e1, e2,..., eN называ­ют ребрами. Каждое ребро определяется парой вершин (при графическом представ­лении ребро соединяет две вершины графа). Если ребра графа определяются упоря­доченными парами вершин, то такой граф называют ориентированным (на чертеже при изображении ориентированного графа на каждом ребре ставят стрелку, указы­вающую его направление). Ориентированный граф с пятью вершинами и семью ребрами изображен на рисунке:

 

 

 

Если две вершины соединены двумя или более ребрами, то эти ребра называют параллельными (например, ребра е4 и е5). Если начало и конец ребра совпадают, то такое ребро называется петлей (например, ребро е7). Граф без петель и параллель­ных ребер называется простым.

Если ребро ek определяется вершинами vi и vj (будем обозначать этот факт следующим образом: ek = (vi, vj), то говорят, что ребро ek инцидентно вершинам vi и vj. Две вершины vi и vj называются смежными, если в графе существует ребро (vi, vj).

Последовательность вершин vi1, vi2,.... vik, таких, что каждая пара (yi,(j-1), vij) при 1 < j £ k определяет ребро, называется маршрутом в графе G. Вершины vi1 и vik называют концевыми вершинами маршрута, все остальные входящие в него вершины - внутренними.

Маршрут, в котором все определяемые им ребра различны, называют цепью. Цепь считают замкнутой, если ее концевые вершины совпадают. Замкнутая цепь, в которой все вершины (за исключением концевых) различны, называется циклом. Незамкнутая цепь, в которой все вершины различны, носит название путь. Если в ориентированном графе существует путь из vi в vj, то говорят, что вершина vj достижима из вершины vi.

Две вершины vi и vj называют связанными в графе G, если в нем существует путь, для которого эти вершины являются концевыми. Граф G называется связным, если каждые две вершины в нем являются связанными. На рис. 1.7 изображен простой неориентированный связный граф.

Последовательность вершин v1, v5, v 4, v 3, например, определяет путь, а после­довательность вершин v1, v5, v 4, v3, v1 - цикл. Деревом будем называть неориен­тированный связный граф без циклов. Лес - это любой граф без циклов. На рис. 1.8 показаны возможные деревья с пятью вершинами.

Анализ приведенных здесь понятий и определений показывает, что в качестве моделей графы удобно использовать в тех случаях, когда рассматривается система каких-либо объектов, между которыми существуют определенные связи, отноше­ния, когда изучается структура системы, возможности ее функционирования.

Представление графов

Важным вопросом, особенно для приложений теории графов, является определе­ние возможных способов представления графов. Самый простой способ - полное перечисление множеств V и Е. Однако, очевидно, что в этом случае выявление у графа различных характеристик и свойств будет крайне затруднительным. Граф можно представить в виде некоторого графического изображения и визуально определить некоторые свойства и характеристики заданного графа. Однако, при наличии в графе большого числа ребер и вершин этот способ также мало пригоден. Рассматривая различные возможные способы представления графов, мы должны иметь в виду потребность ввода соответствующей информации в компьютер. В этой связи ввод информации в числовом виде предпочтителен, хотя современные техниче­ские средства допускают ввод и графической информации (таблиц, текста, графиков, рисунков и т.д.), после чего может производиться обработка такой информации.

Матрица смежности. Если вершины графа G помечены метками v1, v2,..., vn, то элементы матрицы смежности A(G) размера V´V определяются следующим обра­зом: A(i,j} = 1, если vi смежна с vj; A(i,j) = 0 в противном случае (рис. 1.9, а).

Матрица инцидентности. Если вершины графа G помечены метками v1, v2,..., vm, а ребра - метками е1, е2,..., еп, то элементы матрицы инцидентности I(G) размера М х N определяются правилом: B(i,j) = 1, если vi инцидентна ej;

B(i,j) = 0 в против­ном случае (см. рис. 1.9, б).

а

b

с

d

e

f

g

A(G): 3

I(G): 3

_

 

Рис. 1.9, а. Матрица смежности Рис. 1.9, б. Матрица инцидентности

Для ориентированного графа G, имеющего N вершин, можно рассмотреть матрицу достижимости C(G) размера N х N, элементы которой определяются так: C(I, J) = 1, если вершина vj достижима из vi; C(I, J) = 0 в противном случае. Ниже приведен пример ориентированного графа.

 

 

Перечень литературы

Основная:
1 Баврин И.И. Высшая математика: Учеб. для студ. естественнонаучных специальностей педагогических вузов. -М.: Издательский центр "Академия"; Высшая школа, 2000.-616с.
2 Пехлецкий И.Д. Математика: Учебник. -М.: Мастерство, 2001.-304с.
	Дополнительная:
	Богомолов Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учеб. заведений - 5-ое изд., стер. - М.: Высш. шк., 2002.-495 с.
	Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб. пособие.- 2-ое изд., перераб. и доп.-М.: Наука, 1990-576с.
	Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. ч. I: Учебное пособие для втузов.- 5-е изд. - М.: Высш. шк., 1996.-304с.
	Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. ч. II: Учебное пособие для втузов.- 5-е изд. - М.: Высш. шк., 1996.-416с.
	Калинина В.Н., Панкин В.Ф. Математическая статистика: Учеб. для студ. сред. спец. учеб. заведений.- 3-е изд.-М.:Высш. шк., 2001.-336с.
	Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах: Учеб. Пособие.- М.: Высш.шк., 2001.-376 с.
	Стойлова Л.П. Математика: Учебник для студ. высш. пед. учеб. заведений. - М.: Издательский центр "Академия", 1999. - 424с.