Почему так красива, правильна форма кристалла? Грани его блестящие и ровные и выглядят так, как будто бы над кристаллом поработал искусный шлифовальщик. Отдельные части кристалла повторяют друг друга, образуя красивую симметричную фигуру.
Эта исключительная правильность кристаллов была знакома уже людям древности. Но представления древних учёных о кристаллах мало отличались от сказок и легенд, сочинённых поэтами, воображение которых было пленено красотой кристаллов. Верили, что хрусталь образуется изо льда, а алмаз – из хрусталя. Кристаллы наделялись множеством таинственных свойств: исцелять от болезней, предохранять от яда, влиять на судьбу человека…
Лишь в XVII–XVIII веках появились первые научные взгляды на природу кристаллов. Представление о них даёт рисунок 11, заимствованный из книги XVIII века. По мнению её автора, кристалл построен из мельчайших «кирпичиков», плотно приложенных друг к другу. Эта мысль довольно естественна. Разобьём сильным ударом кристалл кальцита (углекислый кальций). Он разлетится на кусочки разной величины. Рассматривая их внимательно, мы обнаружим, что эти куски имеют правильную форму, вполне подобную форме большого кристалла – их родителя. Наверно, рассуждал учёный, и дальнейшее дробление кристалла будет происходить таким же образом, пока мы не дойдём до мельчайшего, невидимого глазом кирпичика, представляющего кристалл данного вещества. Эти кирпичики так малы, что построенные из них ступенчатые «лестницы» – грани кристалла кажутся нам безукоризненно гладкими. Ну, а дальше, что же представляет собой этот «последний» кирпич? На такой вопрос учёный того времени ответить не мог.
Рис. 11. Справа кристалл, слева его строение, по мысли учёных XVIII века.
Эта «кирпичная» теория строения кристалла принесла науке большую пользу. Она объяснила происхождение прямых рёбер и граней кристалла: при росте кристалла одни кирпичики подстраиваются к другим, и грань растёт, как стена дома, выкладываемая руками невидимого каменщика. С точки зрения «кирпичной» теории понятно, что правильная форма кристалла есть проявление его внутренних свойств. Из большого кристалла, скажем каменной соли, можно выточить шар. Грани и рёбра кристалла исчезли, но на самом деле они существуют, хотя и в скрытом виде. Начнём медленно растворять шар из каменной соли. Мы увидим, как по мере растворения из шара образуется… куб, то есть та форма, которая свойственна кристаллу данного вещества (см. стр. 54).
Поговорим об обоях
Теперь мы хотим дать читателю современные представления о природе кристалла. Для этого сначала нам придётся поговорить… об обоях. Посмотрите на рисунок 12. На нём изображена девочка, играющая в мяч. И не одна девочка, а много совершенно одинаковых фигурок. Найдём на этом рисунке обоев тот наименьший кусок, который надо нарисовать художнику, иначе говоря, тот кусок, простым перекладыванием которого можно составить все обои. Чтобы выделить такой кусок, проведём из любой точки рисунка, например из центра мячика, две линии, соединяющие выбранный мячик с двумя соседними. На этих линиях можно построить, как это видно на нашем рисунке, параллелограмм. Совершенно ясно, что перекладываниям этого кусочка в направлении основных исходных линий мы можем составить весь рисунок обоев.
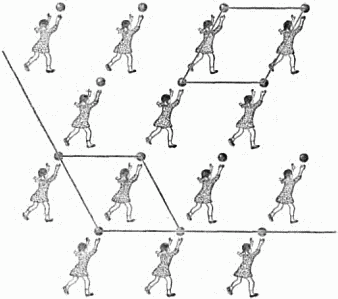
Рис. 12. Рисунок этих простеньких обоев помогает нам понять решетчатое строение кристаллов.
Этот наименьший кусок может быть выбран по-разному: из рисунка сразу видно, что можно выбрать несколько разных параллелограммов, каждый из которых содержит одну фигурку. Подчеркнём, что для нас в данном случае безразлично, будет ли эта фигурка внутри выделенного куска целой или разделённой на части линиями, ограничивающими этот кусок.
Было бы неверным полагать, что, изготовив повторяющуюся на обоях фигурку, художник может считать свою задачу оконченной. Это было бы так лишь в том случае, если составление обоев можно было бы провести единственным способом – прикладыванием к данному кусочку, содержащему одну фигурку, другого такого же, параллельно сдвинутого. Однако кроме этого простейшего способа есть ещё шестнадцать способов заполнения обоев закономерно повторяющимся рисунком, то есть, всего существует 17 типов взаимных расположений фигурок на плоскости. Они показаны на рисунке 13[3].

Рис. 13. 17 типов симметрии плоского узора; элементарные ячейки выделены.
В качестве повторяющегося рисунка здесь выбрана более простая, но, так же как и на рисунке 12, лишённая собственной симметрии фигурка. Однако составленные из неё узоры симметричны, и их различие определяется различием симметрии расположения фигурок.
Мы видим, что, например, в первых трёх случаях рисунок не обладает зеркальной плоскостью симметрии – нельзя поставить вертикальное зеркало так, чтобы одна часть рисунка была «отражением» другой части. Напротив, в случаях 4 и 5 имеются плоскости симметрии. В случаях 8 и 9 можно «установить» два взаимно перпендикулярных зеркала. В случае 10 имеются оси 4-го порядка, перпендикулярные чертежу, в случае 11 – оси 3-го порядка. В случаях 13 и 15 имеются оси 6-го порядка и т.д.
Плоскости и оси симметрии наших рисунков выступают не по одиночке, а параллельными семействами. Если мы нашли одну точку, через которую можно провести ось (или плоскость) симметрии, то найдём быстро и соседнюю, и далее на таком же расстоянии третью и четвёртую и т.д. точки, через которые проходят такие же оси (или плоскости) симметрии.
Выберем теперь на этих узорах такой наименьший кусок, перемещая который параллельно самому себе на расстояния, равные длинам его сторон, мы сможем воспроизвести всю картину обоев. Мы столкнёмся при этом с несколькими интересными обстоятельствами.
Во-первых, этот наименьший кусок, или, как его принято называть, элементарная ячейка может оказаться параллелограммом (например, случай 1 на рисунке 13), прямоугольником (случаи 3, 4 и др.), ромбом с углом 60° или же квадратом.
Во-вторых, на элементарную ячейку в разных случаях приходится различное число фигурок. Это число равно 1 для случая 1, 4 для случая 8, 6 для случая 17 и т.д.
Принято выбирать элементарные ячейки так, чтобы они были наименьшими, но отражали бы симметрию, присущую узору в целом. Так, в случае 9 можно выбрать прямоугольную ячейку, на которую приходится 8 фигурок, и вдвое меньшую косоугольную. Рисунок указывает на высокую симметрию взаимного расположения фигурок – наличие взаимно перпендикулярных плоскостей симметрии. Косоугольная элементарная ячейка делала бы не очевидной эту высокую симметрию. Поэтому здесь и в других подобных случаях в качестве элементарной ячейки выбирается прямоугольник.
Однако некоторая свобода выбора в расположении элементарной ячейки всегда имеется. Так, совершенно безразлично, поместим ли мы углы ячейки в местах «головок» или «хвостиков» фигурок или же где-либо на белом поле между ними. В случаях 14 или 15 выбор ячейки несколько лучше подчёркивает симметрию обоев, чем, скажем, в случае 8, но сути дела это не меняет, и мы можем, если желаем, произвольно переместить углы ячейки в случае 8, оставляя, конечно, размеры ячейки теми же и стороны её параллельными самим себе.
Способы заполнения элементарной ячейки отдельными фигурками во всех случаях различны. Этим прежде всего и отличаются друг от друга изображённые 17 случаев. Таким образом, художник, выполнивший повторяющийся рисунок обоев, должен указать, кроме того, каким из 17 способов надо построить обои из его рисунка. Например, для случая 8 надо выполненный рисунок расположить в заштрихованной части (одной четверти) элементарной ячейки и отразить его в двух «зеркалах» (рис. 14).
17 типов симметрии плоского узора не исчерпывают, конечно, всего разнообразия узоров, составляемых из одной и той же фигурки: художник должен указать ещё одно обстоятельство, – как расположить фигурку по отношению к граничным линиям ячейки. На рисунке 14 показаны два узора обоев с той же исходной фигуркой, но различно расположенной по отношению к зеркалам. Оба эти узора относятся к случаю 8.

Рис. 14. Два разных расположения фигурок при одинаковом типе симметрии узора.
Мы не станем приводить правила построения обоев во всех остальных случаях.
Какое же отношение имеют обои к кристаллу?
Каждое тело, в том числе и кристалл, состоит из атомов. Простые вещества состоят из одинаковых атомов, сложные – из атомов двух или нескольких сортов. Предположим, что мы могли бы в сверхмощный микроскоп рассмотреть поверхность кристалла поваренной соли и увидеть центры атомов. Рисунок 15 показывает, что атомы расположены вдоль грани кристалла, как узор обоев.

Рис. 15. Схема расположения атомов натрия (I) и хлора (II) на грани куба кристалла каменной соли.
Теперь мы готовы к тому, чтобы понять, как построен кристалл. Кристалл представляет собой «пространственные обои». Пространственные, то есть объёмные, а не плоские элементарные ячейки – это «кирпичи», прикладыванием которых друг к другу в пространстве строится кристалл.
Сколько же способов построения «пространственных обоев» из элементарных кусков? Эта сложная математическая задача была также решена Е.С. Фёдоровым. Он доказал, что должны существовать 230 способов построения кристалла или, как сейчас говорим, 230 фёдоровских групп. Открытие Е.С. Фёдорова принадлежит к величайшим достижениям русской науки. Начатые примерно через 20 лет после вывода Фёдорова опытные проверки его теории – они стали возможными лишь после открытия рентгеновского структурного анализа – привели к блестящему её подтверждению. Не было найдено ни одного кристалла, который не принадлежал бы к той или иной фёдоровской группе.
Все современные данные о внутреннем строении кристаллов получены при помощи рентгеновского структурного анализа, открытого в 1912 году.
Маленький, размером 0,5–1 мм, кристаллик ставится на пути узкого рентгеновского луча. За кристаллом помещается фотопластинка. Наряду с прошедшим сквозь кристалл лучом возникает ряд отклонённых лучей. Мы не будем здесь останавливаться на причине их возникновения. Явление это носит название дифракции.
Проявленная фотопластинка обнаруживает много пятен, по расположению и интенсивности которых можно судить о структуре кристалла. Примерный вид такого снимка – рентгенограммы топаза – приведён на рисунке 16 (в действительности пятна обычно несколько размыты и различаются не столько по величине, сколько по яркости); справа внизу указаны размеры кристаллика. Расшифровка рентгенограмм представляет собой сложную задачу.

Рис. 16. Рентгенограмма кристалла топаза.
Огромное значение для развития рентгеноструктурного анализа имели труды известного русского кристаллографа Г.В. Вульфа. За время, протекшее после открытия рентгеноструктурного анализа, этим методом было изучено строение многих тысяч кристаллов.
Невидимые решётки
Существуют простые кристаллы, построенные из атомов одного сорта. Например, алмаз – это чистый углерод. Кристаллы поваренной соли состоят из ионов (электрически заряженных атомов) двух сортов – натрия и хлора. Более сложные кристаллы могут быть построены из молекул, которые в свою очередь состоят из атомов многих сортов.
Однако в кристалле всегда можно выделить наименьшую повторяющуюся группу атомов (в простейшем случае это будет один атом), что соответствует повторяющейся на плоских обоях рисунка 13 одной фигурке.
Как и на рисунке обоев, в кристалле всегда можно найти элементарную ячейку, – то есть такой параллелепипед (для плоских обоев это был прямой или косоугольный параллелограмм), последовательным перемещением которого параллельно самому себе на расстояния, равные его рёбрам, можно воспроизвести весь кристалл.
Повторяющиеся группы атомов (или отдельные атомы) укладываются друг по отношению к другу внутри элементарной ячейки кристалла вполне определённым образом – одним из 230 способов Фёдорова.
Вершины ячейки кристаллографы называют узлами. Обычно их удобнее всего размещать в центрах атомов кристалла. При этом, конечно, не все атомы попадают в вершины ячеек. В самых сложных кристаллах элементарная ячейка будет косоугольным параллелепипедом. В более симметричных кристаллах ячейка имеет форму, например, прямоугольного параллелепипеда. Наиболее симметричные кристаллы – кубические, их ячейка имеет форму куба.
Если изобразить в пространстве строение кристалла, отмечая только узлы и соединяющие их линии, то возникнет своего рода «скелет» кристалла. Этот скелет, сделанный из проволоки и узлов–шариков, показан на рисунке 17; такое изображение кристалла называется кристаллической пространственной решёткой. Изучим сначала «скелет» кристалла, а затем уже будем облекать его плотью.

Рис. 17. Модель кристаллической решётки.
Основная особенность кристаллической структуры заключается в её повторяемости через строго одинаковые расстояния. Предположим, что мы сделали прогулку вдоль одной из проволочек рисунка 17. Выйдя из узла и продвигаясь вдоль проволоки, мы попадали бы всё в новые «местности». Но наши новые впечатления продолжались бы лишь до следующего узла. Начиная же от него, мы увидели бы полное повторение «пейзажа», уже знакомого нам по путешествию от первого до второго узла.
Двигаясь в разных направлениях внутри кристалла, мы наблюдали бы разные картины, но во всех случаях, пройдя некоторое расстояние, мы попадали бы в места, неотличимые от уже пройденных, и это повторялось бы всё время через равные промежутки.
Размеры ячейки могут быть весьма различными. Наименьшие расстояния между соседними узлами встречаются у простейших кристаллов, построенных из атомов одного сорта, наибольшие – у сложных кристаллов белка. Расстояния колеблются от 2–3 до нескольких сот ангстремов (стомиллионных долей сантиметра), в последнем случае соответствуя уже размерам, видимым в электронный микроскоп.
Кристаллические решётки очень разнообразны. Однако свойства, общие для всех кристаллов, безупречно объясняются решетчатым строением кристаллов. Прежде всего, нетрудно понять, что идеально плоские грани – это плоскости, проходящие через узлы, в которых сидят атомы. Но узловых плоскостей можно провести сколько угодно по самым различным направлениям. Какие же из этих узловых плоскостей ограничивают выросший кристалл? Обратим внимание прежде всего на следующее обстоятельство: разные узловые плоскости и линии заполнены узлами не одинаково плотно. Опыт показывает, что кристалл огранён плоскостями, которые гуще всего усеяны узлами, плоскости же пересекаются по рёбрам, в свою очередь, наиболее густо заселённым узлами.
Рисунок 18 даёт вид кристаллической решётки перпендикулярно к её грани; проведены следы некоторых узловых плоскостей, перпендикулярных чертежу. Из сказанного ясно, что у кристалла могут развиться грани, параллельные узловым плоскостям I, и не будет граней, параллельных редко усеянным узлами плоскостям II.

Рис. 18. Схема расположения некоторых узловых плоскостей в кристаллической решётке; плоскости I могут служить внешними гранями, II – нет.
Внешняя симметрия кристалла также определяется типом его решётки. Наиболее симметричными бывают кристаллы с кубической элементарной ячейкой. К высокосимметричным относятся также кристаллы с ячейкой в виде прямой призмы, у которой в основании лежит квадрат или ромб с углом 60°.
Облечём теперь скелеты-решётки плотью, перейдём к рассмотрению упаковки частиц в кристаллах.