Математика - 9 класс - Подготовка к ОГЭ
Множества чисел
N - натуральные числа  Z - целые числа
Z - целые числа  Q - рациональные числа
Q - рациональные числа  (обыкновенные дроби, конечные или бесконечные периодические десятичные дроби) пр:
(обыкновенные дроби, конечные или бесконечные периодические десятичные дроби) пр:  I - иррациональные числа (не рациональные, бесконечные непериодические десятичные дроби)
пр:
I - иррациональные числа (не рациональные, бесконечные непериодические десятичные дроби)
пр:  R - действительные (вещественные) числа (все точки числовой оси, от
R - действительные (вещественные) числа (все точки числовой оси, от 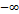 до до  )
С - комплексные (мнимые) числа ( )
С - комплексные (мнимые) числа ( 
| 

|
| № 1
| Приведите примеры:
натуральных чисел ________________________________
целых чисел ________________________________
рациональных чисел ________________________________
иррациональных чисел ________________________________
действительных чисел ________________________________
|
| Действия с натуральными числами
| 
| умножение
 степень
степень
 пр:
пр: 
|
| пр:
| 
| 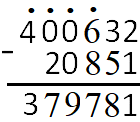
| 
|
| | | | | | |
| Порядок действий (слева направо)
1) скобки 2) степень 3) умножение, деление 4) сложение, вычитание
|
| № 3
| Определите порядок действий и вычислите (по действиям):


|
Распределительный закон для умножения и деления больших чисел (для устного счета)
пр: 



|
| № 4
| Решите с помощью распределительного закона:
|
| разложение на простые множители
позволяет увидеть «состав» числа - на что оно делится
простое число - делятся только на 1 и «само себя»
взаимно простые числа - не имеют общих делителей (кроме 1)
| пр: разложим 168 на простые множители
делим только на простые числа, начиная с 2
 168 = 2 · 2 · 2 · 3 · 7 168 = 2 · 2 · 2 · 3 · 7
| 
|
| № 5
| Разложите число на простые множители:

|
| Основное свойство дроби: числитель и знаменатель можно умножить (или разделить) на одно число
|
|
пр:  или или   или или 
|
| при сокращении дробей нужно пользоваться признаками делимости, сокращать поэтапно
| пр: 
| число делится на 3 если сумма его цифр делится на 3
|
| | | | |
| № 6
| Сократите дробь:
а)  б) б)  Что получится, если эту дробь «сократить» на 5:
Что получится, если эту дробь «сократить» на 5: 
|
Cравнение дробей
если знаменатели одинаковые, то чем больше числитель, тем больше дробь  если числители одинаковые, то чем больше знаменатель, тем меньше дробь
если числители одинаковые, то чем больше знаменатель, тем меньше дробь  если дроби имеют разные знаменатели (и числители), то их нужно сначала привести к общему знаменателю (или числителю) умножением на «дополнительный множитель»
если дроби имеют разные знаменатели (и числители), то их нужно сначала привести к общему знаменателю (или числителю) умножением на «дополнительный множитель»
|
всегда можно каждую из дробей домножить на знаменатель другой
пр: сравнить дроби 

| иногда достаточно домножить только одну из дробей
пр: сравнить дроби 

| иногда нужно домножать обе дроби, подобрав наименьшие дополнительные множители
пр: сравнить дроби 

|
в сложных случаях, чтобы подобрать наименьшие дополнительные множители, можно разложить знаменатели на множители (чтобы увидеть «общие» и «дополнительные»):
пр: сравнить дроби 
| заметим, что
 5 и 7 - доп. множители
(должны быть взаимно простыми)
5 и 7 - доп. множители
(должны быть взаимно простыми)
| 
|
|
| Умножение дробей
| 
| Деление дробей
| 
|
пр:  не забывайте сокращать перед умножением
не забывайте сокращать перед умножением
| пр:  сокращать можно только после перехода к умножению
сокращать можно только после перехода к умножению
|
целое число можно записать дробью со знаменателем 1
пр:  пр: пр:  пр:
пр: 
| полезно запомнить правила:
 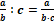 
|
| | | | | |
| № 8
| Вычислите:
а)  б) б)  в) в)  г)
г)  д) д) 
|
Сложение и вычитание дробей  (если дроби имеют общий знаменатель)
если дроби имеют разные знаменатели, то их нужно сначала привести к общему знаменателю
(если дроби имеют общий знаменатель)
если дроби имеют разные знаменатели, то их нужно сначала привести к общему знаменателю
| пр:  пр:
пр: 
|
Cмешанная дробь - запись числа в виде целой и дробной части
пр: перевести смешанную дробь в простую
 полезно запомнить правило: к числителю прибавляем целую часть, умноженную на знаменатель
полезно запомнить правило: к числителю прибавляем целую часть, умноженную на знаменатель
| 
| пр: перевести простую дробь в смешанную (выделить целую часть)
|
| № 11
| а) Запишите в виде простой дроби:  б) Запишите в виде смешанной дроби:
б) Запишите в виде смешанной дроби: 
|
| № 12
| Вычислите (по действиям): 

|
перевод обыкновенной дроби в десятичную
привести знаменатель к «круглому» числу пр:  или разделить числитель на знаменатель столбиком, при этом может получиться бесконечная периодическая дробь
или разделить числитель на знаменатель столбиком, при этом может получиться бесконечная периодическая дробь
| перевод десятичной дроби в обыкновенную
знаменатель определяется количеством цифр после запятой
пр: 
|
| № 15
| Вычислите:
а)  б) б)  в) в) 
 г)
г)  д) д)  е) е) 

|
дробное выражение с десятичными дробями
пр: 
| «многоэтажные» дроби
пр: 
| такие дроби лучше не использовать - вместо дробной черты пользоваться знаком «:»
|
| № 16
| Вычислите:
а)  б) б)  в)
в) 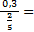 г) г) 
|
запись действий с отрицательными числами
пр:  расставляем порядок действий:
расставляем порядок действий:
 остались знаки «-», не занятые под действия, они относятся к отрицательным числам
остались знаки «-», не занятые под действия, они относятся к отрицательным числам
| при выполнении действий, сначала записываем знак результата, потом вычисляем его абсолютную величину (действие записывается «в строчку», а ниже «столбик» с положительными числами)
1) 


|
| № 19
| Вычислите (по действиям): 
 Вычислите (по действиям):
Вычислите (по действиям): 

|
| № 20
| Вычислите:

 действия с числами в стандартном виде
действия с числами в стандартном виде
 «разложение по разрядным слагаемым»
«разложение по разрядным слагаемым»
|
 Z - целые числа
Z - целые числа  Q - рациональные числа
Q - рациональные числа  (обыкновенные дроби, конечные или бесконечные периодические десятичные дроби) пр:
(обыкновенные дроби, конечные или бесконечные периодические десятичные дроби) пр:  I - иррациональные числа (не рациональные, бесконечные непериодические десятичные дроби)
пр:
I - иррациональные числа (не рациональные, бесконечные непериодические десятичные дроби)
пр:  R - действительные (вещественные) числа (все точки числовой оси, от
R - действительные (вещественные) числа (все точки числовой оси, от 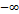 до
до  )
С - комплексные (мнимые) числа (
)
С - комплексные (мнимые) числа ( 



 степень
степень
 пр:
пр: 

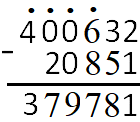

 0 б)
0 б) 







 168 = 2 · 2 · 2 · 3 · 7
168 = 2 · 2 · 2 · 3 · 7


 или
или 
 или
или 

 б)
б)  Что получится, если эту дробь «сократить» на 5:
Что получится, если эту дробь «сократить» на 5: 
 если числители одинаковые, то чем больше знаменатель, тем меньше дробь
если числители одинаковые, то чем больше знаменатель, тем меньше дробь  если дроби имеют разные знаменатели (и числители), то их нужно сначала привести к общему знаменателю (или числителю) умножением на «дополнительный множитель»
если дроби имеют разные знаменатели (и числители), то их нужно сначала привести к общему знаменателю (или числителю) умножением на «дополнительный множитель»








 не забывайте сокращать перед умножением
не забывайте сокращать перед умножением
 сокращать можно только после перехода к умножению
сокращать можно только после перехода к умножению
 пр:
пр:  пр:
пр: 

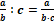

 б)
б)  в)
в)  г)
г)  д)
д) 
 (если дроби имеют общий знаменатель)
если дроби имеют разные знаменатели, то их нужно сначала привести к общему знаменателю
(если дроби имеют общий знаменатель)
если дроби имеют разные знаменатели, то их нужно сначала привести к общему знаменателю
 пр:
пр: 

 б)
б) 
 в)
в) 

 б) Запишите в виде смешанной дроби:
б) Запишите в виде смешанной дроби: 


 или разделить числитель на знаменатель столбиком, при этом может получиться бесконечная периодическая дробь
или разделить числитель на знаменатель столбиком, при этом может получиться бесконечная периодическая дробь





 (прочитайте эти дроби)
какие обыкновенные дроби можно записать в виде конечной десятичной дроби?
а) Запишите в виде десятичной дроби:
(прочитайте эти дроби)
какие обыкновенные дроби можно записать в виде конечной десятичной дроби?
а) Запишите в виде десятичной дроби:  б) Запишите в виде обыкновенной дроби:
б) Запишите в виде обыкновенной дроби:  в) Округлите десятичную дробь 3236,529
в) Округлите десятичную дробь 3236,529


 б) Запишите какое-нибудь число, которое находится между числами:
1,02 и 1,03:
б) Запишите какое-нибудь число, которое находится между числами:
1,02 и 1,03:  и
и  :
:
 б)
б)  в)
в) 
 г)
г)  д)
д)  е)
е) 



 б)
б)  в)
в) 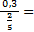 г)
г) 
 противоположные числа расположены по разные стороны от 0, но имеют одинаковую «абсолютную величину» - модуль: пр:
противоположные числа расположены по разные стороны от 0, но имеют одинаковую «абсолютную величину» - модуль: пр:  противоположные числа «по модулю» равны
если к одному числу относятся два знака:
противоположные числа «по модулю» равны
если к одному числу относятся два знака:

 пр:
пр: 
 пр:
пр: 
 пр:
пр: 
 (взяв за единичный отрезок 5 клеток)
(взяв за единичный отрезок 5 клеток)
 Сравните:
Сравните: 
 расставляем порядок действий:
расставляем порядок действий:
 остались знаки «-», не занятые под действия, они относятся к отрицательным числам
остались знаки «-», не занятые под действия, они относятся к отрицательным числам




 Вычислите (по действиям):
Вычислите (по действиям): 

 пр:
пр: 
 пр:
пр: 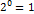

 cтандартный вид числа
cтандартный вид числа
 (мантисса)
(мантисса)  (порядок)
пр:
(порядок)
пр: 
 пр:
пр: 


 действия с числами в стандартном виде
действия с числами в стандартном виде
 «разложение по разрядным слагаемым»
«разложение по разрядным слагаемым»








 5 и 7 - доп. множители
(должны быть взаимно простыми)
5 и 7 - доп. множители
(должны быть взаимно простыми)





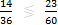 дополнительные множители - взаимно простые числа
дополнительные множители - взаимно простые числа
 к общему числителю
к общему числителю




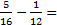

 полезно запомнить правило: к числителю прибавляем целую часть, умноженную на знаменатель
полезно запомнить правило: к числителю прибавляем целую часть, умноженную на знаменатель





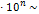 сдвинуть запятую на n позиций вправо
сдвинуть запятую на n позиций вправо сдвинуть запятую на n позиций влево
сдвинуть запятую на n позиций влево


































