Расчетные задания
1.Вычислить двойной интеграл  по прямоугольной области
по прямоугольной области 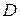 . Нарисовать область интегрирования.
. Нарисовать область интегрирования.
1. 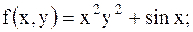
| 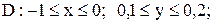
|
2. 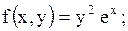
| 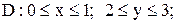
|
3. 
| 
|
4. 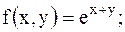
| 
|
5. 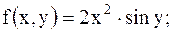
| 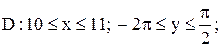
|
6. 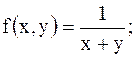
| 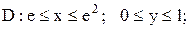
|
7. 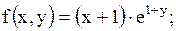
| 
|
8. 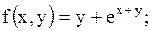
| 
|
9. 
| 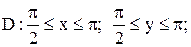
|
10. 
| 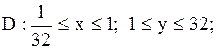
|
11. 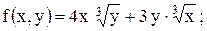
| 
|
12. 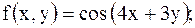
| 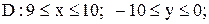
|
13. 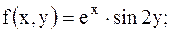
| 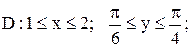
|
14. 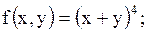
| 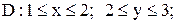
|
15. 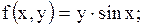
| 
|
16. 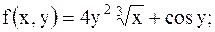
| 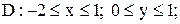
|
17. 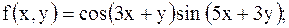
| 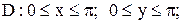
|
18. 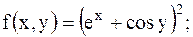
| 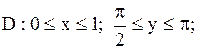
|
19. 
| 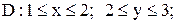
|
20. 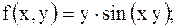
| 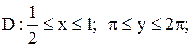
|
21. 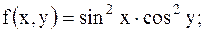
| 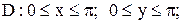
|
22. 
| 
|
23. 
| 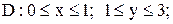
|
24. 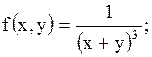
| 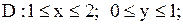
|
25. 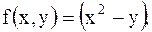
| 
|
26. 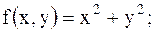
| 
|
27. 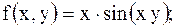
| 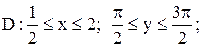
|
28. 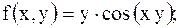
| 
|
29. 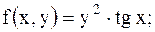
| 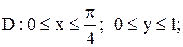
|
30. 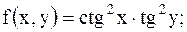
| 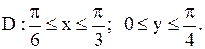
|
Изменить порядок интегрирования. Нарисовать область интегрирования
1. 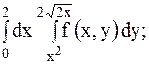
| 16. 
|
2. 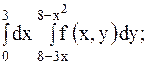
| 17. 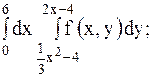
|
3. 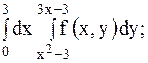
| 18. 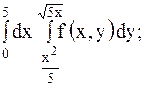
|
4. 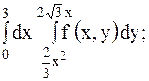
| 19. 
|
5. 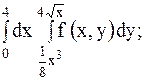
| 20. 
|
6. 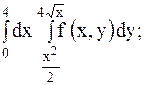
| 21. 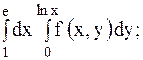
|
7. 
| 22. 
|
8. 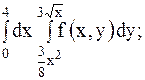
| 23. 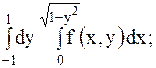
|
9. 
| 24. 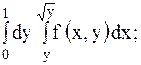
|
10. 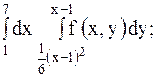
| 25. 
|
11. 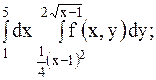
| 26. 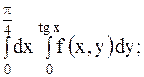
|
12. 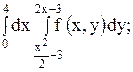
| 27. 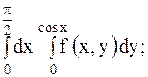
|
13. 
| 28. 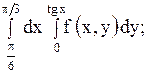
|
14. 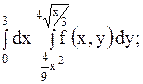
| 29. 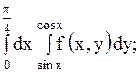
|
15. 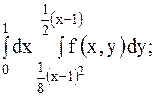
| 30. 
|
Вычислить двойной интеграл и нарисовать область интегрирования
1. 
| 
|
2. 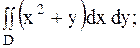
| 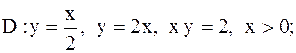
|
3. 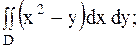
| 
|
4. 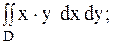
| 
|
5. 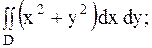
| 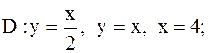
|
6. 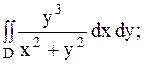
| 
|
7. 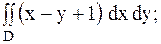
| 
|
8. 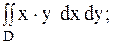
| 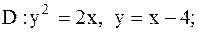
|
9. 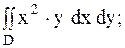
| 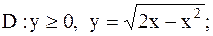
|
10. 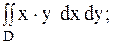
| 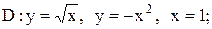
|
11. 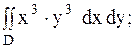
| 
|
12. 
| 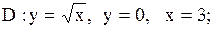
|
13. 
| 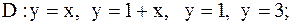
|
14. 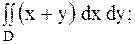
| 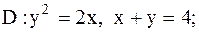
|
15. 
| 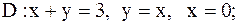
|
16. 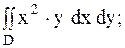
| 
|
17. 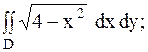
| 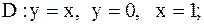
|
18. 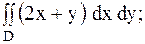
| 
|
19. 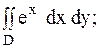
| 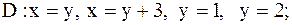
|
20. 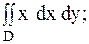
| 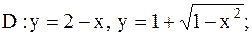
|
21. 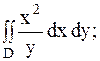
| 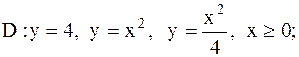
|
22. 
| 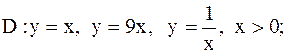
|
23. 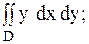
| 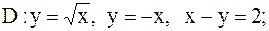
|
24. 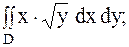
| 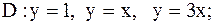
|
25. 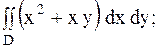
| 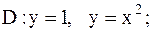
|
26. 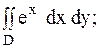
| 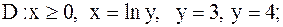
|
27. 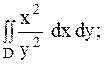
| 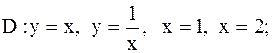
|
28. 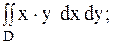
| 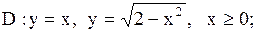
|
29. 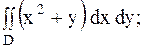
| 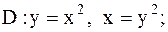
|
30. 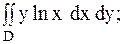
| 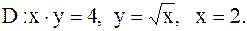
|
4. Вычислить двойной интеграл, применяя переход в полярную систему координат  . Нарисовать область интегрирования.
. Нарисовать область интегрирования.
1. 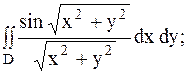
| 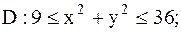
|
2. 
| 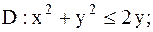
|
3. 
| 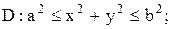
|
4. 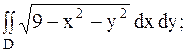
| 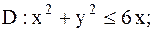
|
5. 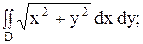
| 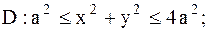
|
6. 
| 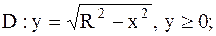
|
7. 
| 
|
8. 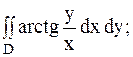
| 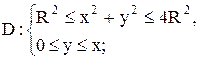
|
9. 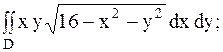
| 
|
10. 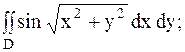
| 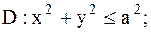
|
11. 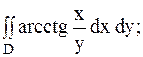
| 
|
12. 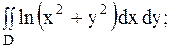
| 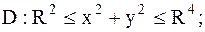
|
13. 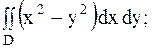
| 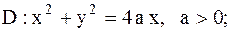
|
14. 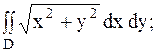
| 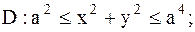
|
15. 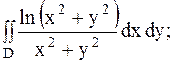
| 
|
16. 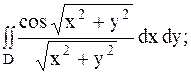
| 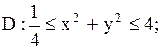
|
17. 
| 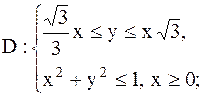
|
18. 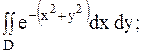
| 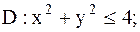
|
19. 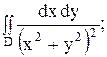
| 
|
20. 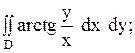
| 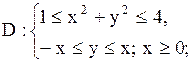
|
21. 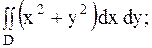
| 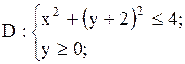 указание: полагаем:
указание: полагаем: 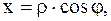
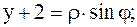
|
22. 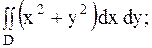
| 
|
23. 
| 
|
24. 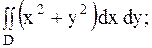
| 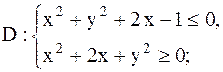
|
Указание: полагаем
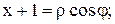 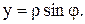
| |
25. 
| 
|
26. 
| 
|
27. 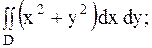
| 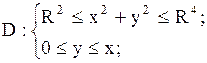
|
28. 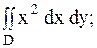
| 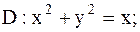
|
29. 
| 
|
30. 
| 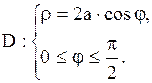
|
5. Найти площадь фигуры, ограниченной данными линиями с помощью двойного интеграла. (Перейти в полярную систему координат, сделать рисунок в полярной системе координат).
1. 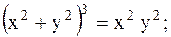
| 16. 
|
2. 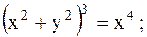
| 17. 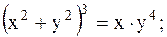
|
3. 
| 18. 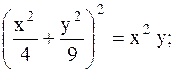 Указание:
Указание: 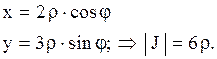
|
4. 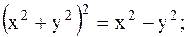
| 19. 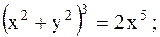
|
5. 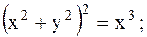
| 20. 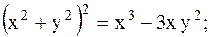
|
6. 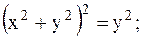
| 21. 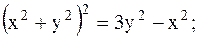
|
7. 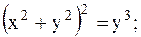
| 22. 
|
8. 
| 23. 
|
9. 
| 24. 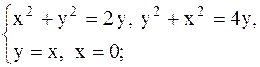
|
10. 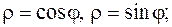
| 25. 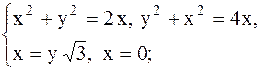
|
11. 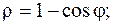
| 26. 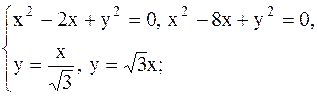
|
12. 
| 27. 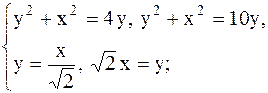
|
13. 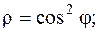
| 28. 
|
14. 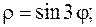
| 29. 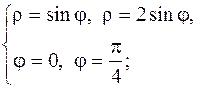
|
15. 
| 30. 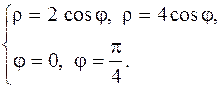
|
6. Найти центр тяжести плоской пластинки, ограниченной данными линиями, с помощью двойного интеграла
1. 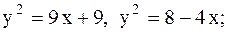
2. 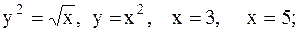
3. 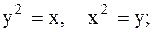
4. 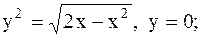
5. 
6. 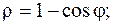
7. 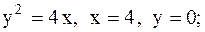
8. 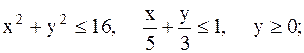
9. 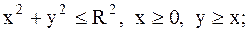
10. 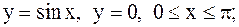
11. 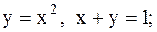
12.  (астроида)
(астроида) 
13. 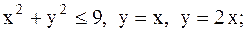
14. 
15. 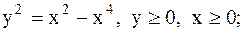
16. 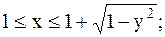
17. 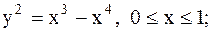
18. 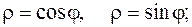
19. 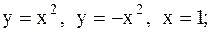
20. 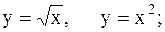
21. 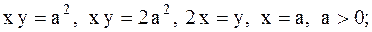
22. 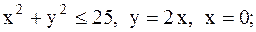
23. 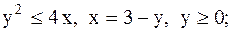
24. 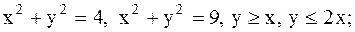
25. 
26. 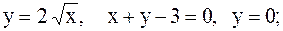
27. 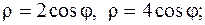
28. 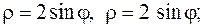
29.  (перейти в полярную систему координат);
(перейти в полярную систему координат);
30. 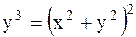 (перейти в полярную систему координат).
(перейти в полярную систему координат).
7. Найти объем тела, ограниченного указанными поверхностями, с помощью двойного интеграла: 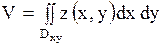
1. 
2. 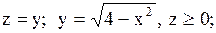
3. 
4. 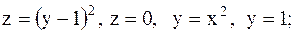
5. 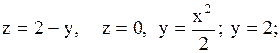
6. 
7. 
8. 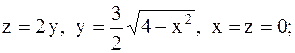
9. 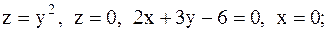
10. 
11. 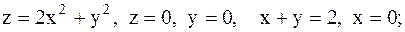
12. 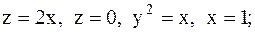
13. 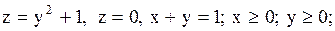
14. 
15. 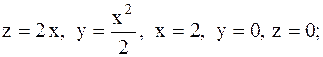
16. 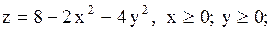 здесь (при вычислении двойного интеграла) надо сделать переход в полярную систему координат по формулам:
здесь (при вычислении двойного интеграла) надо сделать переход в полярную систему координат по формулам: 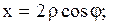
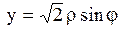 . Не забыть вычислить Якобиан.
. Не забыть вычислить Якобиан.
17. 
18. 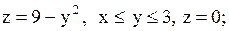
19. 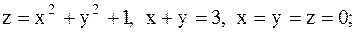
20. 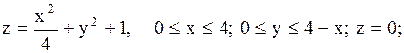
21. 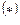
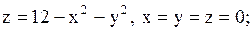
22. 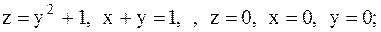
23. 
24. 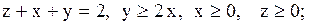
25. 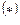
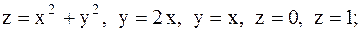
26. 
27. 
28. 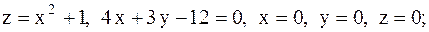
29. 
30. 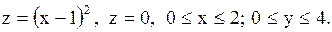
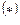 При вычислении двойного интеграла перейти в полярную систему координат.
При вычислении двойного интеграла перейти в полярную систему координат.
8 Вычислить тройной интеграл по заданной области интегрирования 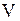
1. 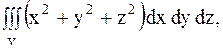
| 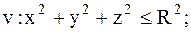
|
2. 
| 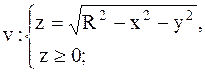
|
3. 
| 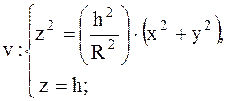
|
4. 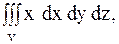
| 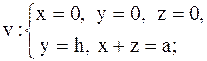
|
5. 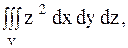
| 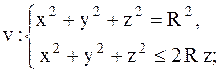
|
6. 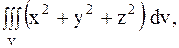
| 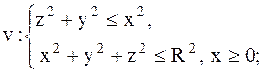
|
7.  
| 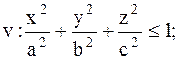
|
8. 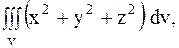
| 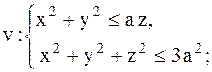
|
9. 
| 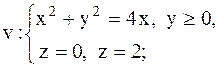
|
10. 
| 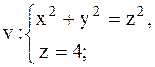
|
11. 
| 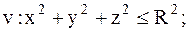
|
12. 
| 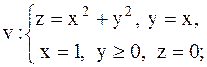
|
13. 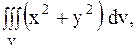
| 
|
14. 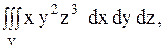
| 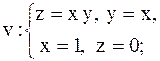
|
15. 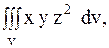
| 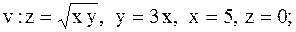
|
16. 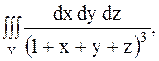
| 
|
17. 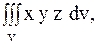
| 
|
18. 
| 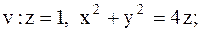
|
19.  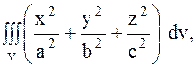
| 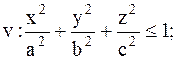
|
20. 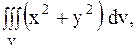
| 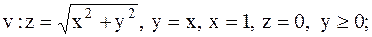
|
21. 
| 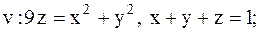
|
22. 
| 
|
23. 
| 
|
24. 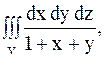
| 
|
25. 
| 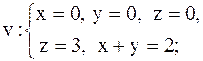
|
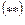 Сделать переход в сферическую систему координат по формулам: Сделать переход в сферическую систему координат по формулам:
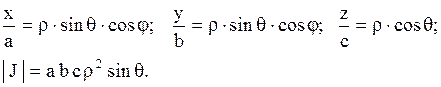
| |
26. 
| 
|
27. 
| 
|
28. 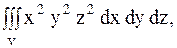
| 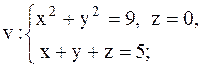
|
29. 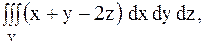
| 
|
30. 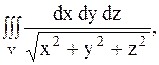
| 
|
9 Найти объем тела, заданного ограничивающими их поверхностями, с помощью тройного интеграла: 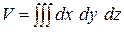
1. 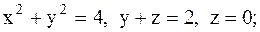
2. 
3. 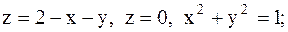
4. 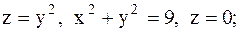
5. 
6. 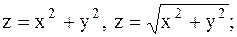
7. 
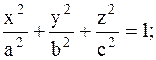
8. 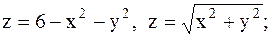
9. 
10. 
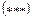 Сделать переход в сферическую систему координат по формулам:
Сделать переход в сферическую систему координат по формулам:
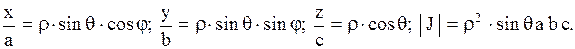
11. 
12. 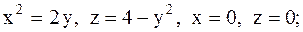
13. 
14. 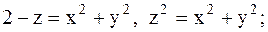
15. 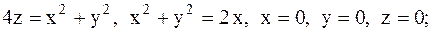
16. 
17. 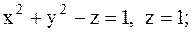
18. 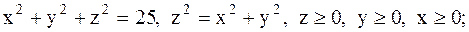
19. 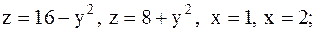
20. 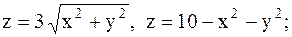
21. 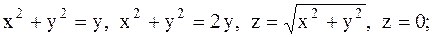
22. 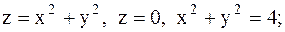
23. 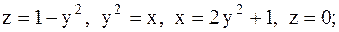
24. 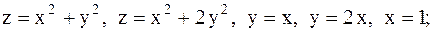
25. 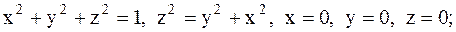
26. 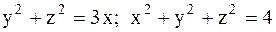 (внутренний объем по отношению к параболоиду);
(внутренний объем по отношению к параболоиду);
27. 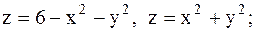
28. 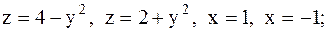
29. 
30. 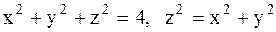 (вне конуса).
(вне конуса).
10. Тело задано ограничивающими его поверхностями, 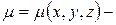 плотность массы тела. Найти центр тяжести тела с помощью тройного интеграла
плотность массы тела. Найти центр тяжести тела с помощью тройного интеграла
1. 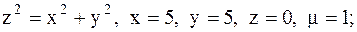
2. 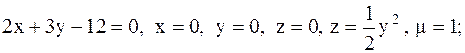
3. 
4. 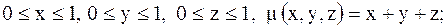
5. 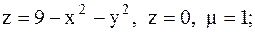
6. 
7. 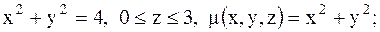
8. 
9. 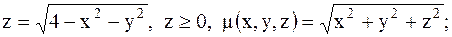
10. 
11. 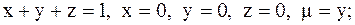
12. 
13. 
14. 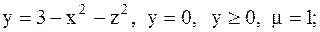
15. 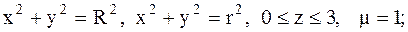
16. 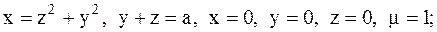
17. 
18. 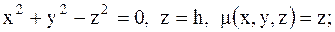
19. 
20. 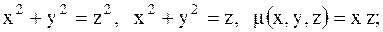
21. 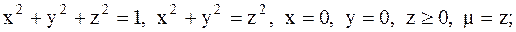
22. 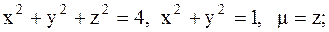
23. 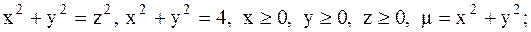
24. 
25. 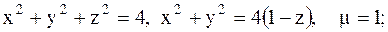
26. 
27. 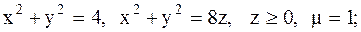
28. 
29. 
30. 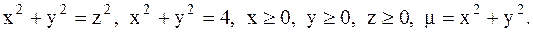
Вычислить криволинейный интеграл
1. 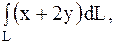
|  отрезок прямой от точки отрезок прямой от точки 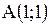 до до 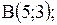
|
2. 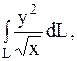
|  дуга дуга  от точки от точки 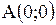 до до 
|
3. 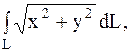
| 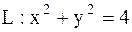
|
4. 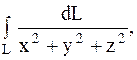
|  первый виток винтовой линии первый виток винтовой линии  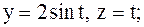
|
5. 
|  отрезок прямой от точки отрезок прямой от точки 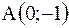 до до 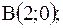
|
6. 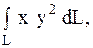
|  контур параллелограмма с вершинами контур параллелограмма с вершинами 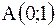 , , 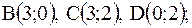
|
7. 
|  первая арка циклоиды первая арка циклоиды 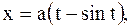 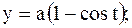
|
8. 
|  первый виток винтовой линии первый виток винтовой линии  , , 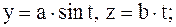
|
9. 
|  контур треугольника с вершинами контур треугольника с вершинами 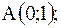 
|
10. 
|  контур треугольника с вершинами контур треугольника с вершинами
 , , 
|
11. 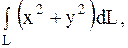
| 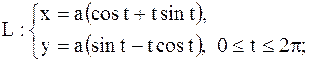
|
12. 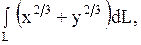
|  дуга дуга 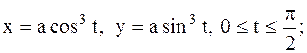
|
13. 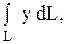
|  дуга эллипса дуга эллипса 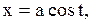 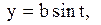
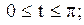
|
14. 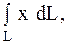
|  часть эллипса часть эллипса 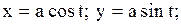 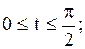
|
15. 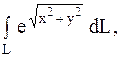
|  часть окружности часть окружности 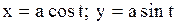 , находящаяся в 1-й четверти. , находящаяся в 1-й четверти.
|
16. 
|  часть цилиндрической винтовой линии часть цилиндрической винтовой линии 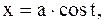 
|
17. 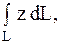
|  коническая винтовая линии коническая винтовая линии
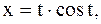 
|
18. 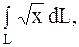
|  первая арка циклоиды первая арка циклоиды 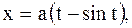 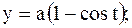
|
19. 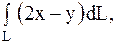
|  отрезок прямой от точки отрезок прямой от точки  до до 
|
20. 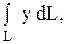
| 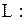 контур треугольника с вершинами контур треугольника с вершинами 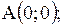  . .
|
21. 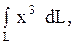
|  дуга дуга 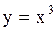 , находящаяся внутри окружности , находящаяся внутри окружности 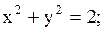
|
22. 
|  отрезок прямой, заключенный между точками отрезок прямой, заключенный между точками  и и 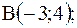
|
23. 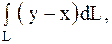
|  контур треугольника с вершинами контур треугольника с вершинами
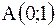 , , 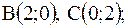
|
24. 
|  часть окружности часть окружности  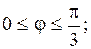
|
25. 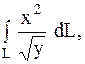
|  дуга линии дуга линии  от от  до до 
|
26. 
| 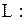 дуга эллипса дуга эллипса 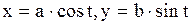 в 1-й четверти. в 1-й четверти.
|
27. 
| 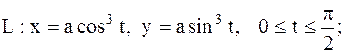
|
28. 
|  арка циклоиды арка циклоиды 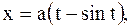

|
29. 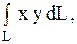
|  контур трапеции с вершинами контур трапеции с вершинами 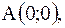 
|
30. 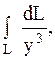
| 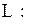 дуга эллипса дуга эллипса 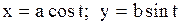 в 1-й четверти. в 1-й четверти.
|
12. Вычислить криволинейный интеграл по заданной линии 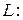
1. 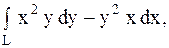
| 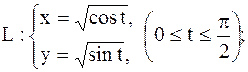
| |||||||||||||
2. 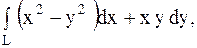
|  отрезок прямой от точки отрезок прямой от точки  до до 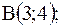
| |||||||||||||
3. 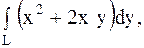
| 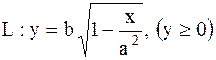 против часовой стрелки; против часовой стрелки;
| |||||||||||||
4. 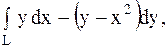
| 
| |||||||||||||
5. 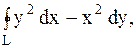
| 
| |||||||||||||
6. 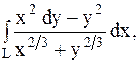
| 
| |||||||||||||
7. 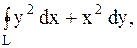
| 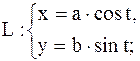
| |||||||||||||
8. 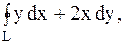
| 
| |||||||||||||
9. 
|  отрезок прямой от точки отрезок прямой от точки  до до 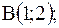
| |||||||||||||
10. 
|  контур треугольника с
вершинами контур треугольника с
вершинами  , , 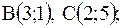
| |||||||||||||
11. 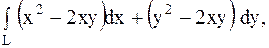
| 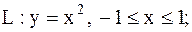
| |||||||||||||
12. 
|  ломаная ломаная  , где , где
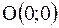 , ,
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-27 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |