Захарченко Анатолий Данилович 5 глава

 

Тема 2.1. Кинематика точки

 

В теоретической механике изучается простейшая форма движения материи – механическое движение, т.е. происходящее во времени изменение положения одного тела относительно другого.

Механическое движение – перемещение тела по отношению к другому телу, происходящее в пространстве и во времени.

Система отчета – любая система координат, связанная с телом отсчета.

Скорость – векторная величина, характеризующая быстроту и направления движения точки в данной системе отчета.

Тело отсчета – тело, относительно которого рассматривается движение других тел.

Траектория точки – геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета.

Ускорение – векторная величина, характеризующая изменение скорости по величине и направлению.

Пространство в механике рассматривается как трехмерное евклидово пространство. Время в классической механике предполагается универсальным, т.е. одинаковым во всех системах отсчета и не зависящим от движения.

В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы при различных способах задания движения.

 

2.1.1. Скорость точки

 

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 2.1). Положение движущейся точки М относительно рассматриваемой системы отсчета определяется в момент времени t радиус-вектором , который соединяет неподвижную точку О с этой точкой. В другой момент времени движущаяся точка займет положение и ее радиус-вектором будет . За время радиус-вектор движущийся точки изменится на .

Средней скоростью точки за время называют соотношение , т.е.

Средняя скорость параллельна вектору . В общем случае она зависит от времени осреднения . У нее нет конкретной точки приложения на участке траектории.

Введем скорость точки 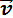в момент времени , которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т.е.

Скорость точки направлена в сторону ее движения по определенному направлению вектора при . Таким образом, скорость точки равна первой производной по времени от ее радиус-вектора. Она направлена по касательной к траектории в сторону движения точки.

Размерность скорости получаем из уравнения (2.2):

Часто скорость выражают в км/ч, например, скорость движения автотранспорта.

 

2.1.2. Ускорение точки

 

Пусть движущаяся точка М в момент времени t имеет скорость 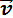. В момент времени эта точка занимает положение , имея скорость (рис. 2.2). Чтобы изобразить приращение скорости 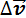за время , перенесём вектор скорости

параллельно самому себе в точку М.

Средним ускорением точки за время называют отношение , т.е. . Среднее ускорение точки параллельно приращению скорости 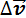. Как и средняя скорость, среднее ускорение не имеет на траектории конкретной точки приложения на участке и изображено в точке М условно. В общем случае среднее ускорение зависит от времени .

Ускорением точки в момент времени называют предел, к которому стремится среднее ускорение при , стремящемся к нулю, т.е.

Таким образом, ускорение точки равно первой производной по времени от скорости точки. Ускорение точки направлено внутрь вогнутости траектории.

Размерность ускорения в СИ получаем из (2.3):

 

2.1.3. Векторный способ изучения движения

 

Изучить движение точки означает: задать (определить) уравнения движения; определить траекторию, скорость и ускорение точки.

Существуют три способа изучения движения точки – векторный, координатный и естественный.

Движение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиус-вектором этой точки (рис. 2.3). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т.е.

(2.4)

Траекторией точки является годограф радиус-вектора. Скорость точки направлена по касательной к траектории и вычисляется, согласно её определению, по формуле

Векторный способ ввиду его краткости и компактности удобен для теоретического изложения кинематики точки. Для практического вычисления скорости и ускорения обычно используют координатный и естественный способы изучения движения точки.

 

2.1.4. Координатный способ изучения движения

 

Задание движения и траектория

Движение точки можно изучать, используя любую систему координат. Рассмотрим случай декартовых прямоугольных осей координат, которые являются также системой отсчета. Движение точки в декартовых координатах считается заданным, если известны координаты точки как непрерывные, дважды дифференцируемые функции времени (рис. 2.4), т.е. заданы уравнения движения точки в декартовых координатах:

Уравнения движения позволяют найти положение точки, ее скорость и ускорение в любой момент времени. Уравнения движения (2.6) есть также уравнения траектории точки в параметрической форме, параметром является время t.

Уравнения траектории в координатной форме из выражения (2.6) получают исключением параметра t. Исключая время, получим уравнения двух поверхностей:

(2.7)

Траекторией является линия пересечения этих поверхностей.

Скорость в декартовых координатах

Разложим радиус-вектор и скорость точки на составляющие, параллельные осям координат (рис. 2.5), получим:

где x, y, z – координаты точки М; 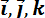– единичные векторы осей координат; проекции скорости на оси координат.

Учитывая выражение (2.8), согласно определению скорости, имеем

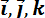не изменяются при движении точки М. Сравнивая (2.8) и (2.9), получаем для проекций скорости на декартовы оси координат следующие формулы:

По проекциям определяют числовую величину (модуль) скорости и косинусы углов вектора скорости с осями координат:

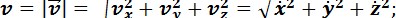
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим

соответственно

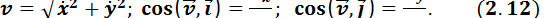
Для прямолинейного движения точки координатную ось, например Ox, направляют по траектории (рис. 2.6).

 

 

Тогда

(2.13 )

Проекция скорости и ее модуль определяются по следующим формулам:

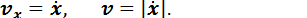(2.14)

Ускорение точки в декартовых координатах

Разложим ускорение точки на составляющие, параллельные осям декартовой системы координат:

(2.15)

где - проекции ускорения на координатные оси. Согласно определению ускорения и формулам (2.9) и (2.10), имеем

Сравнивая выражения (2.15) и (2.16), получаем формулы для проекции ускорения на оси декартовой системы координат:

Числовую величину ускорения и косинусы углов вектора ускорения с осями координат определяем по формулам:

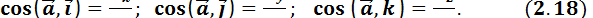
При движении точки по плоскости оси Ox и Oy выбирают в этой плоскости. Тогда .

Формулы для ускорения и его проекции на оси координат примут вид

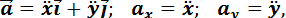
соответственно

Для прямолинейного движения ось Ox направим по траектории точки. Тогда:

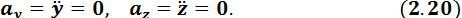
Формулы для ускорения и его проекции на ось Ox принимают вид

Соответственно для числовой величины ускорения имеем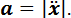

 

2.1.5. Естественный способ изучения движения

 

· Естественный способ задания движения

При естественном способе задания движения задаются траектория точки, начало и направление отсчета дуговой координаты и уравнение движения точки по траектории.

Для задания закона движения точки по траектории необходимо выбрать на траектории точку О, принимаемую за начало отсчета расстояний (рис. 2.7). Расстояния в одну сторону от точки О по траектории считаются положительными (например, вправо), в другую – отрицательными. Кроме того, следует задать начало отсчета времени.

Закон движения точки по траектории задается зависимостью от времени расстояния s, отсчитываемого от точки О до точки M, т.е. (2.21)

Расстояние s (дуговая координата) берется по траектории, его не следует отождествлять с пройденным точкой путем.

· Скорость точки при естественном способе задания движения

Пусть движение точки заданно естественным способом. Вычислим скорость точки. Для этого используем радиус-вектор движущейся точки, начало которого находится в неподвижной точке (рис. 2.8).

При движении точки ее радиус-вектор изменяется с течением времени, а следовательно, он изменяется в зависимости от дуговой координаты. Используя определение скорости, имеем

 

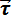или , где . Вектор направлен по касательной к траектории как производная от вектора по скалярному аргументу и является единичным вектором. Единичный вектор 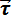всегда направлен по касательной к траектории в сторону положительного отсчета координаты s независимо от направления движения точки. При вектор скорости направлен по 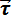; при он имеет направление, противоположное 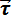. Величина называют алгебраической скоростью точки. Ее можно считать проекцией скорости на положительное направление касательной к траектории, совпадающее с направлением единичного вектора .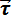

· Естественные оси координат

Построим в точке М кривой линии естественные оси этой кривой (рис. 2.9). Первой естественной осью является касательная . Ее положительной направление совпадает с направлением единичного вектора касательной .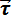

Перпендикулярно касательной располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью. Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью. По главной нормали внутрь вогнутости кривой направим единичный вектор . Он определяет положительной направление второй естественной оси. Нормаль, перпендикулярная главной нормали и расположенная в нормальной плоскости, называется бинормалью. Единичный вектор , направленный по бинормали так, чтобы три вектора образовывали правую систему осей координат, определит положительной направление третьей естественной оси.

Три взаимно перпендикулярные оси положительные направления которых совпадают с направлениями единичных векторов , называются естественными осями кривой.

Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется

 

вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой. · Ускорение точки при естественном способе задания движения Учитывая, что для скорости точки имеем

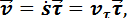Рис.2.9

в соответствии с определением ускорения получаем

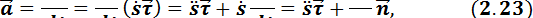
где .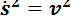

Получено разложение ускорения точки по осям естественного трехгранника. Часть ускорения

называется касательной составляющей ускорения. Другая часть ускорения

называется нормальной составляющей ускорения. Она направлена внутрь вогнутости траектории, т.е. в сторону положительного направления единичного вектора главной нормали . Таким образом, ускорение точки имеет вид

Из (2.23) получим формулы для проекций ускорения на естественные оси, т.е.

Проекция ускорения на положительное направление касательной, совпадающее с направлением единичного вектора 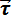, называется касательным ускорением, а главную нормаль, направленную по единичному вектору , нормальным ускорением. Проекция ускорения на бинормаль равна нулю, следовательно, ускорение точки расположено в соприкасающейся плоскости траектории.

Учитывая ортогональность 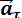и (рис. 2.10), в соответствии с формулой (2.30) имеем

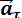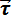Нормальная составляющая ускорения всегда направлена внутрь вогнутости траектории. Касательная составляющая при направлена в положительную сторону касательной, т.е. по направления единичного вектора , при в отрицательную, противоположно .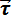

Случаи обращения в нуль касательного ускорения получают из условия

Это условие выполняется все время, пока т.е. при равномерном движении точки по траектории любой формы. Касательное ускорение обращается в нуль также в те моменты времени, в которые алгебраическая скорость достигает экстремума.

Случаи обращения в нуль нормального ускорения следуют из условия

Это условие выполняется при , т.е. при прямолинейном движении точки, а также при движении точки по криволинейной траектории в точках перегиба, в которых происходит изменение выпуклости траектории на вогнутость и наоборот (рис. 2.11).

Нормальное ускорение обращается в нуль в моменты времени, в которые , т.е. в моменты изменения направления движения точки по траектории.

Касательное ускорение характеризует изменение вектора скорости по величине, а нормальное – по направлению.

 

Тема 2.2. Простейшие движения твердого тела

 

Различают два простейших вида движения тела, комбинированием которых можно получать другие, более сложные его движения. Такими движениями твердого тела являются поступательное движение и вращение твердого тела вокруг неподвижной оси.

 

2.2.1. Степени свободы и теорема о проекциях скоростей

 

Числом степеней свободы твердого тела называют число независимых параметров, определяющих положение тела относительно рассматриваемой системы отсчета.

Движение твердого тела во многом зависит от числа его степеней свободы. Свободное твердое тело в общем случае имеет шесть степеней свободы. В качестве независимых параметров можно взять любые шесть координат точек или шесть других независимых параметров, которые являются функциями координат трех или большего количества точек тела. У свободной точки три независимые степени свободы, и соответственно, три независимых параметра, например ее координаты x, y, z. Точка, которая движется по неподвижной поверхности, имеет две степени свободы. При движении по неподвижной кривой точка имеет одну степень свободы.

Справедлива следующая теорема.

При любом движении твердого тела проекции скоростей точек на прямую, соединяющую эти точки, равны (рис. 2.12).

Для доказательства теоремы используем зависимость радиус-векторов точек А и В:

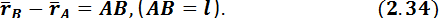
Возведем обе части в скалярный квадрат:

но l = const для твердого тела. Дифференцируя по времени это выражение, справедливое для любого момента времени, получим

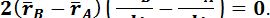
Заменив в этом равенстве

получим

Раскрывая произведения векторов и сокращая их на l,имеем

(2.35)

Теорема доказана. Очевидно, все точки тела, расположенные на прямой АВ, имеют одинаковые проекции скоростей на эту прямую.

 

2.2.2. Поступательное движение твердого тела

Поступательным движением твердого тела называют такое его движение, при котором любая прямая, жестко скрепленная с телом, остается параллельной своему первоначальному положению в каждый момент времени.

Траектории точек у поступательного движущегося твердого тела могут быть не только прямыми, но и любыми кривыми, в том числе окружностями.

Свойства поступательного движения характеризует следующая теорема.

При поступательном движении твердого тела траектории, скорости и ускорения точек тела в любой фиксированный момент времени одинаковы.

Если выбрать две точки А и В твердого тела, то радиус-векторы этих точек удовлетворяют условию (рис. 2.13)

Для любого твердого тела вектор является постоянным по модулю, а при поступательном движении он не изменяется и по направлению.

Уравнение (2.36) показывает, что годограф радиус-вектора точки В, являющийся траекторией этой точки, сдвинут по сравнению с годографом радиус-вектора точки А (траектория точки А) на постоянный вектор . Если этот сдвиг осуществить, то обе траектории совпадут всеми своими точками. такие траектории называют конгруэнтными (одинаковыми).

Если продифференцировать по времени уравнение (2.36), справедливое для любого момента времени, то получим

В этом равенстве . Кроме того, производная от постоянного по модулю и направлению вектора имеет вид

Таким образом, для любого момента времени имеем

Дифференцируя по времени уравнение (2.12) и учитывая, что

получим

(2.38)

Так как точки А и В выбраны произвольно, то эти равенства справедливы для всех точек твердого тела. Теорема о поступательном движении твердого тела полностью доказана.

Поступательное движение твердого тела полностью характеризуется движением любой точки тела.

 

2.2.3. Вращательное движение твердого тела вокруг неподвижной оси

· Угол поворота, угловая скорость и ускорение

Вращением твердого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. при этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.

Если А и В – неподвижные точки тела (рис. 2.14), то осью вращения является ось Oz. Через ось вращения проведем плоскости: неподвижную и подвижную П, скрепленную с вращательным телом. Пусть в начальный момент времени обе плоскости совпадают. Тогда в момент времени t положение подвижной плоскости и самого вращающегося тела можно определить двухгранным углом между плоскостями и соответствующим линейным углом 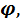расположенными в этих плоскостях и перпендикулярными оси вращения. Угол называется углом поворота тела.

Положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени, если задано уравнение

(2.39)

Это уравнение называют уравнением вращения твердого тела вокруг неподвижной оси. У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла . Угол считается положительным, если он откладывается против часовой стрелки, и отрицательным – если в противоположном направлении, если смотреть с положения направления оси Oz. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных оси вращения.