Определение. Производная от первой производной называется второй производной и обозначается 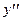 или
или 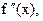 или
или 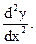 Аналогично определяются производные третьего и так далее порядков.
Аналогично определяются производные третьего и так далее порядков.
Пример 31.1. 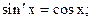

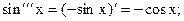
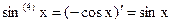 . Теперь легко догадаться, что
. Теперь легко догадаться, что 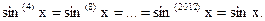 (Обратите внимание, как обозначается производные).
(Обратите внимание, как обозначается производные).
Дифференциалы различных порядков
Определение. Дифференциал от дифференциала первого порядка называется дифференциалом второго порядка и обозначается 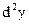 . Аналогично определяются дифференциалы третьего и т.д. порядков. Обозначим
. Аналогично определяются дифференциалы третьего и т.д. порядков. Обозначим 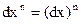 .
.
Теорема. Если 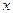 - независимый аргумент, то
- независимый аргумент, то 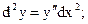 ...;
...; 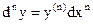 .
. 
Пример 32.1. 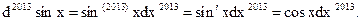
Свойства непрерывных функций
Теорема 33.1.(Теорема Больцано-Коши; чеш. математик и философ 1781-1848; франц. математик 1789-1857). Пусть функция 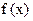 определена и непрерывна на отрезке
определена и непрерывна на отрезке 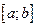 и
и 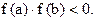 Тогда существует точка
Тогда существует точка 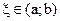 такая, что
такая, что 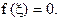
Пример 33.1. Пусть 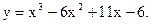 Очевидно, что
Очевидно, что 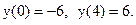 Поэтому можно утверждать, что на интервале (0;4) график данной функции хотя бы один раз пересекает ось абсцисс. (В действительности три раза пересекает ось абсцисс при х=1, х=2, х=3, рис. 33.1).
Поэтому можно утверждать, что на интервале (0;4) график данной функции хотя бы один раз пересекает ось абсцисс. (В действительности три раза пересекает ось абсцисс при х=1, х=2, х=3, рис. 33.1).
Теорема 33.2. (Теорема Вейерштрасса; нем. математик 1815-1897). Пусть функция 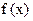 определена и непрерывна на отрезке
определена и непрерывна на отрезке 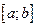 . Тогда
. Тогда 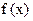 ограничена на этом отрезке.
ограничена на этом отрезке.
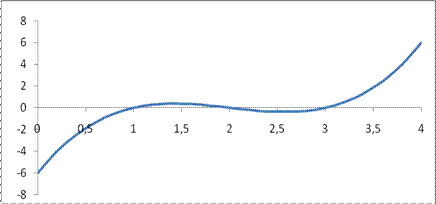 Рис. 33.1.
Рис. 33.1.
Пример 33.2. На рис. 33.1 дан график функции 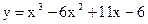 . Функция на отрезке [0,4] непрерывна. Значит на интервале (0,4) она не может принимать сколь угодно большие значения.
. Функция на отрезке [0,4] непрерывна. Значит на интервале (0,4) она не может принимать сколь угодно большие значения.
Теорема 33.3. (Теорема Ролля; франц. математик 1652-1719). Пусть функция 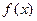 определена и непрерывна на отрезке
определена и непрерывна на отрезке 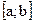 , дифференцируема в каждой точке интервала
, дифференцируема в каждой точке интервала 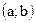 и
и 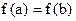 . Тогда существует точка
. Тогда существует точка 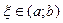 такая, что
такая, что 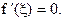
Пример 33.1. На рисунке 33.3 дан график функции
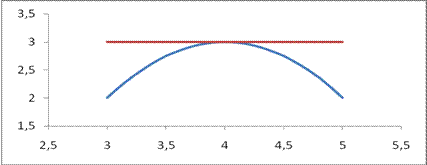
Рис. 33.3.
 Т.К. функция непрерывна на отрезке [3,5], диффуренцируема внутри этого отрезка и
Т.К. функция непрерывна на отрезке [3,5], диффуренцируема внутри этого отрезка и 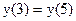 . Поэтому внутри отрезка [3,5] найдется по крайней мере одна точка, в которой касательная горизонтальна.
. Поэтому внутри отрезка [3,5] найдется по крайней мере одна точка, в которой касательная горизонтальна.
Теорема Лагранжа
(франц. математик 1736-1813)
Теорема. Пусть функция 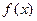 определена и непрерывна на отрезке
определена и непрерывна на отрезке 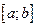 и дифференцируема в каждой точке интервала
и дифференцируема в каждой точке интервала 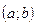 . Тогда существует точка
. Тогда существует точка 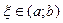 такая, что
такая, что 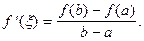
Пример 34.1. На рис. 34.1 дан график функции 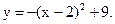 Рассмотрим участок графика между точками A(0;5) и В(2;9). Т.к. наша функция удовлетворяет условиям теоремы, то теорема Лагранжа утверждает, что на интервале найдется (по крайней мере одна) точка, через которую проведенная касательная параллельна прямой, проходящей через точки А и В.
Рассмотрим участок графика между точками A(0;5) и В(2;9). Т.к. наша функция удовлетворяет условиям теоремы, то теорема Лагранжа утверждает, что на интервале найдется (по крайней мере одна) точка, через которую проведенная касательная параллельна прямой, проходящей через точки А и В.
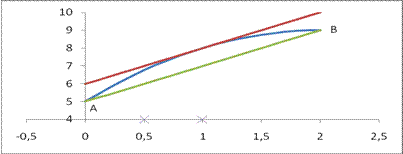
Рис. 34.1.
Возрастание (убывание) функции
Определение. Функция 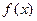 называется возрастающей на
называется возрастающей на 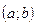 , если для любых точек
, если для любых точек 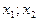 , удовлетворяющих
, удовлетворяющих 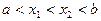 ,выполняется неравенство
,выполняется неравенство 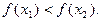
Определение. Функция 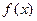 называется убывающей на
называется убывающей на 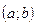 , если для любых точек
, если для любых точек 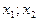 , удовлетворяющих
, удовлетворяющих 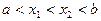 , выполняется неравенство
, выполняется неравенство 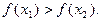
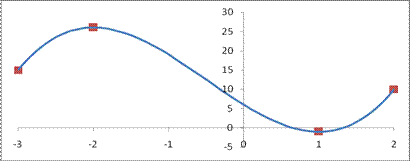
Рис. 35.1.
Пример 35.1. На рисунке 35.1 дан (на отрезке
[-3;2]) график функции 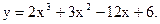 Очевидно, что на отрезках [-3,-2] и [1,2] функция возрастает, а на отрезке [-2,1] убывает.
Очевидно, что на отрезках [-3,-2] и [1,2] функция возрастает, а на отрезке [-2,1] убывает.
Необходимые условия возрастания (убывания) функции
Теорема. Если функция дифференцируема и возрастает (убывает) на 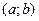 , то
, то 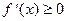 (
(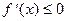 )
) 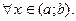
Пример 36.1. Функция, график которой указан на рис.36.1, возрастает на отрезке [-3,-2]. Поэтому тангенс угла наклона касательной (на этой части графика) не может быть отрицательным. При х=-2 тангенс угла наклона касательной равен нулю: 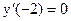 (касательная горизонтальная, см. рис. 36.1).
(касательная горизонтальная, см. рис. 36.1).
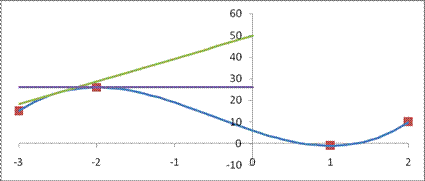
Рис. 36.1.