Теорема. Пусть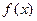 
непрерывна в некоторой 
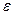окрестности точки 
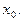Тогда, если при переходе через точку 
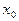производная 
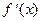меняет знак, то функция в точке 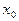имеет экстремум. При этом, если 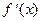меняет знак с минуса на плюс, то в точке 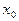минимум. Если 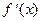меняет знак с плюса на минус, то в точке 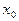максимум.
Пример 42.1. Еще раз проанализируем рис. 37.1:
левее точки (-2,26) производная положительна (так как тангенс угла наклона касательной больше нуля). Правее от этой точки производная отрицательна. Иначе говоря, при переходе через точку (-2,26) производная меняет знак с плюса на минус. Поэтому точка (-2,26) является точкой максимума. Что касается точки (1,-1), то при переходе через нее производна меняет знак с минуса на плюс. Поэтому точка (1,-1) является точкой минимума.
Пример 42.2. При переходе через точку (0,0) (см. рис. 41.1) производная не меняет знак (слева плюс и справа плюс). Поэтому (0,0) не является точкой экстремума.
Пример 42.3. На рис. 41.3 точка (0,0) является точкой минимума, т.к. слева производна отрицательна, а справа положительна.
Выпуклость графика функции
Определение. Кривая называется выпуклой «вверх» («вниз») 
в некотором интервале 
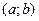, если на этом интервале кривая находится «ниже» («выше») (кроме точки 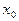) любой касательной, проведенной в любой точке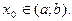 
Выпуклость вверх будем обозначать 
(правильное расположение зонтика), а выпуклость вниз - 
(неправильное расположение зонтика).
Пример 43.1. Рассмотрим график функции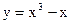 
:
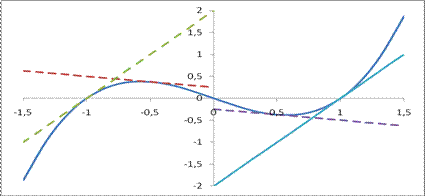
Рис. 43.1.
На промежутке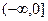 
функция выпукла вверх, т.к. на этом промежутке график находится ниже любой касательной. На промежутке 
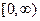функция выпукла вниз, т.к. график находится выше любой касательной.
Необходимые условия выпуклости
Теорема. Если на 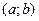функция выпукла «вверх» («вниз») и дважды дифференцируема, то 
(
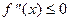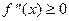) для всех 
.
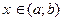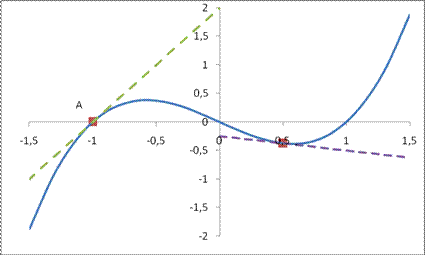
Рис. 44.1.
Пример 44.1. На промежутке 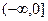функция 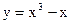выпукла вверх. Если точку касания А (см. рис. 44.1) будем передвигать слева направо, то касательная будет поворачиваться по часовой стрелке. Значит тангенс угла наклона касательной будет убывать. Т.е. первая производная будет убывать. Отсюда следует, что вторая производная неположительная (см. §36). Проверьте, что вторая производная в точке х=0 равняется нулю. Аналогично рассуждаем для промежутка 
.
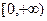Достаточные условия выпуклости
Теорема. Если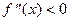 
(
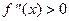) на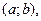 
то на этом интервале функция выпукла «вверх» («вниз»).
Пример 45.1. Определим направления выпуклости функции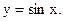 
Находим 
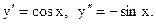Из школьного курса следует, что при 
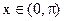вторая производная 
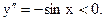При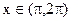 
вторая производная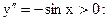 
Рис. 45.1.
Поэтому на интервале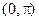 
функция выпукла вверх, а на интервале 
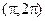- вниз:
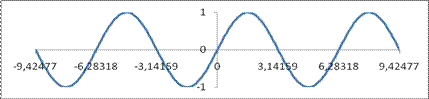
Рис. 45.2.
Пользуясь периодичностью делаем вывод, что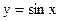 
выпукла вверх при 
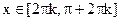и выпукла вниз при 
.
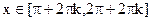Определение точки перегиба
Определение. Точка 
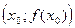называется точкой перегиба функции, если при переходе через эту точку функция меняет выпуклость «вверх» на выпуклость «вниз» (или выпуклость «вниз» на выпуклость «вверх»).
Пример 46.1. Точки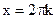 
являются точками перегиба функции 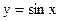, т.к. при переходе через эти точки меняется направление выпуклости. Например слева от х=0 функция 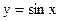выпукла вниз, а справа от х=0 – выпукла вверх: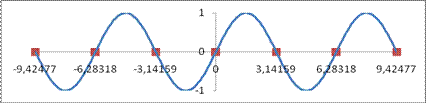 
Рис. 46.1.