Частные производные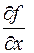 
и 
представляют собой производные от функции z=f(x,y) по двум частным направлениям осей О X и О Y. Пусть z=f(x,y) – дифференцируемая функция в некоторой области D, М(х 0, у 0)ÎD. Пусть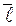 
- некоторое направление (вектор с началом в точке М), а 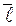=(cos a, cos b) – орт этого направления. Тогда производная функции z=f(x,y) по направлению 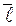в точке М(х 0, у 0) вычисляется по формуле:
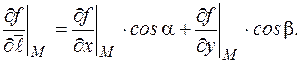Если вектор 
, то 
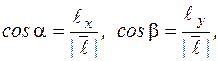где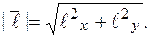 
Теорема 1. Производная по направлению, касательному к линии уровня поверхности z=f(x,y), равна нулю.
По аналогии со случаем функции двух переменных можно определить производную по направлению для функции трех переменных u=f(x,y,z).
, где cos a, cos b, cos g - направляющие косинусы направления .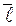
Теорема 2. Производная по направлению, касательному к поверхности уровня функции u=f(x,y,z), равна нулю.
Градиентом функции z=f(x,y) называется вектор с координатам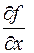и и . Обозначение: 
.
Теорема 3. Имеет место равенство 
= 
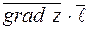, т.е. производная по направлению 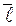равна скалярному произведению векторов градиента и орта направления .
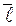Следствие. Вектор 
в каждой точке направлен по нормали к линии уровня, проходящей через данную точку, в сторону возрастания функции. При этом
.
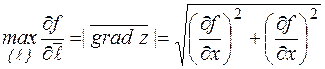Теорема 4. Скорость изменения функции f по некоторому направлению 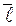равна проекции вектора градиента на это направление, т.е. = 
. В случае функции u=f(x,y,z) градиент функции равен 
.
_____________________________
1. Найти производную функции z=x 2 -xy+y 2 в точке М (1;1) в направлении вектора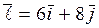 
.
2. Найти производную функции u=xy 2 z 3в точке М(3;2;1) в направлении вектора 
, где N(5;4;2).
3. Найти производную функции z=ln(x 2 +y 2) в точке М(3;4) в направлении градиента функции z.
4. Найти величину u направление градиента функции u=xyz в точке М(2;1;1).
______________________________
5. Найти производную функции u=ln(x 2 +y 2+ z 2) в точке М(1;2;1) в направлении вектора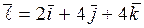 
и gradu в точке М.
6. Найти производную функции z= 3 x 2 + 5 y 2 в точке А(1;-1) по направлению к точке В(2;1) и gradz в точке А.
_______________________________
Ответы: 1) 1,4; 2)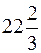 
; 3) 0,4; 4)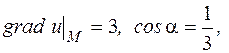 
5) 
; 6) 
.
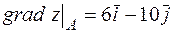Экстремум функции двух переменных
Рассмотрим функцию z=f(x,y) двух переменных, определенную в некоторой области D. Функция f(x,y) имеет строгий локальный максимум (минимум) в точке М0(х 0, у 0), если неравенство f (х 0, у 0)> f (х, у), (f (х 0, у 0)< f (х, у)) имеет место во всех точках М(х, у)¹М0 из некоторой достаточно малой окрестности точки М0.
Вопрос определения экстремумов (максимумов или минимумов) в некоторых случаях решается просто, если f(x,y) дифференцируемая функция в окрестности точек экстремума.
Теорема (необходимые условия экстремума). Если f(x,y) – дифференцируема в точке (х 0, у 0) и имеет экстремум в этой точке, то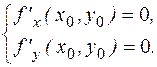 
Точка (х 0, у 0) называется стационарной точкой функции f (х, у). Пусть (х 0, у 0) – стационарная точка функции f(x,y). Обозначим
.
Теорема (достаточные условия экстремума).
1) Если АС-В 2>0 и A <0, то (х 0, у 0) – точка максимума.
2) Если АС-В 2>0 и A >0, то (х 0, у 0) – точка минимума.
3) Если АС-В 2<0, то (х 0, у 0) – не является точкой экстремума.
4) Если АС-В 2=0, то точка М0(х 0, у 0) может как быть, так и не быть точкой экстремума, поэтому требуется дополнительное исследование.
________________________________
Исследовать функции на экстремум:
1. 
.
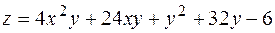2. 
.
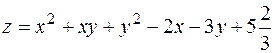3. 
.
4. 
.
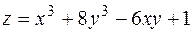5. 
.
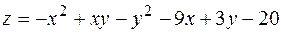6. 
.
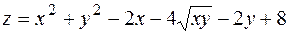Ответы: 1). zmin( -3;2)= -10. 2) zmin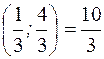 
. 3) zmin (4;4)=12. 4) zmin 
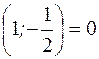. 5) zmin (-5;-1)=1. 6) zmin (2;2)=0.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. Письменный, Д.Т. Конспект лекций по высшей математике/ Д.Т. Письменный. – 6-е изд. – М.: Айрис-пресс, 2006-288с.
2. Минорский, В.П., Сборник задач по высшей математике: учеб.пособ. для втузов/ В.П. Минорский. – М.:Физ.мат.лит., 2004.
Дополнительная
1. Данко, П.Е. Высшая математика в упражнениях и задачах/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Оникс 21 век, Мир и образование, 2005 – 242с.
2. Лунку, К.Н. Сборник задач по высшей математике/ К.Е. Лунку. – М.: Айрис-пресс, 2009 – 592с.