Любой объект исследований зависит от многих действующих на него факторов, которые затрудняют его исследование. Например, массив горных пород является сложной физической средой и обладает целым рядом структурно-механических особенностей, которые в значительной степени определяет его механическое состояние. Изучение таких объектов и процессов, происходящих в них, производят с помощью метода моделирования, основанного на замене реального объекта его моделью, отображающей с определенной точностью основные свойства оригинала и специально создаваемой для их изучения.
Моделирование как метод научного исследования получило широкое развитие с середины XIX века. Однако уже задолго до этого некоторые ученые на основе интуитивных соображений обращались к натурным моделям. Систематическое моделирование оказалось возможным благодаря разработке научных положений теории подобия, которая явилась основой применения физических моделей (модель и оригинал имеют одинаковую физическую природу) во всех областях науки. Однако физическое моделирование имеет ограниченную сферу применения. Более широкими возможностями обладает математическое моделирование, под которым понимают способ исследования различных объектов путем изучения явлений (процессов), имеющих различное физическое содержание, но описываемых одинаковыми математическими соотношениями. В простейших случаях для этой цели используются известные аналогии между механическими, электрическими, тепловыми и другими явлениями.
Существенным моментом математического моделирования является то обстоятельство, что при изучении любого явления (процесса), в первую очередь, необходимо построить его математическое описание, или, иными словами, составить математическую модель. При аналоговом моделировании математическая модель позволяет для данного процесса-оригинала подобрать на основании известных аналогий удобные физические процессы – модели, а также установить соотношения, связывающие их параметры. В более сложных случаях, когда для моделирования создаются специальные установки или используются ЭВМ, математическая модель необходима для определения структуры объекта и параметров стенда или построения моделирующего алгоритма на одном из языков программирования.
Математическая модель реальной системы является абстрактным формально описанным объектом, изучение которого возможно математическими методами, в том числе и с помощью математического моделирования. Сложность и многообразие процессов функционирования реальных систем не позволяет строить для них абсолютно адекватные математические модели. Поэтому обычно математическая модель, описывающая процесс функционирования системы, в состоянии охватить только основные, характерные его закономерности, оставляя в стороне второстепенные факторы.
Формализации любого реального процесса предшествует изучение структуры составляющих его явлений. В результате этого производится так называемое содержательное описание процесса, представляющее собой первую попытку изложения закономерностей и постановку прикладной задачи. Оно является исходным для последующих этапов формализации, т.е. построения формализованной схемы процесса и математической модели.
Содержательное описание концентрирует сведения о физической природе и количественных характеристиках элементарных явлений исследуемого процесса, о степени и характере взаимодействия между ними, о месте и значении каждого явления в общем процессе функционирования системы. Процесс может быть описан лишь в результате обстоятельного его изучения, которое зачастую сводится к наблюдению за ним и фиксации количественных характеристик при проведении эксперимента. Однако иногда требуется составление описания процессов, для которых измерения невозможны. В этих случаях используют накопленный опыт и результаты наблюдений за аналогичными процессами.
В содержательное описание включают постановку прикладной задачи, определяющую цель моделирования исследуемого процесса, перечень искомых величин с указанием их практического предназначения и требуемой точности. Постановка прикладной задачи обычно не имеет строгой математической формулировки. Однако она должна обязательно содержать четкое изложение идеи предполагаемого исследования, перечень зависимостей, подлежащих оценке по результатам моделирования, совокупность факторов, которые должны учитываться при построении математической модели процесса.
Формализованная схема процесса является промежуточным звеном между содержательным описанием и математической моделью. Она разрабатывается в тех случаях, когда из-за сложности объекта переход от содержательного описания к математической модели оказывается невозможным. Для построения формализованной схемы необходимо выбрать характеристики процесса, установить систему параметров, определить все зависимости между характеристиками и параметрами процесса, с учетом факторов, учитываемых при формализации. На этом этапе должна быть дана точная математическая формулировка задачи исследования с указанием окончательного перечня искомых величин и оцениваемых зависимостей. Математическая формулировка основывается на начальных условиях и систематизированной совокупности всех исходных данных, которые могут быть представлены графически или таблично, но с обязательным решением вопросов интерполяции и экстраполяции экспериментального материала.
Преобразование формализованной схемы в математическую модель выполняется математическими методами, для этого все соотношения выражаются в аналитической форме, записываются в виде систем неравенств логические условия. При моделировании процессов на ЭВМ числовой материал используется не в первоначальном виде, а в форме аппроксимирующих выражений (интерполяционных полиномов). При построении математических моделей необходимо очень осторожно подходить к приближенным зависимостям, представляющим экспериментальные данные, так как это обстоятельство может играть заметную роль с точки зрения совпадения результатов моделирования.
Таким образом изучить объект наиболее полно можно лишь при условии, если модель полностью отражает его физическую сущность или может быть представлена в математическом виде. Рассмотрим несколько примеров по составлению моделей для исследования явлений и процессов в области горной науки.
Реологическая модель породного массива. При исследовании процессов в массиве горных пород распространение получила теория упруго-вязко-пластической среды, в которой для наглядности изображения реологических свойств породы используется метод структурных моделей. Общий вид модели для линейнодеформируемой среды приведен на рис. 4.1. Каждая из таких моделей включает в себя простейшие элементы, имитирующие упругие, вязкие и пластические свойства. Упругие свойства среды имитируются пружинами (рис. 4.2, а), деформирование которых подчиняется закону Гука (
– величина деформации прямо пропорциональна приложенной нагрузке, где Е – модуль Юнга). Движение перфорированного поршня в заполненном вязкой жидкостью цилиндре (рис.4.2, б), характеризует вязкие свойства тел согласно закону Ньютона, (
– сопротивление пропорционально скорости деформирования, где h – коэффициент вязкости). Пластические свойства среды учитываются, моделью пластичности Сен-Венана (рис. 4.2, в), представляющей собой груз, скольжение которого по площадке возможно, если 
, где 
– определенная константа для данной среды.
 |  | ||
Математическая модель, соответствующая приведенной на рис. 4.1 физической модели, имеет сложный вид. Поэтому рассмотрим входящую в ее состав более простую модель вязко-упругого тела (модель Максвелла), широко применяемую в механике горных пород для описания поведения глин (рис. 4.3). Деформация тела в соответствии с моделью Максвелла состоит из суммы двух членов, один из которых связан с напряжением уравнением упругости Гука, а производная второго связана с напряжением с помощью уравнения вязкости Ньютона. Модель Максвелла представляет собой последовательное соединение двух простых механических элементов (Гука и Ньютона). В этом случае математическая модель, соответствующая физической модели (рис. 4.3), принимает вид:
. (4.3)
Решая (4.3) при s = const, получим уравнение ползучести
, (4.4)
где h = Е 0 t 0;
Е 0 – мгновенный модуль упругости;
t 0 – время релаксации, в течение которого напряжения уменьшаются в е раз;
ε 0 = s/ Е 0 – начальная деформация.
Решая (4.3) при ε = const, получим уравнение релаксации
, (4.5)
где σ 0 = Е 0· ε – начальные напряжения.
Рассмотренные математические модели явлений ползучести и релаксации описываются функциональной зависимостью, т.е. когда одному значению аргумента соответствует одно значение функции.
Вероятностная модель. В природе часто встречаются процессы, когда одному значению аргумента соответствует несколько значений функции, вследствие действия на явление случайных факторов. Рассмотрим модель вероятностного распределения сыпучего, вытекающего из бункера через сито в ящик с вертикальными перегородками (рис. 4.4).
Наблюдения показывают, что распределение сыпучего в ящике подчиняется нормальному закону, являющемуся математической моделью вероятностного процесса:
 |
, (4.6)
где y – ордината, количество песка в секции;
x – абсцисса, номер секции в ящике;
s – среднеквадратичное отклонение.
 |
Модель технологического процесса. В последнее время распространение получили модели, обеспечивающие оптимизацию технологических процессов. Рассмотрим так называемую транспортную задачу (рис. 4.5). Пусть имеется А 1, А 2, А 3 объектов строительства (шахтная поверхность, стволы), потребляющих соответственно а 1, а 2, а 3 количество щебня (а j, j = 3). В местах В 1 и В 2 есть карьеры с запасами щебня в 1 и в 2, (в i, i =2). При этом соблюдается условие а 1+ а 2+ а 3= в 1+ в 2.
Стоимость единицы продукции из карьера В 1 на объект А 1 равна С 11, на объект А 2 – С 12, на объект А 3 – С 13, т.е. [ C ij].
Количество щебня xij, транспортируемое на объект Аj из карьера Вi, взаимосвязано с другими величинами системой уравнений
(4.7)
В системе (4.7) первое уравнение означает количество щебня, транспортируемое из карьеров В 1 и В 2 на объект А 1; второе – на объект А 2; третье – на объект А 3. Четвертое уравнение означает количество щебня, доставляемое на объекты А 1, А 2, А 3 из карьера В 2 и т.д.
В этой системе, состоящей из 5 уравнений, имеется 6 неизвестных, поэтому задача имеет много решений. Требуется определить наиболее выгодный вариант (экономичный) перевозки щебня. В этом случае с помощью линейного программирования (численный метод) находят функцию, которая удовлетворяет условию
. (4.8)
Уравнения (4.7) и (4.8) представляют собой математическую модель, позволяющую оптимизировать транспортный поток. Схема решения задачи изображена на рис. 4.5.
 |
Кибернетическая модель. Интерес представляет кибернетическая модель «черного ящика» (рис. 4.6), описывающая систему неизвестной структуры и недоступной для непосредственного наблюдения. Известны лишь х i(вход), y i (выход),
(управляющие факторы), q n – (возмущающие факторы). Статистическим путем с помощью метода математического планирования эксперимента можно построить математическую модель исследуемого процесса. Модель отыскивается в виде уравнения регрессии, связывающего математическое ожидание случайной переменной у с контролируемыми величинами (x, z, q).
Модель-аналог. В теоретических и экспериментальных исследованиях, основываясь на аналогии, очень часто изучают явления на моделе-аналоге, а затем с помощью полученных зависимостей устанавливают закономерности в натуре.
На рис. 4.7 приведена простейшая электрическая модель-аналог для изучения напряженно-деформированного состояния балки на двух опорах. Реакции на опорах балки вычисляются из уравнений
(4.9)
по формулам:
; 
. (4.10)
Силу тока на входе и выходе электрической сети вычисляют аналогично:
; 
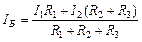. (4.11)
Таким образом, меняя силу тока І 1 и І 2 и сопротивление R, можно изучить реакции опор балки в зависимости от значения Р 1 и Р 2.
Модели-подобия. Используя модель подобия нет необходимости непосредственно, например, измерять высоту копра Н к, для этого достаточно использовать простейшую модель – треугольник и теорему о подобии треугольников. А высоту можно определить путем измерения расстояния к копру (рис. 4.8):
Н к = h · k р, (4.12)
 |
где k р – критерий подобия, равный k р = z / l.
Аналогичный прием используются и в более сложных моделях подобия. Однако при этом учитывается не только геометрическое подобие, но и кинематическое и механическое.
Имитационная модель. При решении задач о напряженно-деформированном состоянии пород вокруг выработки, когда математическую модель невозможно преобразовать к конечному виду, а упрощения приводят к грубым результатам, рационально использовать численные методы (например, метод конечных элементов), которые особенно эффективны в связи с применением вычислительных машин.
 |
|
ЛЕКЦИЯ 7