В научных исследованиях очень часто используют аналитические методы, которые позволяют установить математическую зависимость между параметрами изучаемого явления или процесса в явном виде, глубоко её проанализировать и установить точные количественные связи между аргументами и функциями.
Стремясь упростить исследуемую модель и получить простое решение поставленной задачи, широко применяют элементарные функции и уравнения, особенно линейные (y = аx, у = a + bx), например, прямолинейная огибающая кругов Мора. Для исследования процессов по принципу «ценного механизма» (разрушение, растворение, перемешивание и др.) используют экспоненциальные (у = е -х), параболические (у = х 2) и показательные (у = а х) функции. Чтобы изучить колебательные и периодические процессы применяют тригонометрические функции.
Элементарные функции непрерывны, что позволяет их дифференцировать и интегрировать, а также оптимизировать путем нахождения экстремумов. Например, производительность труда Р шахтостроительной организации зависит от годового объема работы V в виде:
Р = С 0 + С 1 V – C 2 V 2, (4.13)
где С 0, С 1 и С 2 – постоянные.
Анализ зависимости (4.13) показывает, что по мере увеличения объема работ производительность вначале возрастает, а затем убывает, так как в больших организациях сложно организовывать производство (рис. 4.10). Оптимальный объем работ для ШСУ можно найти, определив экстремум функции (4.13):
=0;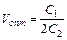 
. (4.14)
При анализе формы и размеров инженерных конструкций пользуются методами элементарной, начертательной и аналитической геометрий, а также векторным анализом.
Для теоретического анализа функций одной переменной используют дифференциальные уравнения. Уравнения первого порядка имеют вид:
– запись в неявном виде;
(4.15)
– запись в явном виде.
Часто применяют дифференциальные уравнения второго, третьего и более высших порядков:
. (4.16)
Общее решение таких уравнений представляет собой семейство кривых на плоскости. Кривая f (x, y) будет решением уравнения (4.15), если она в каждой точке касается вектора поля направления dy / dx. Поэтому каждое такое уравнение имеет множество решений (кривых):
F (x, y, C 1, C 2,…, C n) = 0, (4.17)
где С 1, С 2,…, С n – постоянные интегрирования.
Для нахождения частного решения необходимо задать начальные условия, число которых равно порядку уравнения. Это позволяет определить вначале постоянные С 1, С 2,…, С n, а затем и частные решения.
Обыкновенные дифференциальные уравнения применяются при решении задач о напряженном состоянии массива, равновесии конструкций, распределении масс, уплотнении грунтов, предельном состоянии пород и др.
Например, в результате исследований установлено, что после БВР скорость оседания пыли из движущегося по выработке воздуха пропорциональна ее количеству:
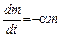, (4.18)
где m – количество пыли,
t – время;
α – коэффициент пропорциональности.
Преобразуем (4.18) к виду:
.
После интегрирования этого уравнения получим:
, 
;
При х = 0, m = m0, тогда С = ln m0., а искомая зависимость примет вид:
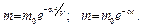(4.19)
По мере удаления от источника вследствие осаждения пыли концентрация ее будет уменьшаться по экспоненциальному закону.
Большое распространение при решении прикладных задач получили дифференциальные уравнения в частных производных, например,
, и др. (4.20)
Общее решение этих уравнений зависит уже не от произвольных постоянных, а от произвольных функций. В них искомые решения представляют собой функции нескольких независимых переменных. Суть решения задачи сводится к тому, чтобы найти соотношение между переменными, установить функциональные зависимости
u = f (x,y) или u = f (x, t),
удовлетворяющие дифференциальному уравнению с частными производными и частным условиям задач, которые называют краевыми условиями (начальными и граничными). Эти дополнительные условия определяются физическим смыслом задачи, они позволяют из множества решений получить одно, удовлетворяющее рассматриваемому процессу.
Условия, которые характеризуют все особенности искомого решения, называются условиями однозначности. Эти условия включают:
– геометрию системы (симметрия, форма и размеры тела);
– физические свойства тела (теплопроводность, водопроницаемость, упругость, пластичность, вязкость и пр.);
– начальные условия, т.е. состояние системы в начальный момент;
– граничные условия, т.е. взаимодействие системы на границах с окружающей средой.
Для решения линейных задач математической физики с простыми условиями, например, задачи тепломассообмена и им подобные, применяют операционные методы или методы интегрального преобразования Лапласа, Фурье, Бесселя и др. Суть операционного преобразования заключается в переводе функции f (t) переменного t, называемой начальной или оригиналом, в функцию f *(p) другого переменного р, называемую изображением. Далее изучают не саму функцию (оригинал), а ее измененное значение (изображение).
Преобразование осуществляется путем умножения начальной функции на другую и интегрирования ее. Так, преобразование Лапласа от функции f (t) имеет вид 
, где р – комплексное число.
Использование функции изображения f *(p) позволяет сложные операции дифференцирования и интегрирования f(t) заменить простыми алгебраическими операциями с f *(p). Выполнив эти операции, производят обратный переход к f (t).
При решении нелинейных задач со сложными краевыми условиями точные аналитические методы встречают значительные трудности.
Многие задачи исследуются с помощью вариационного исчисления. Для этого вводят понятие функционала. Пусть имеем кривую y = f (x) с областью определения x 0 ≤ x ≤ x 1 (рис. 4.11). Длина кривой L, площадь криволинейной трапеции F, объем тела вращения V зависит 
от вида заданной кривой:
(4.21)
Таким образом, функция y = f (x) однозначно определяет значения L, F и V, т.е. играет роль своеобразного «аргумента». В этом случае величины L, F, V называют функционалами относительно функции у = f (x). Суть задачи вариационного исчисления состоит в том, что, если задан функционал F (y ´) в области x 0 ≤ x ≤ x 1, то требуется найти такую функцию у = f (x), при которой этот функционал принимает экстремальные значения.
В фундаментальных исследованиях часто применяют тензорное исчисление. При этом изучаемая величина имеет определенный физический смысл и не зависит от выбора системы координат. Такие величины называются тензорами. Например, напряженное состояния пород в точке характеризуется тензором
.
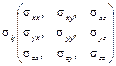Тензорное исчисление – раздел математики, изучающий тензоры и тензорные поля средствами линейной алгебры и математического анализа.
В теории упругости для определения концентраций напряжений в плоскости или пространстве, содержащей различные вырезы (выработки) широко используется теория функций комплексной переменной. В основе этой теории лежит положение о конформном преобразовании, когда изучение процессов в сложной области можно заменить более простым, отображая эту область на полуплоскость или круг. Функция комплексного переменного – функция, у которой независимая переменная Z и сама функция ω = f (Z) принимают значения из области комплексных чисел.
Рассмотренные аналитические методы, как правило, позволяют успешно решать только относительно простые задачи. В то же время часто возникает необходимость использования сложных дифуравнений или систем с нелинейными начальными и граничными условиями. В этом случае прибегают к тем или иным приближенным вычислениям с помощью численных методов (конечных разностей, конечных элементов). Эти методы основаны на замене непрерывного процесса изменения функции скачкообразным, что позволяет решать задачи на ЭВМ. Сводятся они к решению системы алгебраических уравнения с большим числом неизвестных, количество которых определяется разбивочной сеткой.