МАТРИЦА РАЗМЕРНОСТЕЙ ОСНОВНЫХ ПАРАМЕТРОВ, П-ТЕОРЕМА

Для использования алгебраического подхода к анализу размерностей удобно представлять размерности искомых величин и определяющих параметров данного класса явлений в форме таблиц. Каждый столбец таблицы состоит из показателей степеней, входящих в формулу размерностей (1.4) для одного из основных параметров. Число строк таблицы т равно количеству основных единиц измерения, число столбцов п — количеству основных параметров. Например, таблица размерностей для перечня основ­ных параметров (1.5) имеет вид

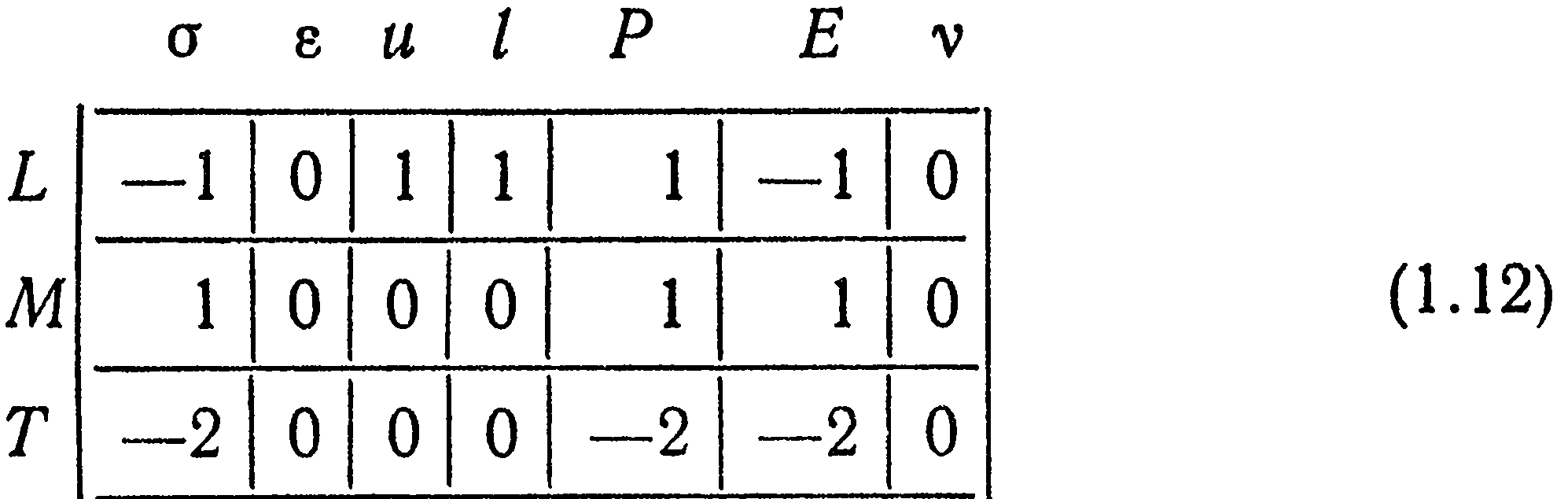
Прямоугольная таблица чисел (1.12) образует матрицу раз­мерностей основных параметров, обозначаемую двойными верти­кальными линиями:

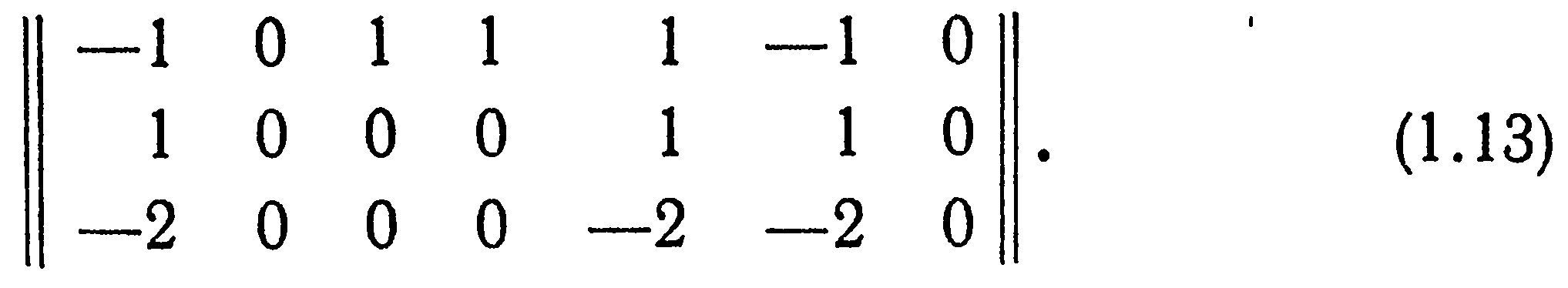
В общем случае для прямоугольной матрицы размером тxп, состоящей из элементов α_ij (i=1, 2,..., т;j=1,2,..., n), будем пользоваться обозначениями

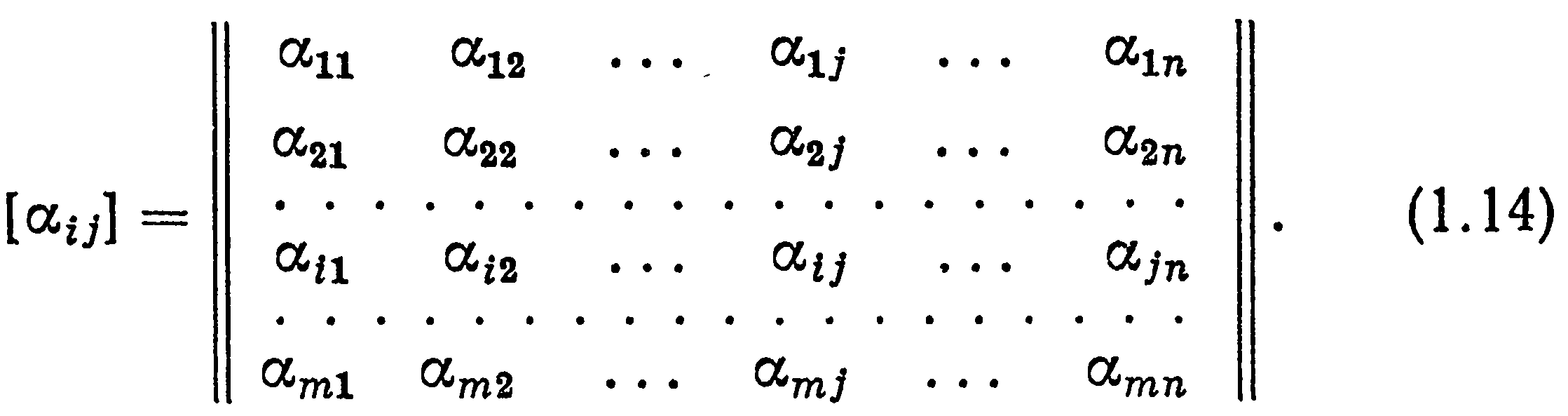
В матрице (1.14) всегда можно выделить k строк и k столбцов
(k≤т, k≤п) из элементов, стоящих на их пересечении и соста-
вить определитель k-го порядка. Все такие определители назы-
ваются минорами матрицы (1.14).

Минор второго порядка -63

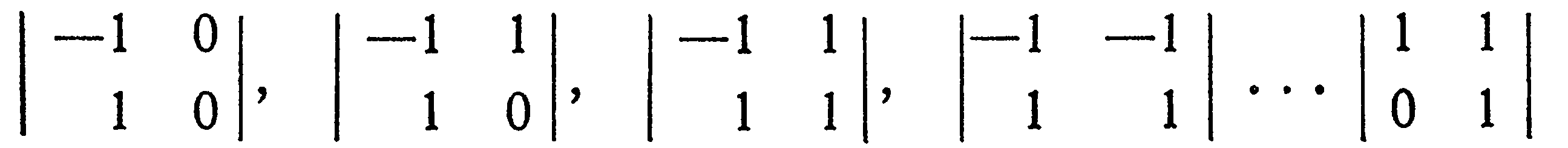
35 миноров третьего порядка

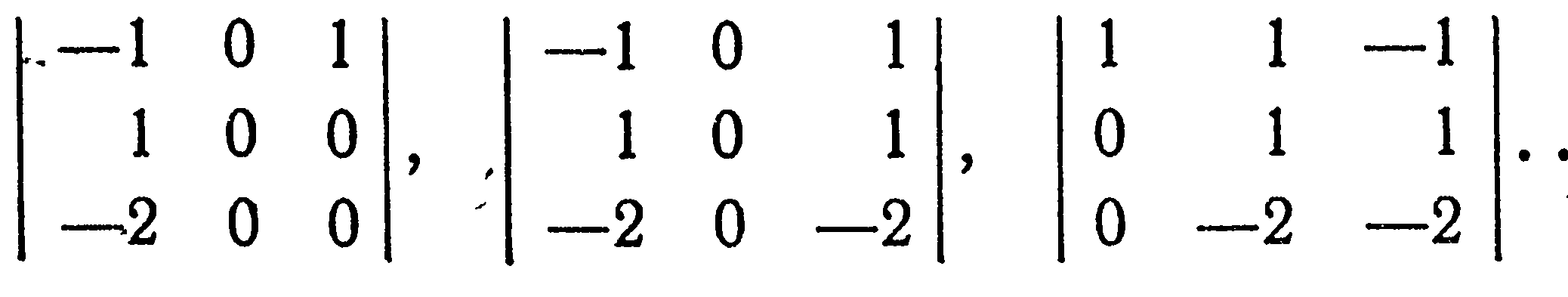
Среди миноров различных порядков некоторая их часть может быть равной нулю. Оставшиеся миноры вплоть до k-го порядка отличны от нуля.

Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. То есть если ранг матрицы равен r, то среди ее миноров есть, по крайней мере, один минор r-го по­рядка, отличный от нуля, в то время как все миноры порядка r + 1 и выше равны нулю. Ранг матрицы (1.14) обозначается r [α_ij].

В примере все миноры третьего порядка матрицы (1.13) равны нулю, а среди миноров второго порядка имеются опреде­лители, отличные от нуля. Таким образом, ранг матрицы раз­мерностей (1.13) r= 2.

Если какая-либо строка (столбец) матрицы (1.14) представляет собой линейную комбинацию двух или нескольких других, то система строк (столбцов) называется линейно зависимой.

Рангом системы строк (соответственно столбцов) матрицы называется наибольшее число линейно независимых среди них.

Одним из свойств прямоугольных матриц является равенство рангов ее строк и столбцов рангу матрицы [α_ij].

Для матриц размера тхп, когда значения тип достаточно велики, определение ранга rпутем вычисления миноров может оказаться неудобным. В этом случае ранг матрицы может быть найден с помощью операции приведения к каноническому виду.

Канонической матрицей называется матрица, у которой в на­чале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю, например

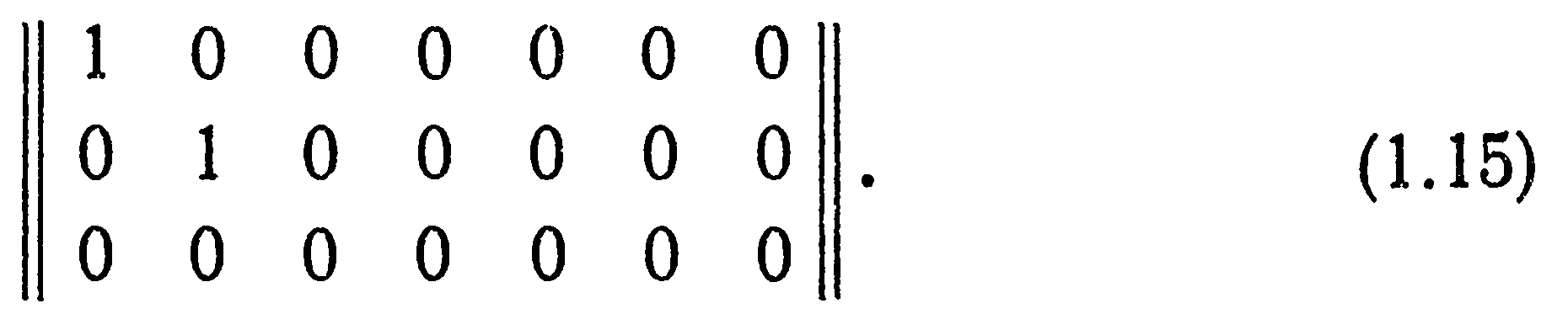
Любую матрицу при помощи элементарных преобразований строк и столбцов, заключающихся в перестановке строк (столб­цов), умножении строки (столбца) на число и сложении строк (столбцов) между собой, можно привести к каноническому виду. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Нетрудно убедиться, что путем элементарных преобразований рассмотренная выше матрица (1.13) приводится к каноническому виду (1.15), а ее ранг равен двум.

С понятием ранга матрицы связано, в частности, исследова­ние линейной независимости показателей размерностей физиче­ских величин, образующих безразмерные комбинации, и установ­ление количества независимых безразмерных комплексов, обра­зованных из заданного числа основных параметров.

В теории размерностей доказывается фундаментальная теорема — так называемая π-теорема, устанавливающая связь между числом основных параметров, количеством независимых безразмерных комплексов, образованных из основных параметров, и рангом матрицы размерностей.

π-теорема утверждает, что соотношение между искомыми величинами и определяющими параметрами (1.9) всегда может быть преобразовано к безразмерной форме, содержащей в качестве новых переменных безразмерные комбинации основных параметров. Количество независимых безразмерных комбинаций, об­разованных из определяющих параметров и искомых величин, равно разности между числом основных параметров и рангом матрицы размерностей.

При доказательстве сформулированной выше π -теоремы исхо­дят из следующих предположений [34]:

I) всякая величина Q_j (j —1,2,..., п) на основании формулы размерностей (1.4) и результатов § 1.2 может быть представлена в основных единицах базиса L_i (i = 1, 2,..., т):

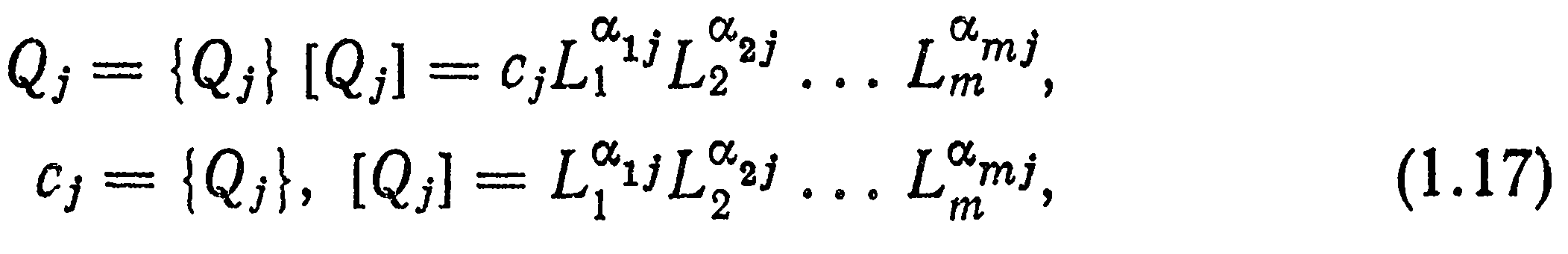
где α_ij — некоторые показатели степени; символами [ ] и { } обозначаются соответственно единицы измерения вторичных ве­личин, заключенных в скобки, и числовые значения этих величин;

II) любая безразмерная величина π (1.11), составленная из основных параметров Q_j, может быть представлена в виде произведения

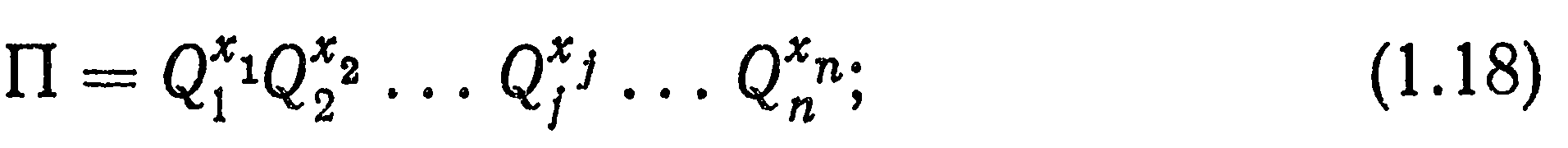
III) между основными единицами базиса L_i в силу их не­зависимости, не существует никаких других соотношений, кроме тождеств.

Первая часть π-теоремы утверждает, что функция F (1.16) может быть преобразована таким образом, что ее аргументами будут только безразмерные величины:

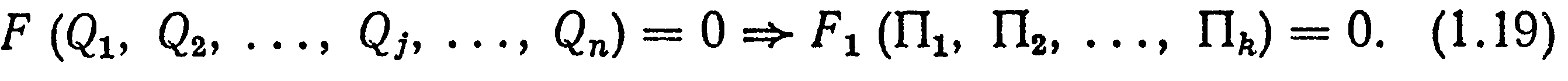
Вторая часть π-теоремы заключается в утверждении, что число безразмерных параметров π_k в уравнении F₁ = 0 (1.19) равно разности между количеством п основных параметров Q_jи рангом r матрицы размерностей:

Вывод - из неограниченного числа без­размерных комбинаций (1.18), которые могут быть образованы из п основных параметров Q_j, лишь только п —r значений яв­ляются независимыми. Они носят название фундаментальных безразмерных комплексов. Иными словами, в результате приве­дения функции п переменных F (Q₁, Q₂,..., Q_n) = 0 к безраз­мерному виду F₁ (π₁, π₂,..., π_n-r) = 0 число аргументов этой функции может быть уменьшено до чиcла п — r. В этом заключается наиболее существенный результат π -теоремы анализа размерностей.

Для случая r= т, то есть когда ранг матрицы размерностей равен числу основных единиц измерения, π -теорема была сфор­мулирована Фурье, Рябушинским и Рэлеем [74].