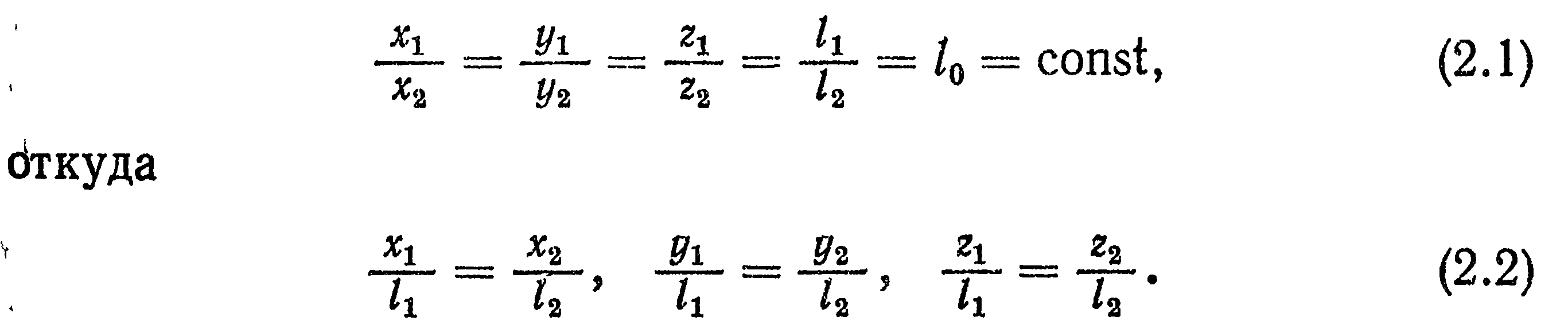ПРАКТИЧЕСКИЕ ПРИЕМЫ ПОЛУЧЕНИЯ

ФУНДАМЕНТАЛЬНЫХ СИСТЕМ БЕЗРАЗМЕРНЫХ КОМПЛЕКСОВ.

МАТРИЦА РЕШЕНИЙ

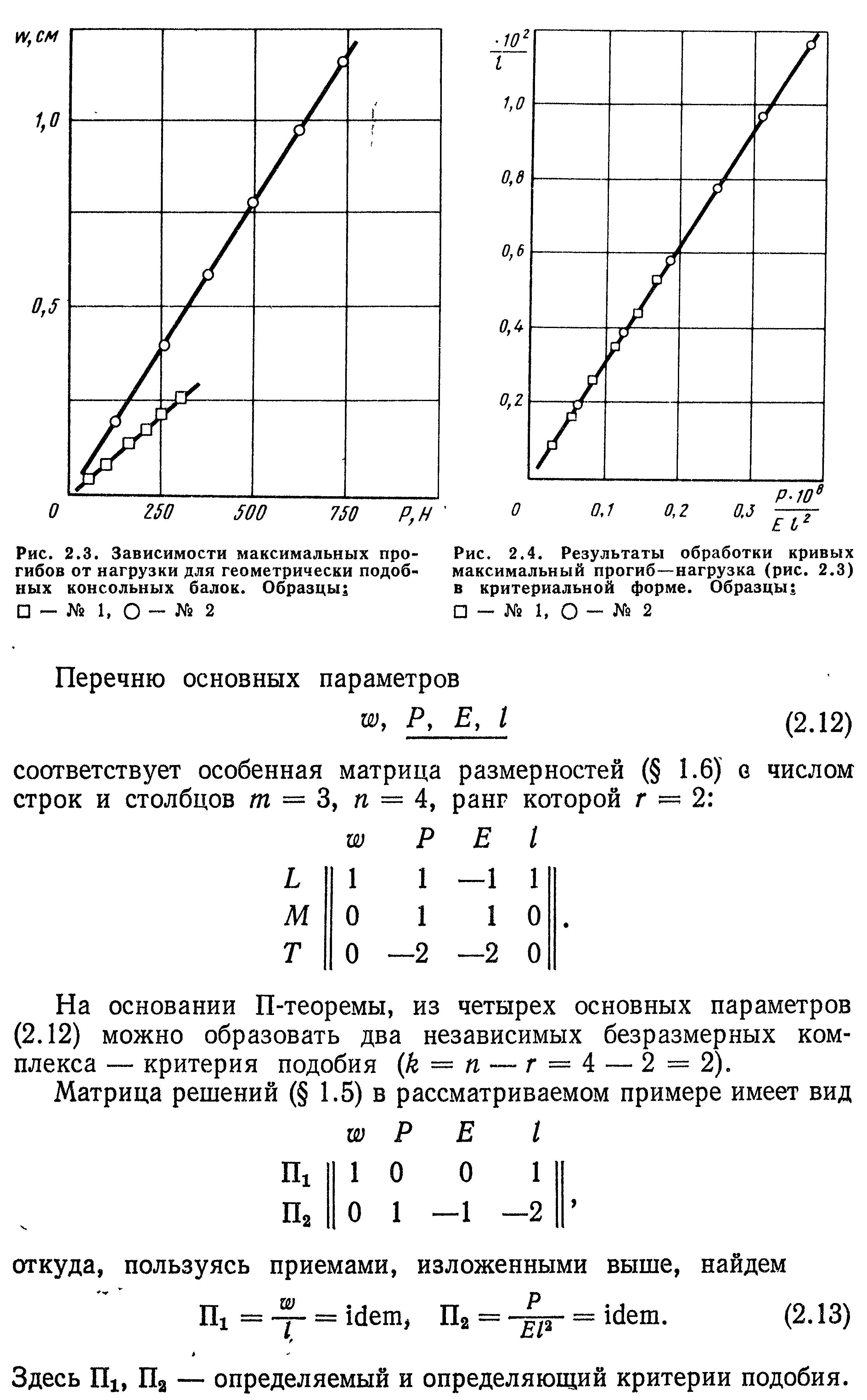
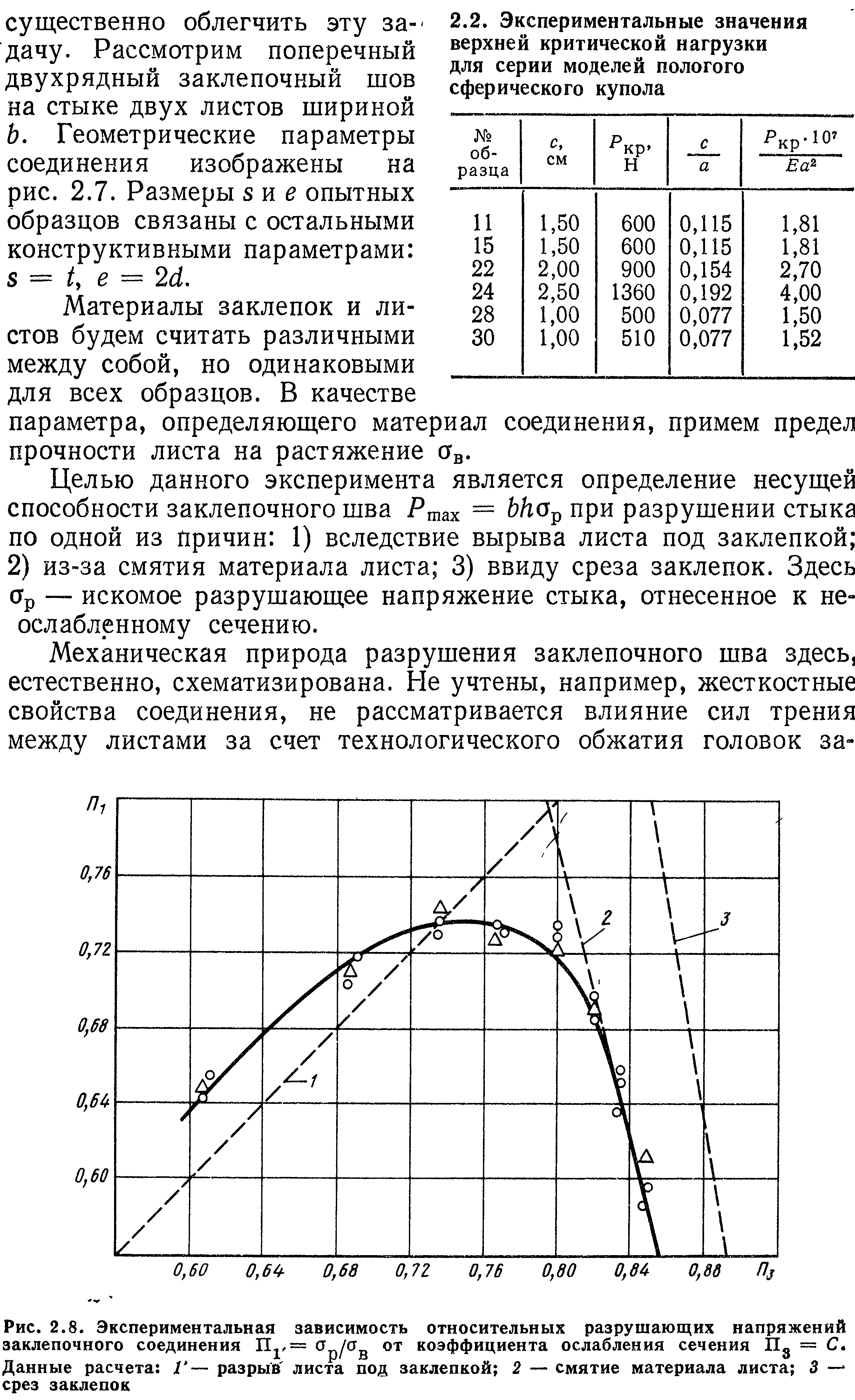
Рассмотрим перечень основных параметров (1.6), приве­денных в § 1.2 для задачи о динамическом нагружении упругого тела, и получим для этого случая систему независимых безраз­мерных комплексов.

В соответствии с предположением (1.18), положенным в основу π -теоремы анализа размерностей, будем искать общее выражение для неизвестного безразмерного отношения в форме

 

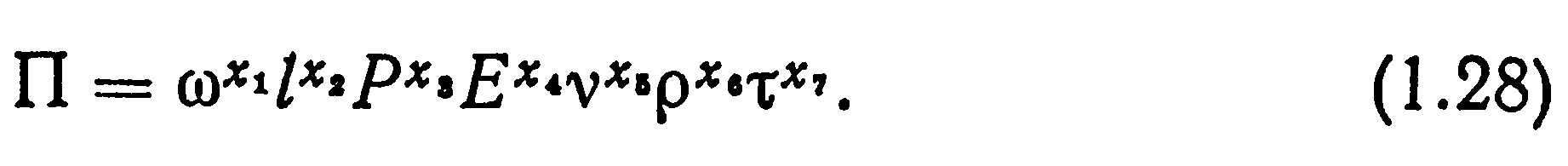
Здесь — показатели степени, подлежащие определе­нию. В число основных параметров с целью упрощения выкла­док включена лишь одна искомая величина — частота колеба­ний ω. Матрица размерностей в технической системе единиц МКГСС (см. табл. 1.1) о базисом L₁ (м), L₂ (кгс), L₃ (с) имеет вид

 

 

 

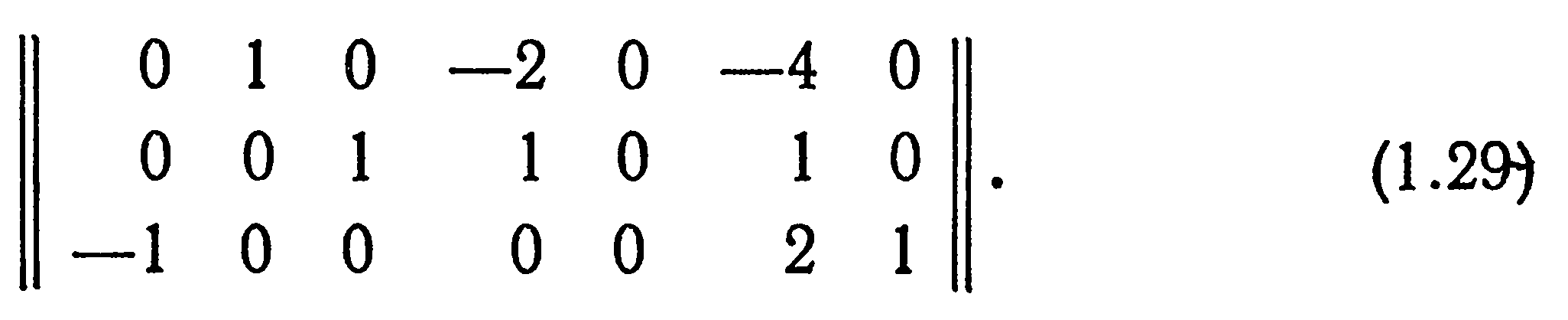
Пользуясь матрицей размерностей (1.29) и формулой размер­ности (1.4), подсчитаем размерность произведения (1.28):

 

\

 

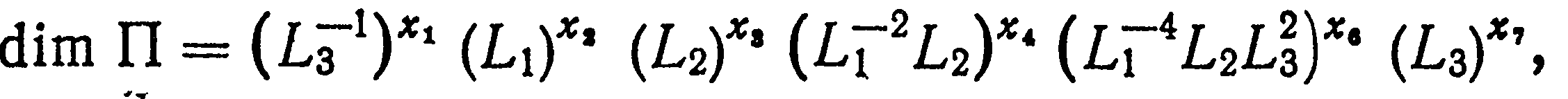откуда, учитывая свойства показательных функций, найдем

 

 

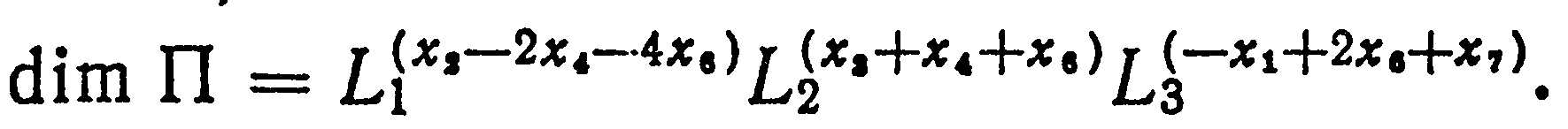
Условие безразмерноcти произведения π приводит к системе алгебраических уравнений для неизвестных показателей х_j:

 

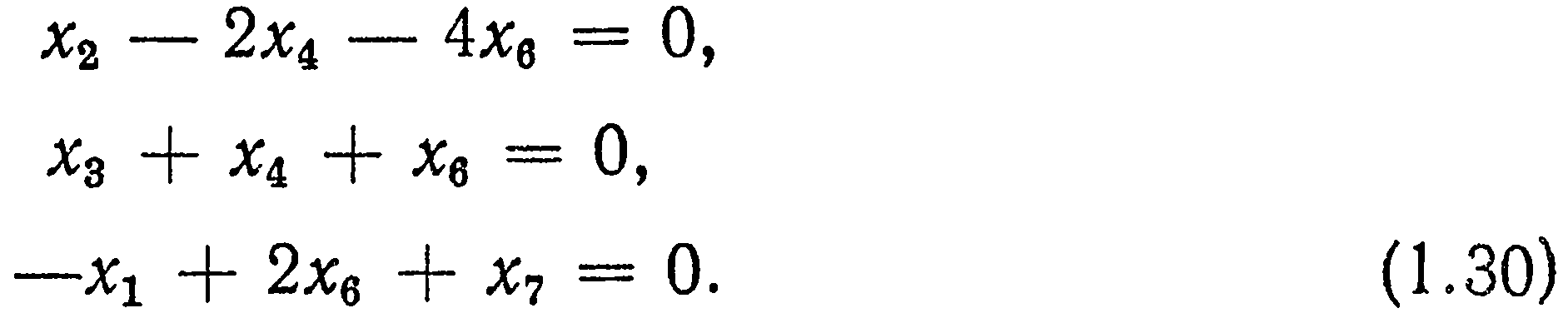
Любое решение системы линейных однородных уравнений (1.30) дает набор показателей степени для безразмерных комплек­сов π.

Анализ этой системы показывает, что числовые коэффициенты при неизвестных x_j каждого из уравнений представляют собой строки матрицы размерностей. Поэтому уравнения для показа­телей степени x_j безразмерного комплекса π могут быть написаны непосредственно, исходя из числовых значений элементов ма­трицы (1.29).

Особенностью системы (1.30) является отсутствие среди иско­мых показателей степени x_jнеизвестного х₅, что является след­ствием безразмерности коэффициента Пуассона ν. Поэтому ве­личина х₅ остается неопределенной и может принимать любые конечные числовые значения.

Система (1.30) содержит три уравнения с шестью неизвест­ными и, следовательно, имеет неограниченное число решений. Любое из них может быть выражено через три показателя степени, например через x₄, х₆ и x₇:

 

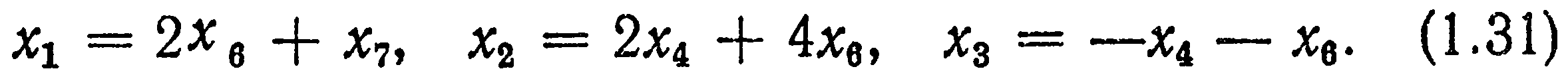
Ввиду того, что показатели x₄ х₅,х₆ и х₇ произвольны, будем последовательно полагать:

 

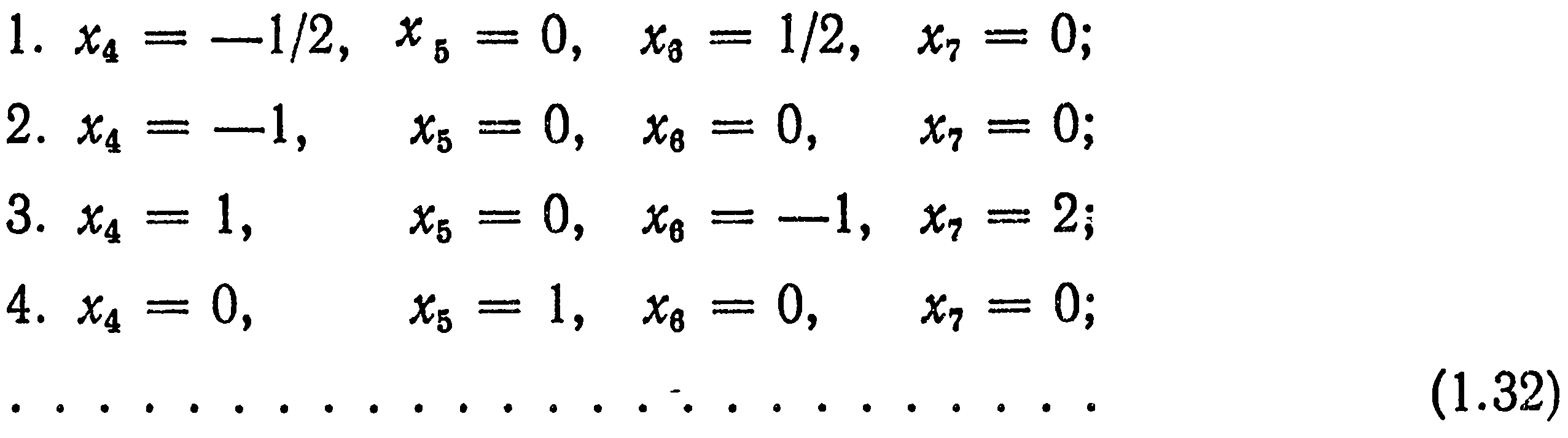
Остальные показатели степени Xj находят по формулам (1.31):

 

 

 

 

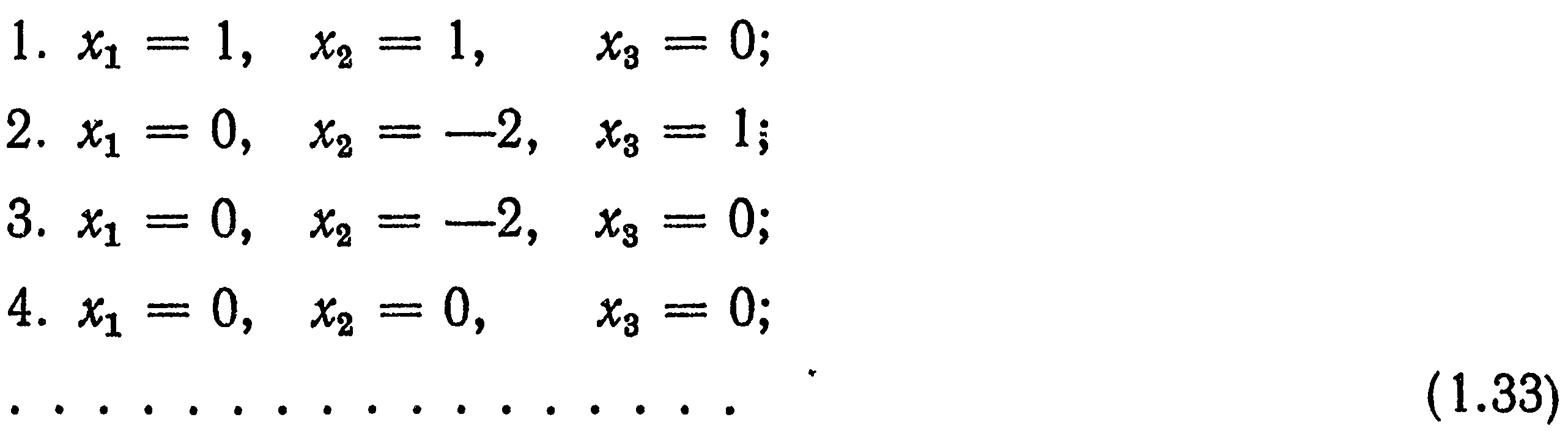
КЛАССИЧЕСКАЯ ТЕОРИЯ МЕХАНИЧЕСКОГО ПОДОБИЯ И МОДЕЛИРОВАНИЯ

 

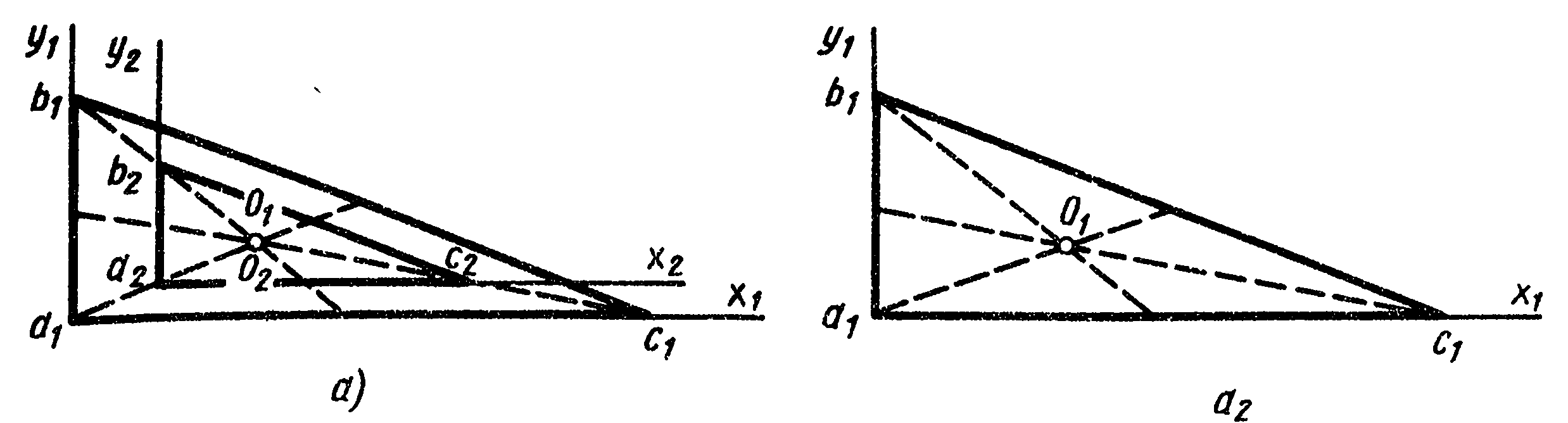
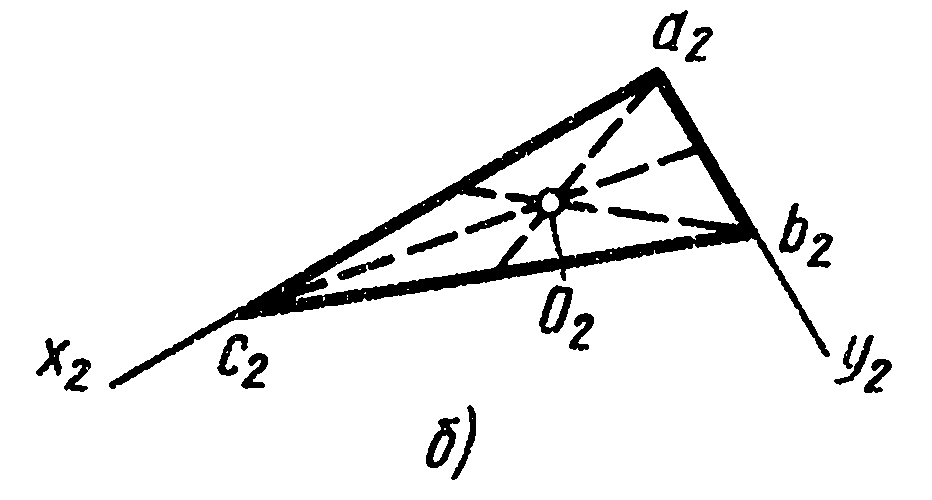
Рис. 2.1. Геометрически подобные плоcкие фигуры,сходственного (а) и несходственно (б) расположенные.

 

элементы (точки, линии, поверхности) при этом называютсясходствеными.

Очевидно, что две геометрически подобные фигуры, расположенные сходственным образом, можно путем поступательных перемещений и поворотов расположить совершенно произвольным образом одна относительно другой (рис. 2.1. Хотя в этом случае относительное расположение фигур в целом и не является сходственным, для соответственных элементов геометрически подобных фигур (точки а₁ и а₂, в₁ и в₂, линии b₁c₁ и в₂с₂ и т. п.) сохраняется понятие сходственных элементов,
Для каждой из сходственных точек геометрически подобных тел 1 и 2 справедливы соотношения