Описание случайной величины с помощью функции распределения 
является исчерпывающим, но для практических задач излишне подробным и не всегда удобным. Часто в приложениях бывает достаточно характеризовать свойства случайной величины посредством некоторого числа, т.е. перейти к числовым характеристикам.
Математическим ожиданием (средним значением) дискретной случайной величины 
называется величина
.
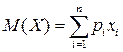Для непрерывной случайной величины, заданной плотностью распределения, математическое ожидание вычисляется как
.
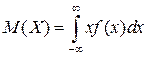Основные свойства математического ожидания:
· 
, где 
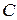- неслучайная величина;
· 
;
· 
;
· 
, если и 
некоррелированные случайные величины.
Математическое ожидание характеризует центр группирования значений случайной величины. Характеристикой рассеяния случайной величины относительно центра распределения служит дисперсия, определяемая как математическое ожидание квадрата отклонения случайной величины: 
, или, после преобразований 
. Для вычисления дисперсии в случае дискретной величины можно использовать, например, формулу
,
а в случае непрерывной случайной величины -
.
Основные свойства дисперсии:
· 
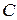, где - неслучайная величина;
· 
;
· 
, если и некоррелированные случайные величины.
Среднеквадратическое (стандартное) отклонение определяется как квадратный корень из дисперсии: 
.
Мерой взаимосвязи двух случайных величин и может служить коэффициент ковариации, численно равный величине
или, аналогично вычислению дисперсии,
.
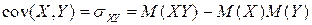Основным свойством коэффициента ковариации является равенство его нулю в случае независимости случайных величин и . (При этом обратное утверждение, вообще говоря, неверно!). Однако зависимость величины 
от масштаба измерения величин и делает неудобным его использование в практических приложениях. Поэтому в качестве меры связи признаков обычно используют другую числовую характеристику 
, называемую коэффициентом корреляции.
Следующие свойства коэффициента корреляции являются наиболее существенными:
· 
- абсолютное значение коэффициента корреляции не превосходит единицы;
· 
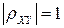только в том случае, когда случайные величины и связаны линейной зависимостью;
· если и - независимые величины, то 
. В этом случае говорят, что эти величины не коррелируют;
· величина инвариантна относительно линейных преобразований.
В случае многомерных случайных величин в рассмотрение вводятся соответствующие аналоги. Так, если 
, то вектором средних значений называют вектор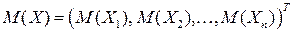 
, который является характеристикой центра группирования. В качестве меры рассеяния компонент и их взаимосвязи используется матрица ковариаций,
,
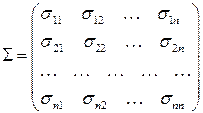элементы которой определяются равенством 
. Определитель этой матрицы 
называется обобщённой дисперсией. По причине, указанной выше, в практических приложениях предпочитают использовать матрицу, составленную из коэффициентов корреляции, 
, т.н. корреляционную матрицу. Аналогичным образом определяется взаимосвязь многомерных случайных величин и .