Таким образом, Z-преобразование взвешенной суммы двух последовательностей равно взвешенной сумме
Z-преобразований этих последовательностей.
2.Сдвиг последовательностей. Пусть последовательность yn представляет собой сдвинутую (задержанную) на m
отсчетов последовательность xn
.
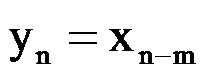Рассмотрим случай, когда все члены последовательности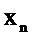 
с отрицательными индексами равны нулю
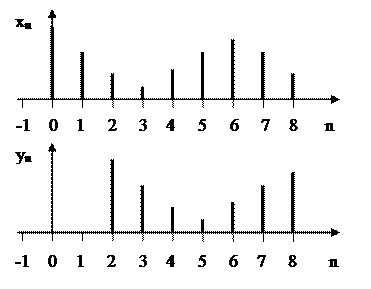
Рисунок 6 – Последовательность yn сдвинута относительно xn на 2 отсчета (2 интервала дискретизации)
Определим Z-преобразование последовательности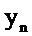 
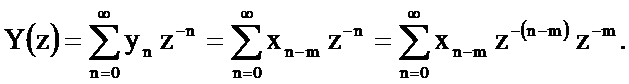
Обозначим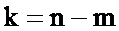 
и перепишем последнее соотношение
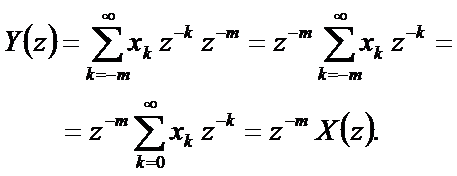
Тогда Z-преобразование Y(z) последовательности yn выражается через Z-преобразование X(z) последовательности xn следующим образом
.
Таким образом, Z-преобразование последовательности, задержанной относительно исходной на m отсчетов, равно Z-преобразованию исходной последовательности, умноженной на z –m.
3.Дискретная свертка двух последовательностей.
Дискретной сверткой двух последовательностей
xn и hn называется последовательность yn,
определяемая следующим соотношением
.
Определим Z-преобразование дискретной свёртки
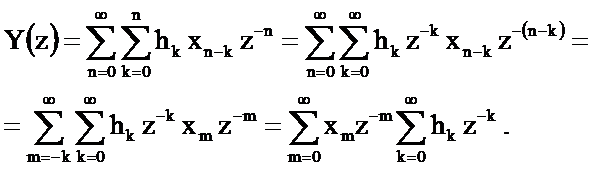
Поскольку при 
отсчёт последовательности 
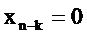, то внутренняя сумма не изменится, если её верхний предел n заменить на бесконечность.
Обозначим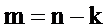 
, вынесем 
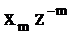за знак внутренней суммы и перейдём к суммированию по m, заменив нижний предел внешней суммы на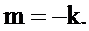 
Члены последовательности с отрицательными индексами равны нулю, следовательно, сумма от m = -k не отличается от суммы от m=0.
Полученное соотношение показывает, что
,
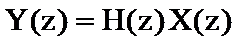где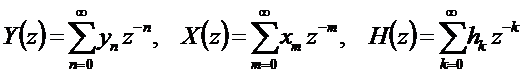 
.
Z-преобразование Y(z) дискретной свертки yn двух
последовательностей равно произведению Z –преобразований H(z) и X(z) исходных последовательностей hn и xn
2.2. Обратное Z-преобразование
Обратное Z-преобразование позволяет определить последовательность отсчётов дискретного сигнала по его прямому Z-преобразованию
Для определения обратного Z-преобразования найдём интеграл функции комплексного переменного 
, используя в качестве контура интегрирования 
окружность в плоскости комплексного переменного z с центром в начале координат и выражение для прямого Z-преобразования заменив в нём индекс суммирования n на k
В теории функций комплексного переменного доказывается, что интеграл от функции 
равен 
при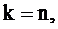 
при всех остальных значениях k он равен нулю. Поэтому из последнего соотношения получим
Если прямое Z-преобразование представлено полиномом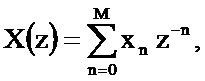 
где M-целое положительное число, то на основании определения прямого Z-преобразования n – ый член последовательности отсчётов дискретного сигнала xn является коэффициентом при 
Последовательность конечна, она содержит M+1 член.
Пример 1. Прямое Z-преобразование последовательности отсчетов xn определяется соотношением
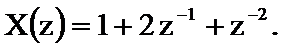
Требуется определить последовательность отсчётов дискретного сигнала
При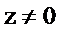 
первое слагаемое в выражении для
можно представить как 
, следовательно, 
. Коэффициенты при 
и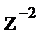 
2 и 1 соответственно. Поэтому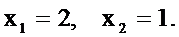 
Во всех других случаях для определения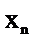 
нужно воспользоваться общим соотношением для обратного Z – преобразования.
Обозначим
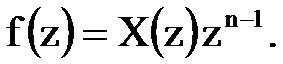
Функции комплексного переменного характеризуются полюсами и нулями.
Полюсом функции 
называется значение комплексного переменного z, при котором функция 
стремится к бесконечности.
Нулём функции 
называется значение комплексного переменного z, при котором функция 
равна нулю.
В теории функций комплексного переменного доказывается теорема о вычетах. Интеграл от функции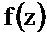 
, взятый по замкнутому контуру 
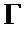, содержащемуся в области, где функция является однозначной и аналитической, за исключением особых точек однозначного характера, и не проходящему через особые точки, равен произведению суммы вычетов функции относительно всех особых точек, заключённых внутри , на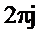 
.
Вычетом функции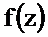 
относительно изолированной особой точки а однозначного характера называется коэффициент при 
в лорановском разложении функции в окрестности точки а.
Пусть а – простой полюс функции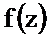 
. Тогда в окрестности точки а имеет место разложение в ряд Лорана
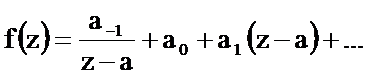
Умножим левую и правую часть последнего соотношения на 
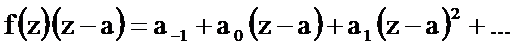
Из последнего соотношения следует
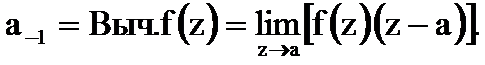
Вычисление вычета упрощается, если можно представить в виде отношения двух функций комплексного переменного
Функция 
имеет простой нуль при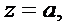 
т.е.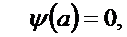 
Следовательно, 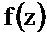имеет простой полюс при 
.
Найдём вычет 
Пример 2. Z-преобразование последовательности
определяется соотношением
Требуется найти последовательность xn
Подинтегральная функция 
определяется следующим соотношением
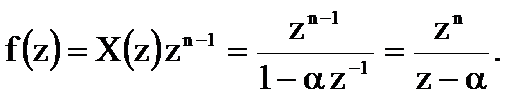
Из последнего соотношения следует, что
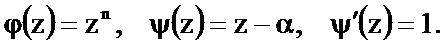
Нуль функции 
(полюс функции 
) находится из уравнения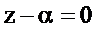 
и равен 
В результате получим
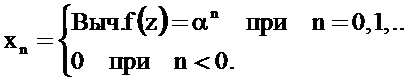
Если функция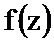 
имеет более одного полюса, то её нужно представить в виде суммы функций, имеющих только один полюс.
Пример 2. Z-преобразование последовательности 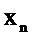определяется соотношением
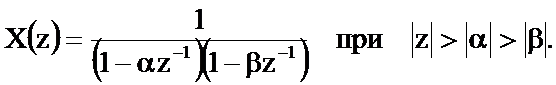
Требуется найти последовательность xn
Функция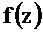 
определяется следующим соотношением
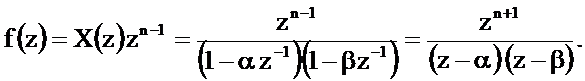
Преобразуем дробь, входящую в последнее соотношение
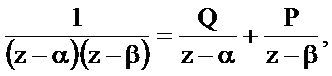
где Q и P – коэффициенты, которые следует определить.
Для определения коэффициента Q умножим левую и правую части последнего соотношения на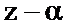 
и найдём пределы полученных выражений при 
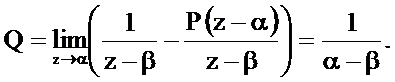
Для определения коэффициента P умножим левую и правую части уравнения на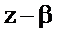 
и найдём их пределы при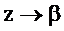 
Представим функцию 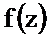с учётом соотношений для Q и P
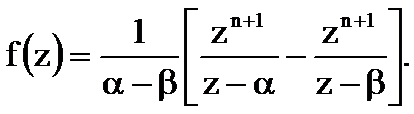
Определим последовательность отсчетов дискретного сигнала
Рассмотрим случай кратных полюсов. Пусть a – полюс кратности k. Тогда в окрестности точки a справедливо разложение в ряд Лорана
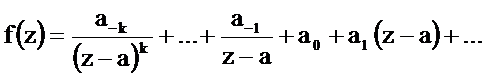
Умножим левую и правую части последнего соотношения на 
получим
Для определения a-1 продифференцируем последнее соотношение почленно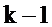 
раз
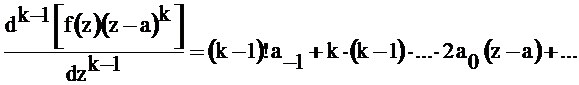
При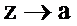 
получим
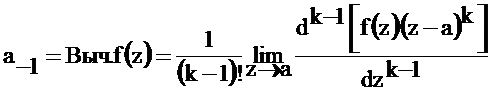. (2.10)
Пример 3. Z-преобразование последовательности 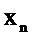определяется соотношением
Требуется найти последовательность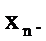 
Функция 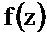определяется следующим соотношением
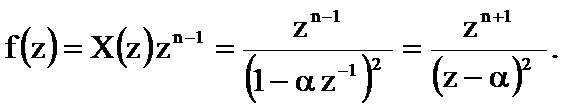
При k=2 найдем
2.3. Дискретные линейные системы, их свойства и характеристики
Системы обработки сигналов:
· Аналоговые,
· Дискретные,
· Цифровые.
Дискретные системы:
· Линейные,
· Нелинейные
Рисунок 1. Общее представление дискретной линейной системы