Рассмотрим разложения функций  ,
,  ,
,  в ряд Маклорена
в ряд Маклорена
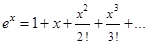 ,
,
 ,
,
 .
.
Положим  , тогда
, тогда
 .
.
Получили формулу

| (1.8) |
Равенство (1.8) называется формулой Эйлера.
С учетом этой формулы, комплексное число 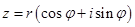 , записывается в форме,
, записывается в форме,
 , ,
| (1.9) |
которая называется показательной формой комплексного числа.
Пример 1.9
1)  , найти
, найти  .
.
Решение
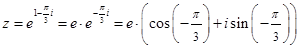 =
= 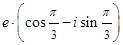 =
=
= 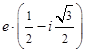 =
= 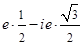
 .
.
Умножение, деление и возведение в целую положительную степень удобно производить, когда комплексное число записано в показательной форме.
1) 
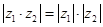 ,
, 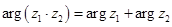 .
.
2) 
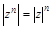 ,
, 
3) 
 ,
,  .
.
Рассмотрим операцию извлечения корня.
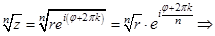
 ,
, 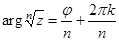 .
.
Из последних равенств следует формула извлечения корня из комплексного числа, представленного в тригонометрической форме:
 , ,
| (1.10) |
.
Приравнивая  числам 0,1, 2, …,
числам 0,1, 2, …,  получим
получим  значений корня.
значений корня.
Пример 1.10
Найти  .
.
Решение
 ,
, 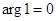

 .
.
Подставляя  , получаем три значения корня:
, получаем три значения корня:
 ,
, 
 ,
,  ;
;
 ,
, 
 |
Рис. 1.2
Тот факт, что комплексные числа  и
и  являются значениями корня третьей степени из единицы, означает, что
являются значениями корня третьей степени из единицы, означает, что 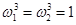 . Проверим,
. Проверим,  , используя алгебраическую форму числа
, используя алгебраическую форму числа  :
:
=  =
=  +
+
+  +
+ 
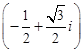 =
= 
 +
+
+  =
=  = 1.
= 1.
Здесь последнее произведение комплексных чисел является произведением комплексно сопряженных чисел и равно сумме квадратов действительной и мнимой частей 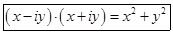 (см. пример 1.3).
(см. пример 1.3).
Пример 1.11
Вычислить  .
.
Решение
 .
.
Пример 1.12
Вычислить

Пример 1.13
Найти 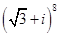 .
.
Решение
Воспользуемся тригонометрической формой числа  , полученной в примере 1.5:
, полученной в примере 1.5:  , тогда
, тогда  =
= 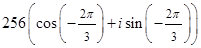 =
=  =
=  .
.
Понятие о функции комплексного переменного
Обозначим множество комплексных чисел С.
 . Пусть
. Пусть  и
и  . Если каждому комплексному числу
. Если каждому комплексному числу  по некоторому правилу поставлено в соответствие одно или несколько комплексных чисел
по некоторому правилу поставлено в соответствие одно или несколько комплексных чисел  , то говорят, что на множестве
, то говорят, что на множестве  задана функция
задана функция  .
.
Множество  называется областью определения, а множество
называется областью определения, а множество  областью значений функции
областью значений функции  . Если каждому значению z соответствует одно значение
. Если каждому значению z соответствует одно значение  , то функция называется однозначной, если несколько – функция многозначная.
, то функция называется однозначной, если несколько – функция многозначная.
Обозначая  , получим, что задание функции
, получим, что задание функции  комплексного переменного
комплексного переменного  равносильно заданию двух функций
равносильно заданию двух функций  и
и  двух действительных переменных x и y. Следовательно,
двух действительных переменных x и y. Следовательно,  , где
, где  ,
,  = =
= =  .
.
Пример 1.14
Для данной функции  , где
, где  , найти действительную часть
, найти действительную часть  и мнимую часть
и мнимую часть  :
:  .
.
Решение

т.е.  ;
;  .
.
Пример 1.15
Какая линия описывается уравнением  ?
?
Решение
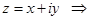

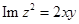 . Подставляя это выражение в заданное уравнение, получаем
. Подставляя это выражение в заданное уравнение, получаем  – уравнение гиперболы.
– уравнение гиперболы.
Задачи для самостоятельного решения
Для данных функций найти их действительную часть  и мнимую часть
и мнимую часть  :
:
1)  ; 2)
; 2) 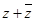 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6) 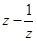 .
.
Ответы: 1)  ,
, 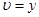 ; 2)
; 2)  ,
,  ; 3)
; 3)  ,
,  ; 4)
; 4)  ,
,  ; 5)
; 5)  ,
,  ;
;
6)  ,
, 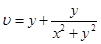 .
.
Основные элементарные функции
Комплексной переменной
Показательная функция 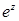 . По определению,
. По определению,
 . .
| (1.11) |


Можно показать, что при таком определении выполняются все обычные свойства показательной функции, например
 ,
, 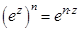 .
.
Покажем, что показательная функция (1.11) является периодической с периодом  :
:
 ,
,  .
.
Тригонометрические функции. По определению,
 ; ;  ; ;  ; ;
 . .
| (1.12) |
Можно показать, что при таком определении выполняются все известные формулы для тригонометрических функций, например,
 ,
,  ,
,  , и т.д.
, и т.д.
Пример 1.16
Решить уравнение:  .
.
Решение
 , в это уравнение подставим выражение (1.5) для синуса, получим
, в это уравнение подставим выражение (1.5) для синуса, получим 



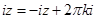

 ,
,  , где
, где  .
.
Гиперболические функции. По определению,
 , ,  , ,  , , 
| (1.13) |
Заменим в этих определениях z на  , тогда получим
, тогда получим
 ,
,  .
.
Таким образом,
 , , 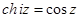
| (1.14) |
Если в формулах (1.8) заменить z на 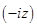 , то получим
, то получим
 , , 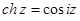 . .
| (1.15) |
Пример 1.17
Найти  .
.
Решение
Из второго соотношения (1.14) следует, что
 .
.
Пример 1.18
Найти  .
.
Решение
Из первого соотношения (1.15) следует, что
 .
.