Свойства равнобедренной трапеции
1.Боковые стороны равны.
2.Углы, прилежащие к основаниям равны (два острых и два тупых)
3. Сумма углов, прилежащих к боковой стороне равна 1800
4.Бисектрисы углов, прилежащих к боковой стороне, пересекаются под прямым углом
5. Длина средней линии трапеции равна большему отрезку на большем основании, если провести одну высоту
6. При решении задач всегда проводят две высоты. (равные отрезки на большем основании)
7. Средняя линия трапеции параллельна ее основаниям и равна 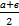 (полусумме оснований – параллельных сторон.)
(полусумме оснований – параллельных сторон.)
8.При решении задач. Если диагонали трапеции перпендикулярны, тогда вторую диагональ перенести параллельно к первой. Получим прямоугольный треугольник, гипотенуза = сумме оснований
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон.
Средняя линия треугольника параллельна одной из сторон и равна ее половине.
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.
Гипотенуза = 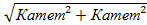 Катет =
Катет =  Гипотенуза больше катета.
Гипотенуза больше катета.
Как определить вид треугольника по углам
Большая сторона2 = сторона2 + сторона2 - треугольник прямоугольный
Большая сторона2 < сторона2 + сторона2 - треугольник остроугольный
Большая сторона2 > сторона2 + сторона2 - треугольник тупоугольный
сИнус острого угла прямоугольного треугольника равен отношению прО тиволежащего катета к гипотенузе 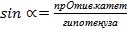
кОсинус острого угла прямоугольного треугольника равен отношению прИ лежащего катета к гипотенузе 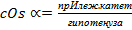
Тангенс острого угла прямоугольного треугольника равен отношению про тиволежащего катета к при лежащему катету 
Котангенс острого угла прямоугольного треугольника равен отношению при лежащего к атета к про тиволежащему катету 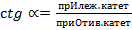
Сумма углов выпуклого многоугольника равна Sn = 1800 (n – 2), где n – количество сторон или углов. Сумма углов правильного многоугольника S = 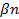 ,
, 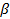 - угол многоугольника, n – количество сторон или углов
- угол многоугольника, n – количество сторон или углов
Сумма углов четырехугольника 3600
Сумма внешних углов многоугольника, взятых по одному при каждой вершине равна 3600.
В прямоугольном треугольнике высота проведена к гипотенузе, тогда
1. Высота, проведенная к гипотенузе = 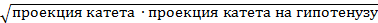
2. Катет = 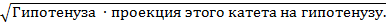
Медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины.
· Одна медиана разбивает треугольник на два треугольника равной площади. 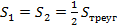
· Три медианы разбивают треугольник на 6 треугольников с равными площадями 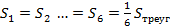
· Медиана, проведенная к гипотенузе прямоугольного треугольника, является радиусом описанной окружности R и равна половине гипотенузы
Подобие треугольников
· Периметры подобных треугольников пропорциональны коэффициенту подобия. 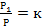
· Площади подобных треугольников пропорциональны квадрату коэффициенту подобия 
Признаки подобия
1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами равны, то такие треугольники подобны.
3. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Площадь треугольника:
1. Площадь треугольника равна половине произведения стороны на высоту, опущенную к ней. 
2. Площадь треугольника равна половине произведения двух сторон на синус угла между ними 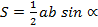
3. Площадь треугольника равна произведению полупериметра на радиус вписанной окружности 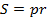 . (Для любого многоугольника)
. (Для любого многоугольника)
4. 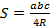 Площадь треугольника равна произведение трех сторон деленное на 4 радиуса описанной окружности R.
Площадь треугольника равна произведение трех сторон деленное на 4 радиуса описанной окружности R.
5. 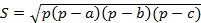 – формула Герона, p - полупериметр
– формула Герона, p - полупериметр
6. 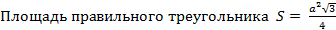
7. Площадь прямоугольного треугольника равна половине произведения катетов 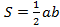
Площадь параллелограмма, ромба
1. Площадь параллелограмма равна произведению стороны на высоту, опущенную к ней. 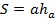
2. Площадь параллелограмма равна произведению двух сторон на синус угла между ними
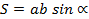
3. Площадь параллелограмма равна половине произведению диагоналей на синус угла между ними 
 (для любого четырехугольника)
(для любого четырехугольника)
4. Площадь ромба равна половине произведению диагоналей 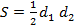 (для любого четырехугольника, у которого диагонали перпендикулярны)
(для любого четырехугольника, у которого диагонали перпендикулярны)
Площадь квадрата
1. Площадь квадрата равна стороне в квадрате S = a2
2. Площадь квадрата равна 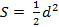
Площадь прямоугольника:
1. Площадь прямоугольника равна произведению смежных сторон. 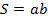
2. Площадь прямоугольника равна половине произведению диагоналей на синус угла между ними 
 (для любого четырехугольника)
(для любого четырехугольника)
Площадь трапеции
1. Площадь трапеции равна произведению полусумме оснований на высоту 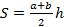
2. Площадь трапеции равна произведению средней линии на высоту 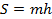
3. Если в трапеции диагонали перпендикулярны, то ее площадь равна 