Функция распределения случайной величины Х, распределенной по равномерному закону, есть
F(x) 
Её математическое ожидание:
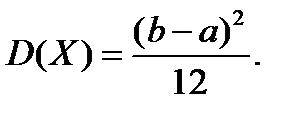
И дисперсия:
Равномерный закон распределения
Непрерывная случайная величина X имеет равномерный законраспределения на отрезке [a, b], если её плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.e.
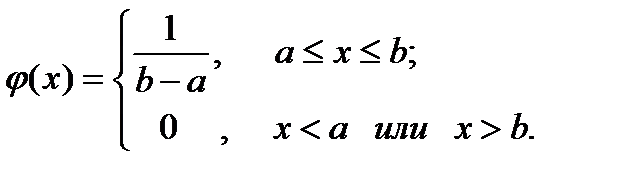
12 Биномиальный закон распределения вероятностей и его характеристики.Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения 0,1, 2,…,m,….,n с вероятностями р(m) = Р(Х = m) = Cnm рmqn-m, где 0 <p<1, q = 1─ р. Биномиальный закон распределения представляет собой закон распределения числа Х = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, даются формулами M(X) = np, D(X) = npq.Следствие. Математическое ожидание величины (m/n) в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. M(m/n) = р, D(m /n)=pq/n.
13.Закон распределения вероятностей Пуассона и его характеристики.Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0,1 2,…,m,…,n с вероятностями р(m) = Р(Х=m) =е─λ λm/m!, где λ = np.Tеорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона. М(Х) = λ, D(X)= λ. Распределение Пуассона ─ частный случай биномиального закона распределения для относительно больших n и относительно малых р.
|
|
14.Нормальный закон распределения вероятностей и его характеристики. Нормальный закон распределения вероятностей. Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и s2, если её плотность вероятности имеет вид:
Кривую нормального закона распределения, называют гауссовой кривой.
Теорема 1. Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а дисперсия - параметру s2, т. е. М(Х) = a, D(X)= s2.
Функция распределении случайной величины X, распределённой по нормальному закону имеет вид:
В частном случае, когда а=0, а s2=1 нормальное распределение называется стандартным.
Теорема 2. Функция распределении случайной величины X, распределённой по стандартному нормальному закону, выражается через функцию Лапласа Ф0(х) по формуле
где:
В общем случае
Свойства нормального распределения
1. Вероятность попадания случайной величины X, распределённой по нормальному закону, в интервал [х1, х2], равна
2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания a не превысит величину D> 0, равно:
Р(½Х -а½£D) = 2Ф0 (t), t = Ds.
По этой формуле можно рассчитать вероятности Р(½Х -а½£D), для различных значений D:
D = s, Р(½Х -а½£D) = 2Ф(1)=0,6827;
D = 2s, Р(½Х -а½£D) = 2Ф(2)=0,9545;
D = 3s, Р(½Х -а½£D) = 2Ф(3)=0,9973.
15.Экспоненциальный закон распределения вероятностей. Функция надежности.
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
|
|
функция распределения вероятностей имеет вид:
Вероятность попадания случайной величины в интервал (а;в) находится по формуле:
P (a<X<b) = 
- 
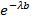
Для показательного распределения:
M(X)= 1/λ
D(X)= 1/ 
σ(X) = 1/λ
Ф-ция надежности
Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению
R(T) = P(T>t) – вероятность безотказной работы некоторого устройства за время t:
Показательный закон надежности – R(T)= 
,λ-интенсивность отказов. Функция R(T)называется функцией надежности
16.Центральная предельная теорема. Теорема Ляпунова.Теорема Ляпунова (центральная предельная теорема).Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.Пусть Х1,Х2,….Хn – независимые случайные величины, имеющие М(Х)=а и D(X)=σ2.Тогда для любого числа х верно:
17. Задачи математической статистики.Предмет и задачи матем.статистики. Составляет разработка методов регистрации описания и анализа статистич. Эксперементных данных получаемых в результате наблюдения массовых случайных явлений.Под статистическими данными понимается некоторая совокупность чисел, представляющих собой количественные характеристики изучаемых процессов и явлений.Задачиматемстатистики:Установление закономерностей, которым подчинены массовые случайные явления, изучение методами теории вероятностей статистических данных- результатов наблюдений.1-я задача: Указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально проведенных экпериментов.2-я задача: Разработать методы анализа статистич.данных в зависимости от целей исследованияА)Оценка неизвестной вероятности события: оценка неизвестной функции распределения оценка параметров распределения, вид которого известен, оценка зависимости случайной величины от одной или нескольких случайных величин.Б) Проверка статистич.гипотез о виде неизвестного распределения, вид которого известен.Современ. Матем.статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента) в ходе исследования (последовательный анализ) Современ.Мат.статистику определяют как науку о принятии решений в условиях неопределенности.Задача математической статистики состоит в создании методов отбора и обработки данных для получения научных и политических выводов.
|
|
18. Способы отбора данных. Генеральная и выборочная совокупность.
Генеральной совокупностью называется множество числовых значений рассматриваемой количественной характеристики всех исследуемых объектов. Выборочной совокупностью (или просто выборкой) называется множество числовых значений рассматриваемой количественной характеристики для объектов, случайным образом отобранных из всей совокупности рассматриваемых объектов. Объем совокупности (выборочной или генеральной) называют число объектов этой совокупности. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующим признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли, т.е. выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируется так: выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществлять случайно. Для этого существуют различные виды отбора выборки.На практике применяют различные способы отбора выбора.1. Отбор, не требующий разделения генеральной совокупности на части.а)простой случайный бесповторный отбор; б) простой случайный повторный отбор.
2.Отбор, при котором генеральная совокупность разбивается на части. а) типический отбор;б) механический отбор; в) серийный отбор.
19. Статистическое оценивание параметров дискретных случайных величин. Выборочная средняя и выборочная дисперсия.Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.Оценки параметров генеральной совокупности, полученные на основании выборки, называются статистическими. Если статистическая оценка характеризуется одним числом, то она называется точечной. Если статистическая оценка характеризуется двумя числами – концами интервала, то она называется интервальной.
К числу точеных оценок относятся выборочная средняя и выборочная дисперсия
Выборочная средняя определяется как среднее арифметическое полученных по выборке значений.
где
xi – варианта выборки;
ni – частота варианты;
n- объем выборки.
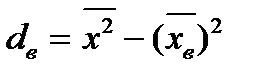
Выборочная средняя является оценкой математического ожидания случайной величины и представляет собой несмещенную оценку.Выборочная дисперсия представляет собой среднюю арифметическую квадратов отклонений вариант от их выборочной средней
.Удобно использовать формулу:
где - выборочная средняя квадратов вариант выборки.
Выборочная дисперсия оценивает дисперсию генеральной совокупности, является смещенной оценкой. Для устранения смещения вычисляют
s2называют несмещенной выборочной дисперсией.
21. Статистическое оценивание: метод моментов, метод максимального правдоподобия. Метод максимального правдоподобияМетод предложен Р. Фишером в 1912 г. Метод основан на исследовании вероятности получения выборки наблюдений (x1, x2, …, xn). Эта вероятность равна f(х1, T) f(х2,T) … f(хп, T) dx1 dx2 … dxn.Метод опирается на использование условий экстремума ф-ии одной или нескольких переменных. В качестве такой ф-ии принимают ф-ю правдоподобия. Метод моментовМетод предложен К. Пирсоном в 1894 г. Сущность метода: достаточно часто на практике при заданном виде закона распределения случайной величины Х можно оценить неизвестные параметры этого распределения. Сделать это можно несколькими способами. Доказано, что начальные и центральные эмпирические моменты являются самостоятельными оценками соответственно начальных и центральных теоритич. Моментов того же порядка. На этом основан метод моментов. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов, рассматриваемого распределения, соответствует эмпирическим моментам того же порядка. В случае одного параметра в теоретическом распределении.
22.Интервальные оценки для параметров нормального закона распределения.Интервальный метод оценивания параметров распределения случайных величин заключается в определении интервала (а не единичного значения), в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра. Интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра Т, получила название методов интервального оценивания. К их числу принадлежит метод Неймана.Постановка задачи интервальной оценки параметров заключается в следующем Имеется: выборка наблюдений (x1, x2, …, xn) за случайной величиной Х. Объем выборки n фиксирован.Необходимо с доверительной вероятностью = 1– определить интервал t0 – t1 (t0 < t1), который накрывает истинное значение неизвестного скалярного параметра Т(здесь, как и ранее, величина Т является постоянной, поэтому некорректно говорить, что значение Т попадает в заданный интервал).Ограничения: выборка представительная, ее объем достаточен для оценки границ интервала.Эта задача решается путем построения доверительного утверждения, которое состоит в том, что интервал от t0 до t1 накрывает истинное значение параметра Т с доверительной вероятностью не менее . Величины t0 и t1 называются нижней и верхней доверительными границами (НДГ и ВДГ соответственно). Доверительные границы интервала выбирают так, чтобы выполнялось условие P(t0 t1) = На практике применяют два варианта задания доверительных границ:устанавливают симметрично относительно оценки параметра, т.е. t0 = – Е, t1 = + Е, где Е выбирают так, чтобы выполнялось доверительное утверждение. Следовательно, величина абсолютной погрешности оценивания Е равна половине доверительного интервала;устанавливают из условия равенства вероятностей выхода за верхнюю и нижнюю границу Р(Т > + Е1,)=Р(Т < – Е2,)= /2. В общем случае величина Е1, не равнаЕ2,. Для симметричных распределений случайного параметра в целях минимизации величины интервала значения Е1, и Е2, выбирают одинаковыми, следовательно, в таких случаях оба варианта эквивалентны.Нахождение доверительных интервалов требует знания вида и параметров закона распределения случайной величины . Для ряда практически важных случаев этот закон можно определить из теоретических соображений.
23. Статистические оценки параметров распределения. Несмещенность, состоятельность, эффективность и надежность оценки.Статистические оценки должны отвечать определенным требованиям, чтобы соответствовать оцениваемым параметрам, т.е. иметь близкие к ним значения.Этитребования:несмещенность– математическое ожидание оценки должно равняться оцениваемому параметру эффективность- оценка при заданном объеме выборки должна обеспечивать наименьшую дисперсию состоятельность – по мере увеличения объема выборки оценка должна сходиться по вероятности к оцениваемому параметру т.е
Достоверной вероятностью (надежностью) оценки параметра называется вероятность β, с которой осуществляется неравенство
, где δ положительной число, характеризующее точность оценки.
В качестве величины β принимают число близкое к единице (обычно β имеет значения 0,90; 0,95; 0,99).
Соотношение
определяет вероятность того, что неизвестный параметр с доверительной вероятностью β находится в пределах доверительного интервала.
24. Статистическая гипотеза. Нулевая гипотеза. Ошибки первого и второго рода.
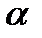Статистической называют гипотезу о виде неизвестного распределения или о параметра х известных распределений.
Гипотеза о том, что две совокупности, сравниваемые по одному или нескольким параметрам не отличаются считается нулевой гипотезой.
Нулевой гипотезой (основной)называют выдвинутую гипотезу Н0. Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.
Поскольку проверку проводят статистическими методами, то её называют статистической.
В итоге статистической проверки гипотезы могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода равна уровню значимости.
Ошибка второго рода - гипотеза Н0 принимается, а на самом деле она неверна.. Вероятность ошибки второго рода равна β.
Соответственно тогда вероятность принять верную гипотезу равна
а вероятность отвергнуть неверную гипотезу равна 1- β.
25 .Проверка статистической гипотезы о равенстве средних значений.
Проверяем гипотезу Н0: ах=ау,
альтернативная гипотеза н1 может быть трех видов.
а) ах≠ ау;
б) ах>ау;
в) ах<ау.
Однако случай в) сводится к б) перестановкой х и у и не будет рассматриваться отдельно.вычисляют статистику критерия:
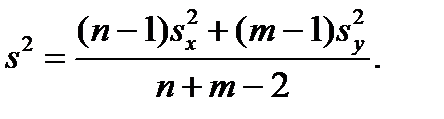где
величина s2 является объединенной оценкой дисперсии (общей для выборок).формулу можно представить в виде Для проверки берутся критические точки tкр распределения Стьюдента с n+m-2степенями свободы и уровнем значимости α, причем в случае а) - для двусторонней критической области, в случае б) – для односторонней критической области.В случае а) если IT I <tкр, гипотеза Н0 принимается, если IT I >tкр – отвергается.В случае б)если T<tкр, то гипотеза Н0 принимается, если T>tкр – гипотеза Н0 отвергается.
Замечание. Поскольку для проверки гипотезы требуетсяравенстводисперсий у двух выборок, сначала необходимо проверить гипотезу о равенстве дисперсий. В противном случае метод применять нельзя.
26. Проверка статистической гипотезы об однородности дисперсий.
Предположим, что известныисправленные выборочные дисперсии для обеих выборок – sx2 и sy2.
Проверяем гипотезу Н0: σх2= σy2.
Альтернативная гипотеза Н1может бытьтрехвидов:
а) σх2≠ σy2
б) σх2> σy2
в) σх2< σy2.
Однако случай в)сводитсяк б) перестановкой х и у и не будет рассматриваться отдельно.
В случае а) большую выборочную дисперсию делят наменьшую:
Для проверки используется статистика критерия
Обозначим через nmin объем выборки с меньшей выборочной дисперсией и через nmах – с большей.
По таблице распределения Фишера находим критическую точку с уровнем значимости α/2 и числами степеней свободыnmах-1 и nmin-1.
Если F<Fкр, то основная гипотеза H0принимается, иначе – отвергается
В случае б) делят первую выборочную дисперсию на вторую:
По таблице распределения Фишера находим критическую точку с уровнем значимости α и степенями свободыn-1 и m-1.
Если F<Fкр, то основная гипотеза принимается, иначе отвергается.
27. Проверка статистической гипотезы о статистической взаимосвязи.
Статистической гипотезой называется любое предположение относительно генеральной совокупности. Гипотеза называется параметрической, если в ней содержится некоторое утверждение о параметрах распределения случайной величины(когда сам закон распределения считается известным) и непараметрической в иных случаях.Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. В нем рассматривается зависимость случайного результативного признака У от неслучайного факторного признака Х.
В случае единственного факторного признака Х уравнение взаимосвязи имеет вид:У= фи (х) + Е.Где Е- случайная величина, математическое ожидание которой равно 0, а дисперсия const.В зависимости от фи (х) виды регрессии бывают:
Линейная
Гиперболическая
Показательная
Логарифмическая
Степенная.
28.Критерий согласия. Критерий 
(Пирсона).
Пусть имеется теор.закон распр. р1,р2..рn Значения х1,х2..хnсгрупированны по m интервалам. Есть выборка объёма n: n1,n2..nm; 
Пусть проверяется гип.о выбранном виде закона распр.с.в.1.Расчитывается мера расхождения между наблюденными частотами и теор. Частотами x2по фор-ле:
2.Д/данного уровня значимости α по табл. Х2-распр.нах-ся крит.знач. 
при числе степеней свободы k=m-r-1
3.Если х2> то гип.Н0 отвергается, а если х2≤ то нет основания отказываться от теор.закона распр.