ТЕМА 5.. Методы многомерной оптимизации

Дана некоторая функция многих переменных f(x₁,x₂,x₃,…..,x_n) или 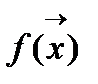надо найти такое значение 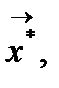при котором функция принимает экстремальное значение (минимальное или максимальное). Процесс поиска экстремального значения иногда называют оптимизацией. называют оптимизируемой или целевой функцией называют вектором параметров оптимизации. В области определения функции может быть несколько экстремумов. Все существующие методы многомерной оптимизации позволяют определить лишь один из экстремумов.

Все методы многомерной оптимизации делятся на два класса: градиентные; безградиентные.

Градиентный метод. Градиентом называется вектор равный сумме произведений частных производных на соответствующие орты. Орта – единичный связанный вектор, направленный вдоль координатной оси.

Основные свойства градиента: Норма градиента определяет скорость изменения функции в направление градиента; Градиент всегда направлен в сторону наиболее быстрого возрастания функции, т.е. в этом направлении норма вектора градиента максимальна; Градиент перпендикулярен линии уровня. Антиградиентом называется вектор, направленный в сторону противоположную градиенту.

Алгоритм метода

1) Дана функция n переменных точность ε, параметр шага h, задаем начальное приближение вычисляем значение функции

2) Вычисляем вектор градиента и единичный вектор градиента

3) Вычисляем новое приближение, делая шаг в направление антиградиента и вычисляем значение функции

4) Проверяем условие Fz < Fx

5) Если условие выполняется, то за начальное приближение принимаем т.е. 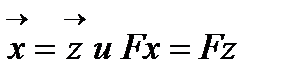, переходим на пункт 2.

6) Иначе, проверяем условие окончания h < ε

7) Если условие выполняется, то выводим Конец алгоритма

8) Если не выполняется, то уменьшаем параметр шага h=h/3 и переходим на пункт 2

Безградиентные методы. Рассматриваются один – симплексный и метод сканирования.

Симплексный метод. Симплексом в n-мерном пространстве называется выпуклый многоугольник с n+1 вершиной. n=2 треугольник n=3 тетраэдр.

Алгоритм

1) Дана функция 2^x переменных точность ε, параметр h, начальное приближение

2) Вычисляем координаты вершин симплекса

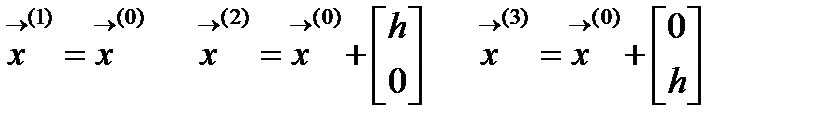
3) Вычисляем значения функции

4) Определяем (рис.2.10.1) худшую вершину и координаты отраженной вершины, она будет лежать на прямой исходящей из худшей вершины и проходящей через середину противоположной грани

I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AGPBmY/GAAAA3QAAAA8AAABkcnMvZG93bnJldi54bWxEj0FLw0AQhe9C/8MyBW92Yyla0m6LFAqC oDQRxduQnWRDs7Mhu7brv3cOgrcZ3pv3vtnusx/UhabYBzZwvyhAETfB9twZeK+Pd2tQMSFbHAKT gR+KsN/NbrZY2nDlE12q1CkJ4ViiAZfSWGodG0ce4yKMxKK1YfKYZJ06bSe8Srgf9LIoHrTHnqXB 4UgHR825+vYGXlt6HD9e2mPOn9TUX6tT9VY7Y27n+WkDKlFO/+a/62cr+OuV4Mo3MoLe/QIAAP// AwBQSwECLQAUAAYACAAAACEABKs5XgABAADmAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRf VHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQAIwxik1AAAAJMBAAALAAAAAAAAAAAAAAAAADEBAABf cmVscy8ucmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAASAAAAAAAAAAAAAAAAAC4CAABk cnMvcGljdHVyZXhtbC54bWxQSwECLQAUAAYACAAAACEAY8GZj8YAAADdAAAADwAAAAAAAAAAAAAA AACfAgAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9wAAAJIDAAAAAA== ">

Рис.6.1. Переход от худшей вершины к отраженной.

5) Сравниваем значения функции

6) Условие выполняется. За новый симплекс принимаем симплекс с вершиной и повторяем с пункта 3

7) Условие не выполняется. Проверяем условие окончания h< ε

8) Условие окончания выполняется. Выводим координаты и значение функции лучшей вершины

9) Условие не выполняется. За принимаем лучшую вершину последнего симплекса, уменьшаем длину грани h=h/3 и повторяем с пункта 2.

Операторы МАТЛАБа позволяют это сделать так:

Пусть функция имеет вид, который задан функцией inline(), начальная точка [0;0]. Используется решатель fminsearch(fxx,[0;0]).

fxx=inline(‘8*x(1)^2+5*x(2)^2+4x(1)*x(2)')

[x,y,opt]=fminsearch(fxx,[0;0])

Метод сканирования. В области исследуемой функции двух переменных выбирается значение одной из переменных, соответствующее краю области поиска. По другой переменной интервал поиска разбивается на равные участки, длина каждого из которых равна шагу поиска. Далее значение функции последовательно определяется во всех точках разбиения и на краях отрезка, наименьшее из них запоминается. Затем увеличивают переменную, значение которой было постоянным, на шаг поиска и повторяют процедуру. И так до тех пор, пока не будет исследована вся область поиска с заранее выбранным шагом по каждой из переменных. Минимальное из всех сохраненных значений минимумов и есть глобальный минимум.

Для повышения точности повторяют сканирование в области, края которой отстоят от найденной точки минимума на величину шага предыдущего сканирования. Новое значение шага сканирования будет многократно меньше