Блок-схема интерполяции многочленом Лагранжа

|
Пример. По заданным точкам: xi=-1 0 1; yi=1 0 1. Определить интерполяционный многочлен L(x).



L(x)=x2
ТЕМА 2. Приближение функции.Аппроксимация. Метод наименьших квадратов (МНК).
Пусть имеются результаты некоторого эксперимента в виде массива значений независимой переменной xi и зависимой переменной yi,. где i=0,1,2,…,n
Требуется отыскать аналитическую зависимость f(x,a0,a1,…,am), являющуюся функцией одной независимой переменной x и параметров a0,a1,a2,…,am, которая наилучшим образом описывала бы эти экспериментальные данные в смысле минимума квадратичного критерия 
Решаем задачу в классе полиномов и функцию f (x,a0,a1,…,am) определим как полином степени m вида:  Надо найти такие значения параметров вектора а, при которых квадратичный критерий рассогласования имел бы минимальное значение.
Надо найти такие значения параметров вектора а, при которых квадратичный критерий рассогласования имел бы минимальное значение. 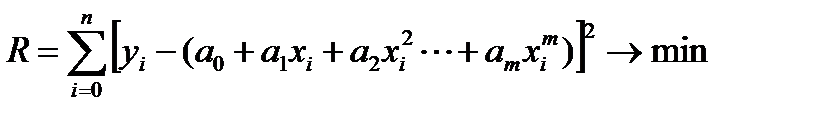 Вывод формулы для определения параметров не представлен. Приводим окончательную формулу вычисления вектора параметров в матричном виде a= inv (Ф’*Ф) *Ф’*y
Вывод формулы для определения параметров не представлен. Приводим окончательную формулу вычисления вектора параметров в матричном виде a= inv (Ф’*Ф) *Ф’*y
Рассмотрим применение расчета для функции (m=2) вида 
Тогда критерий R будет являться функцией трёх переменных a0, a1, a2: 
Для удобства формирования матрицы коэффициентов  и столбца свободных членов
и столбца свободных членов  введем матрицу
введем матрицу  элементы которой определяются через значения независимой переменной xi, i=0,1,2,…,n
элементы которой определяются через значения независимой переменной xi, i=0,1,2,…,n  так как
так как 
В общем случае количество строк в матрице 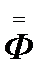 равно количеству точек, а количество столбцов равно количеству параметров, где строка состоит из значений частных производных от функции f(x,a0,a1,…,am) по соответствующему параметру.
равно количеству точек, а количество столбцов равно количеству параметров, где строка состоит из значений частных производных от функции f(x,a0,a1,…,am) по соответствующему параметру.

a= inv(Ф’*Ф) *Ф’*y
Далее представлена блок-схема алгоритма МНК и числовой расчет для полиномиальной функции m=1, n=4 для которой критерий рассогласования оказался равным R=2.3


Блок-схема аппроксимации.
Параллельно(справа) приведен числовой расчет.
| Пример. xi= -1 0 1 2; yi= 2 1 2 4.





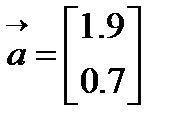


|
ТЕМА 3. Методы численного интегрирования
Пусть на отрезке [a; b] определена непрерывная функция f(x). f=inline(‘<функция>'); Требуется определить значение определенного интеграла  которое численно равно площади S фигуры, ограниченной графиком функции f(x) и осью x, на заданном отрезке [a; b]. Для приближенного вычисления площади, разобьем отрезок [a; b] на n равных элементарных отрезков точками: x0=a, x1= a+h, x2=x1+h,…,xi=xi–1+h,…,xn=b,
которое численно равно площади S фигуры, ограниченной графиком функции f(x) и осью x, на заданном отрезке [a; b]. Для приближенного вычисления площади, разобьем отрезок [a; b] на n равных элементарных отрезков точками: x0=a, x1= a+h, x2=x1+h,…,xi=xi–1+h,…,xn=b,  – шаг разбиения. Значение функции f(x) в точках (рис.3.1) разбиения xi обозначим через yi.
– шаг разбиения. Значение функции f(x) в точках (рис.3.1) разбиения xi обозначим через yi.
|
Рис.3.1. Интегрирование. Разбиение на равные отрезки.
Ниже приведена совокупность команд для построения графика функции
f=inline(‘<функция>');
x=a:h:b;
plot(x,f(x),'k-')
Площадь S можно вычислить как сумму элементарных площадей определенных для соответствующих элементарных отрезков длиной h: S = s0+s1+s2+…si+…..+sn–1 Произвольную площадь si можно вычислить, как определенный интеграл на отрезке [xi;xi+1] от более простой функции φi(x), которой заменим реальную функцию f(x): 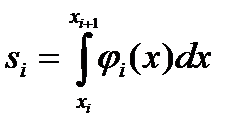 Вид функции φi(x) будет определять название метода.
Вид функции φi(x) будет определять название метода.
Методы прямоугольников. Значение функции φi(x) на отрезке [xi;xi+1] принимается константой
Метод прямоугольников вперед. Для функции φi(x) = yi значения элементарной si и общей S площади можно вычислить как:  , тогда
, тогда 
x=a:h:b-h;
S=h*sum(f(x));
Метод прямоугольников назад. Аналогично, можно вычислить значение S  ,
, 
x=a+h:h:b;
S=h*sum(f(x));
Метод прямоугольников в среднем. Тогда значения элементарной si и общей S площади можно вычислить как 

x=a+h/2:h:b;
S=h*sum(f(x));
Метод трапеций. Функцию φi(x) будем определять как линейную на отрезке [xi;xi+1], т.е. ее график должен проходить через две смежные точки (xi,yi) и (xi+1,yi+1). Функцию φi(x) можно будет представить как интерполяционный многочлен Лагранжа, построенный по двум точкам (xi,yi) и (xi+1,yi+1):  тогда значения элементарной si площади можно вычислить как:
тогда значения элементарной si площади можно вычислить как: 


| x=a:h:b-h; S=h*sum((f(x)+f(x+h))/2); | x=a:h:b; S=trapz(x,f(x)); | x=a:h:b; S=h*trapz(f(x)); |
Метод Симпсона. Определим точку xi+½ = xi+½·h в середине элементарного отрезка [xi;xi+1] и значение функции в этой точке yi+½ Функцию φi(x) будем определять как квадратичную на отрезке [xi;xi+1], т.е. её график должен проходить через три смежные точки (xi,yi),(xi+½ , yi+½) и (xi+1,yi+1). Функцию φi(x) можно будет представить как интерполяционный многочлен Лагранжа, построенный по трём точкам xi, xi+½ и xi+1:

 Тогда значения элементарной si площади можно вычислить как:
Тогда значения элементарной si площади можно вычислить как:


Тогда значения общей S площади можно записать как:


Вычисление в МАТЛАБе
| x=a+h:h:b-h; xs=a+h/2:h:b; S=h/6*(f(a)+f(b)+2*sum(f(x))+4*sum(f(xs))); | S=quad(f,a,b); |
ТЕМА 4. Решение систем нелинейных уравнений
Система нелинейных уравнений (СНУ). В общем случае систему нелинейных уравнений можно записать как:  или
или  Решением СНУ является такой вектор
Решением СНУ является такой вектор 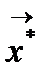 при подстановке которого в систему последняя обращается в тождество.
при подстановке которого в систему последняя обращается в тождество.
Методы простых итераций. При прямом подходе довольно сложно получить итерационную формулу получения эквивалентной системы нелинейных уравнений, позволяющую получить решение СНУ. Поэтому в основном используется метод Ньтона- Рафсона.
Метод Ньютона-Рафсона. Пусть известно некоторое приближение  к решению
к решению  Запишем исходную систему в виде
Запишем исходную систему в виде  где
где 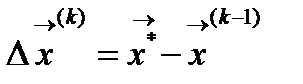 Разложим функцию в ряд Тейлора и ограничимся линейными членами.
Разложим функцию в ряд Тейлора и ограничимся линейными членами. 

Это система линейных уравнений относительно 
Матрица Якоби  Тогда
Тогда 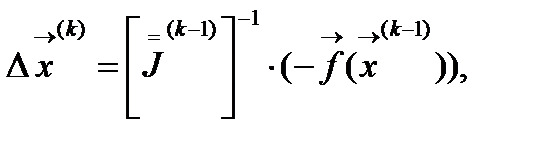 а новое приближение к решению СНУ будет иметь вид:
а новое приближение к решению СНУ будет иметь вид: 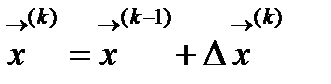 или
или  Условием окончания итерационного процесса является выполнения неравенства
Условием окончания итерационного процесса является выполнения неравенства 
Оператор МАТЛАБа [x,fun]=fsolve(@f,[x1 x2]);
Результат выполнения - значения неизвестных и значение функции.