ТЕМА 6. Методы решения обыкновенных дифференциальных уравнений

Общий вид обыкновенного дифференциального уравнения, устанавливающего связь между независимой переменной x неизвестной функцией y и ее производными y’,y”,…,y⁽ⁿ⁾, может мыть представлен следующим образом:

Решением дифференциального уравнения (интегрированием) является некоторая функциональная зависимость y=y(x), которая при подстановке в уравнение обращает его в тождество.

Общее решение дифференциального уравнения записывается в виде: y=y(x,c₁,c₂,…,c_n), где c₁,c₂,…,c_n произвольные постоянные.

Решение, полученное из общего решения при фиксированных значениях, называется частным решением уравнения. Постоянные c₁,c₂,…,c_n можно определить, задав n условий. Если эти условия заданы как совокупность значений искомой функции и всех ее производных до (n-1) порядка включительно в некоторой точке x₀, то задача решения уравнения называется задачей Коши, а заданные условия: y(x₀)=y₀, y’(x₀)=y’₀, y”(x₀)=y”₀,…, y^n-1(x₀)=y^n-1₀ называются начальными условия.

Если же условия заданы при нескольких значениях x, то задача решения дифференциального уравнения будет называться граничной или краевой задачей.

Рассмотрим дифференциальное уравнение первого порядка: соотношение часто удается записать в виде: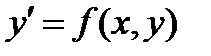

Последнее уравнение называется дифференциальным уравнением, разрешенным относительно производной. Значение производной равно тангенсу угла наклона касательной к графику функции в точке (x,y). Функцию f(x,y) будем называть правой частью дифференциального уравнения.

Общим решением уравнения будет являться семейство функций y=y(x,c₁) различающихся значение постоянной c₁. Задаем одно начальное условие y(x₀)=y₀, которое определяет значение c₁и конкретное частное решение – задача Коши.

Для простейшего дифференциального уравнения y’=3x². Общее решение имеет вид y=x³+c, а подставив в общее решение начальное условие x₀=1, y₀=2 вычислим с=1 и определим частное решение как: y=x³+1

Метод Эйлера. Дано дифференциальное уравнение y’=f(x,y), удовлетворяющее начальному условию y(x₀)=y₀. Требуется найти решение на отрезке [a,b]. Разобьем (рис.2.11.1) отрезок интегрирования на n равных частей: x₀=a, x₁= a+h, x₂=x₁+h,…,x_i=x_i–1+h,…,x_n=b, тогда величина шага интегрирования будет равна:

Рис.7.1. Метод Эйлера.

Значение функции y₁ в точке x₁ можно определить как точку пересечения касательной проведенной к функции y=y(x) в точке (x₀,y₀) с вертикальной прямой проходящей через точку x₁.

Тангенс угла наклона касательной есть значение производной в точке (x₀,y₀) и задается правой частью дифференциального уравнения, т.е. tg(β)=f(x₀,y₀). С другой стороны из геометрического представления метода можно записать: Следовательно Отку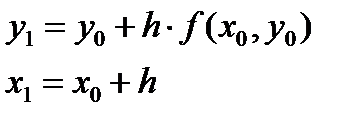да тогда и так далее. Решение будет заключаться в последовательном применении формул: где i = 1, 2, 3, …, n Результат будет представлен функцией заданной таблицей.

Модифицированный метод Эйлера. Графическая интерпретация.

Определяем (рис.2.11.2) точку и вычисляем значение функции в этой точке Значение функции y₁ в точке x₁ определяем, как точку пересечения касательной, вычисленной в точке (x_1/2,y_1/2) и проведенной к функции y=y(x) в точке (x₀,y₀), с вертикальной прямой проходящей через точку x₁.

Рис.7.2. Модифицированный метод Эйлера.

произвольную точку определим

Решение в МАТЛАБе. Используем решатель ode113. Покажем на примере.

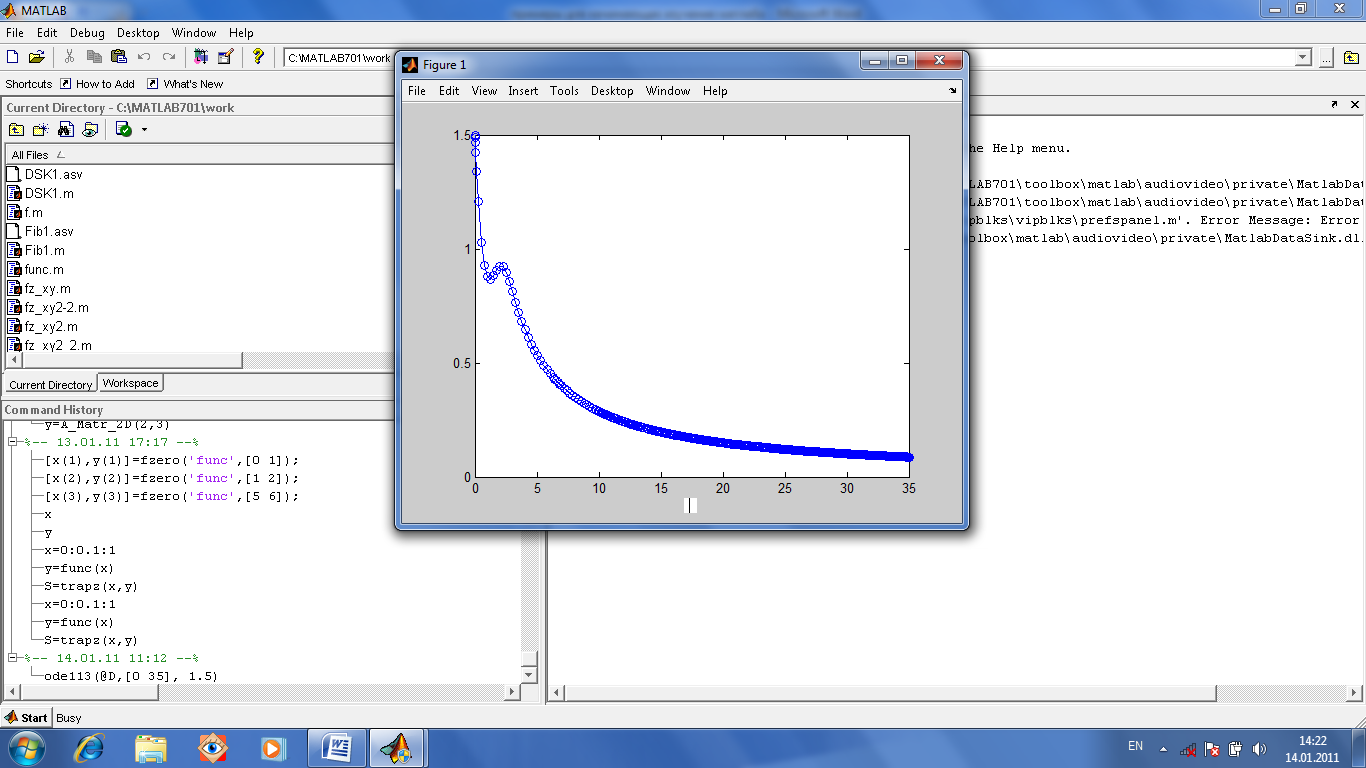
Решим задачу Коши: dx/dt + x =sin xt при x(0)=1.5. Напишем М-функцию. Используем функцию ode113, которая реализует метод Адамса. В качестве ее параметров используются: @D ссылка на М-функцию, [0 35] интервал интегрирования уравнения, начальное условие x(0)=1.5 указано в виде 1,5 на соответствующем месте в списке параметров.

Обращение к функции:

ode113(@D, [0 35], 1.5). Она строит график решения.