1. Понятие дедуктивного умозаключения
Мы уже касались в главе «Логика высказываний» вопроса о том, что такое умозаключение. Повторим вкратце, добавив то, что необходимо для перехода к дедуктивным умозаключениям.
Умозаключение есть рассуждение, в котором на основании одних истинных суждений переходят к другим истинным суждениям.
Напомним символическую запись умозаключения:
A, B, C, D …
F
Здесь A, B, C, D … истинные суждения, на основе которых получают новое знание, они называются посылками. F - новое суждение, называется заключением. Черта означает логическое следование. Все выражение читается так: А, В, С, D..., следовательно, F.
Заключение будет истинным, если выполняются два требования:
1. Посылки должны быть истинными суждениями.
2. Умозаключение должно быть правильно построено.
Проведем важное различие. Все умозаключения можно разделить на два класса. В первый класс войдут умозаключения, для которых выполнение данных двух требований не только необходимо, но и достаточно чтобы получить безусловно истинное, т.е. достоверное, заключение. Достоверность заключения гарантируется чисто формальными правилами. Поэтому нет необходимости обращаться к реальным фактам для проверки истинности заключения.
Во второй класс входят умозаключения, для которых выполнение этих требований является необходимым, но недостаточным условием для получения безусловно истинного, или достоверного, заключения. Само по себе выполнение этих требований обеспечивает лишь вероятностный характер заключения. Существуют, правда, дополнительные приемы, увеличивающие вероятность истинного заключения. Но все же для того, чтобы прийти к безусловно истинному новому знанию, необходимо содержательное исследование самой реальности, это исследование должно включать творческую интуицию, догадку и другие неформальные моменты, лежащие вне собственно логической сферы.
С разделением на дедуктивные и вероятностные умозаключения мы отчасти уже встречались, когда разбирали условно-категорическое умозаключение. Мы подчеркивали, что существуют два его достоверных модуса – утверждающий и отрицающий, обеспечивающие с необходимостью истинность заключения. Это:
| A ® B, A, B | A ® B ,ù B. ù A |
Существуют также два недостоверных модуса, которые обеспечивают истинность заключения лишь с той или иной степенью вероятности:
| A ® B, ù A Возможно, что ù B | , | A®B, B. Возможно, что A |
Умозаключения первого класса, когда достаточно формальных правил для достоверного заключения, называются дедуктивными, от латинского слова deductio – выведение. Это − чисто условные, разделительно-категорические, лемматические умозаключения, достоверные модусы условно-категорического умозаключения, а также непосредственные умозаключения, категорический силлогизм и сориты, которые мы будем разбирать в следующих параграфах.
Умозаключения второго класса называются вероятностными. К ним можно отнести недостоверные модусы условно-категорического умозаключения, а также индуктивное умозаключение(от латинского слова inductio – наведение), аналогию, гипотетическое умозаключение. Умозаключения этого класса имеют свои преимущества. Ближе мы с ними познакомимся в следующей главе.
Почему дедуктивные умозаключения позволяют получать безусловно истинное знание на основании чисто формальных правил?
Дело в том, что такие умозаключения строятся на преобразовании уже готового знания, прежде всего на работе со структурой суждений. При помощи этих преобразований мы извлекаем из суждений новое знание, которое косвенным образом, т.е. потенциально, уже содержится в этих суждениях. Поэтому нет нужды обращаться к реальным фактам. Достаточно работы с суждениями по правилам.
Выражаясь парадоксально, можно сказать так: дедуктивные умозаключения позволяют рассуждать, т.е. думать, «не думая», автоматически, почти не вникая в содержательный смысл самих суждений.
Однако это достоинство дедуктивных умозаключений связано с определенной их ограниченностью. Дедуктивные умозаключения позволяют переходить от знания одной степени общности к знаниям той же либо меньшей степени общности. Но не позволяют переходить к знанию более общего характера.
Например, мы не можем перейти при помощи дедукции от суждения «Все люди смертны» к более общему суждению «Все млекопитающие смертны». Для такого рода обобщений необходимо опираться на другие типы умозаключений, например, такие как индуктивные умозаключения.
2. Непосредственные умозаключения
Дадим определение непосредственного умозаключения:
Умозаключение называется непосредственным, если оно состоит из одной посылки и заключения.
Пример:
Ни один кит не является рыбой.
Ни одна рыба не является китом.
Такого рода умозаключения весьма распространены, мы часто рассуждаем так чисто интуитивно и машинально, не подозревая, что используем ту или иную разновидность непосредственного умозаключения. Основаны они на преобразовании структуры исходного суждения-посылки по определенным правилам.
Можно различать следующие виды непосредственных умозаключений: обращение, превращение, противопоставление предикату, умозаключения по логическому квадрату и на основе единичного суждения.
Обращение. Известно, что суждение есть мысль, в которой нечто сообщается о субъекте. Обращение же – это умозаключение, позволяющее получить определенное знание о предикате.
При обращении субъект и предикат меняются местами, связка остается прежней, квантор перед новым субъектом определяется по правилу:
Если предикат в посылке нераспределен, то он не может быть распределен в качестве субъекта в заключении.
Рассмотрим, как конкретно выглядит умозаключение обращения по всем четырем видам суждений.
1. Общеутвердительное суждение «Все S есть P ». Меняем местами субъект и предикат, связку оставляем прежней, получаем: «Р есть S ».
Теперь необходимо определить квантор при новом субъекте, для этого обращаемся к правилу. Предикат в общеутвердительном суждении нераспределен, так как объем предиката в общеутвердительном суждении лишь частично входит в объем субъекта. Поэтому новый субъект в заключении тоже должен быть нераспределенным. Но это означает, что перед ним должен стоять квантор существования.

| На круговой схеме общеутвердительного суждения наглядно видно, что лишь часть объема предиката Р совпадает с объемом субъекта S. Эта часть на схеме затемнена. Знаки плюс (+) и минус (−) при Р означает, что предикат соответственно распределен или нераспределен. |
Таким образом, имеем следующую символическую запись:
Все S есть Р -..
Некоторые Р -есть S.
Подставив вместо S и Р понятия «щука» и «хищник», получаем содержательное рассуждение:
Все щуки есть хищники.
Некоторые хищники есть щуки.
Подставим вместо S и Р понятия «фиалка» и «цветок», получаем новое содержательное рассуждение:
Все фиалки являются цветами.
Некоторые цветы являются фиалками.
2. Общеотрицательное суждение «Ни одно S не есть Р ». Меняем местами субъект и предикат, связка остается отрицательной, получаем: «Р не есть S ». Определяем квантор перед новым субъектом на основе правила. В отрицательных суждениях предикат распределен.

| Действительно, на круговой схеме видно, что весь объем Р находится вне объема S. Поэтому перед новым субъектом в заключении может стоять квантор общности. |
Символическая запись:
Ни одно S не есть Р +.
Ни одно Р + не есть S.
Используем в качестве посылки афоризм «Счастливые часов не наблюдают». Преобразуем его в общеотрицательное суждение стандартного вида, и получаем несколько неожиданное заключение.
Ни один счастливый не есть тот, кто наблюдает часы.
Ни один из тех, кто наблюдает часы, не является счастливым.
Таким образом, если для кого-то томительно тянется время, то это означает, что в данный момент он не является счастливым человеком. Посмотрим, что получится из выражения «Трус не играет в хоккей».
Ни один трус не есть тот, кто играет в хоккей.
Ни один из тех, кто играет в хоккей, не является трусом.
3. Частноутвердительное суждение «Некоторые S есть Р ». Меняем субъект и предикат местами, связка остается утвердительной: «Р есть S ». Определяем квантор на основе правила.

| Объем предиката частично входит в объем субъекта, т.е. предикат нераспределен, это значит, что новый субъект в заключении тоже не может быть распределен. Поэтому перед ним должен стоять квантор существования. |
Символическая запись:
Некоторые S есть Р -..
Некоторые Р - есть S.
Примеры:
Некоторые космонавты являются любителями рыбной ловли.
Некоторые любители рыбной ловли являются космонавтами.
Некоторые сосны растут в Заполярье.
Часть того, что растет в Заполярье, есть сосны.
4. Частноотрицательное суждение «Некоторые S не есть Р ». При обращении частноотрицательного суждения возникает затруднение. Предикат в отрицательных суждениях распределен, поэтому новый субъект в суждении может быть тоже распределен, таким образом, перед ним можно было бы поставить квантор общности. Получается символическая запись:
Некоторые S не есть Р +..
Ни одно Р + не есть S.
Но круговая схема заключения не совпадет со схемой посылки.
Посылка

|
Заключение

| В посылке объем предиката находится вне части объема субъекта, а в заключении объем предиката находится вне всего объема субъекта. |
Новый субъект в заключении можно сделать нераспределенным, правило обращения не запрещает это сделать, и поставить передсубъектом квантор существования.
Некоторые S не есть Р +..
Некоторые Р -не есть S.
Посылка

| Заключение
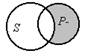
| Снова круговая схема заключения отличается от схемы посылки. |
Заключение, точно соответствующее круговой схеме посылки, должно выглядеть так: «Ни одно Р не есть некоторые S »или «Некоторые Р не есть некоторые S ». Например:
Некоторые животные не являются хищниками.
Некоторые хищники не являются некоторыми животными.
Получилось в качестве заключения неопределенное суждение, не имеющее познавательного смысла. Вывод:
Частноотрицательные суждения – не обращаются.
Но мы можем преобразовать частноотрицательное суждение в частноутвердительное, перенеся частицу «не» из связки в предикат. Например, посылку «Некоторые животные не являются хищниками» переделать в суждение «Некоторые животные являются нехищниками». И тогда выполнить обращение полученного частноутвердительного суждения: «Некоторые нехищники являются животными».
Рассмотрим обращение общеутвердительного и частноутвердительного выделяющих суждений. В этих суждениях предикат всегда распределен. Поэтому обращение как того, так и другого суждения дает в заключении общеутвердительное суждение:
| Все S есть P +., Все P + есть S. | Некоторые S есть P +.. Все P + есть S. |
Содержательные примеры:
Все дочери являются внучками.
Все внучки являются дочерьми.
Некоторые деревья являются яблонями.
Все яблони являются деревьями.
Задание 1. Выполните обращение суждений в следующей последовательности: сначала переведите исходное суждение-посылку в символическую форму, затем обратите его в этой форме и переведите полученное заключение в новое содержательное суждение.
Образец выполнения:
| Инфузории обитают в воде. ® Некоторые из обитающих в воде есть инфузории. | Все S есть Р -.. Некоторые Р - есть S. |
1. Многие дети хорошо играют в шахматы.
2. Радуги прекрасны.
3. Все квадраты являются ромбами с равными сторонами.
4. Ни один ковбой не расстается с многозарядным пистолетом.
5. Значительная часть насекомых не является муравьями.
6. Часть насекомых – муравьи.
Превращение. Это умозаключение позволяет получить новое знание о субъекте через его отношение к дополнению предиката.
При превращении квантор и субъект остаются теми же самыми, но связка меняется на противоположную, а предикат заменяется на дополнение к нему, т.е. Р заменяется на не- Р. Происходит своеобразное двойное отрицание – связки и предиката.
Рассмотрим умозаключение превращения по четырем видам суждений.
1. Общеутвердительное суждение «Все S есть Р ». Заменяем утвердительную связку «есть» на отрицательную «не есть», а предикат Р на его дополнение не- Р. Получаем символическую запись:
Все S есть Р..
Ни одно S не есть не- Р.

| На схеме, совмещающей понятия S, Р, не- Р, видно, что объем субъекта S действительно находится целиком вне объема нового предиката не- Р, который затемнен. |
Содержательные примеры:
Все радуги есть прекрасные явления..
Ни одна радуга не есть непрекрасное явление.
Все люди – несовершенны..
Ни один человек не есть не-несовершенный (т.е. совершенный).
2. Общеотрицательное суждение «Ни одно S не есть Р ». Заменяем отрицательную связку «не есть» на утвердительную «есть», а Р на не- Р. Получаем символическую запись:
Ни одно S не есть Р.
Все S есть не- Р.

| Согласно схеме объем субъекта S целиком входит в объем понятия не- Р. |
Содержательные примеры:
Ни один кит не является рыбой.
Все киты есть нерыбы.
Ни один политический строй не является совершенным.
Любой политический строй – несовершенен.
3. Частноутвердительное суждение «Некоторые S есть Р ». Заменяем связку «есть» на «не есть», а Р на не- Р. Символическая запись:
Некоторые S есть Р..
Некоторые S не есть не- Р.

| Согласно схеме, та часть объема субъекта, которая входит в объем предиката Р (она зачернена), не входит в объем понятия не- Р. |
Содержательные примеры:
Некоторые люди играют в шахматы..
Некоторые люди не есть те, которые не играют в шахматы.
Некоторые животные являются дикими..
Некоторые животные не являются недикими (т.е. домашними).
4. Частноотрицательное суждение «Некоторые S не есть Р ». На этот раз с этим видом суждений не возникает трудностей. Заменяем связку «не есть» на «есть», Р заменяем на не- Р. Символическая запись:
Некоторые S не есть Р.
Некоторые S есть не- Р.

| Согласно схеме, та часть объема субъекта S, которая не входит в объем предиката Р, входит в объем понятия не- Р. |
Содержательные примеры:
Многие животные не являются дикими.
Многие животные являются недикими (домашними).
Некоторые числа не является четными.
Некоторые числа является нечетными.
Выделяющие суждения превращаются снова в выделяющие. В остальном они ведут себя точно так же, как и невыделяющие: общеутвердительные суждения превращаются в общеотрицательные, частноутвердительные превращаются в частноотрицательные и т.д. Например:
Некоторые деревья являются яблонями.
Некоторые деревья не являются не-яблонями.
Возникают трудности с превращением суждений, в которых после субъекта идет глагол с отрицательной частицей «не». Например: «Некоторые деревья не растут в Заполярье».
Здесь необходимо определиться – считать такое суждение утвердительным с опущенной связкой «есть» и предикатом «не растут в Заполярье», или отрицательным – со связкой «не есть» и предикатом «растут в Заполярье». Таким образом, необходимо выбрать один из вариантов:
Некоторые деревья есть то, что не растет в Заполярье.
Некоторые деревья не есть то, что растет в Заполярье.
И определившись, строить превращение, результат которого тоже будет в двух вариантах:
Некоторые деревья не есть то, что растет в Заполярье.
Некоторые деревья есть то, что не растет в Заполярье.
Часто по небрежности определяют исходное суждение-посылку как отрицательную, и затем все-таки включают частицу «не» в предикат, тогда превращение получается неправильным.
Задание 2. Выполните превращение суждений в той же последовательности, в какой до этого выполняли обращение: перевод посылки в символическую форму, далее – превращение ее в символической же форме, и затем перевод получившегося заключения в содержательное суждение. Каждый раз выделяйте предикат.
Образец выполнения:
| Все киты дышат легкими. ® Ни один кит не есть тот, кто не дышит легкими. | Все S есть Р. Ни одно S не есть не- Р |
1. Значительная часть насекомых не является муравьями.
2. Часть насекомых – муравьи.
3. Каждый ковбой не расстается с многозарядным пистолетом.
4. Многие мушкетеры не любили кардинала.
5. Лошади едят овес.
Обратим внимание на следующую особенность превращения. Если мы полученное заключение снова превратим, то вернемся к исходному суждению-посылке. Например:
Некоторые юноши являются футболистами. Þ Некоторые юноши не являются не-футболистами. Þ Некоторые юноши являются не-не-футболистами, т.е. футболистами.
Все люди смертны. Þ Ни один человек не является несмертным, т.е. бессмертным. Þ Все люди являются не-бессмертными, т.е. смертными.
Исследуйте самостоятельно, для всех ли видов суждений двойное превращение означает возвращение к исходному суждению. Исследуйте также, к чему приводит двойное обращение.
Ну а если результат превращения подвергнуть затем обращению? Что получится тогда? Тогда мы получим особый вид непосредственного умозаключения, который называется противопоставлением предикату.
Противопоставление предикату. Это умозаключение позволяет получать знание о дополнении предиката, т.е. знание о не- Р.
Противопоставление предикату выполняется в два шага: сначала исходное суждение-посылка подвергается превращению, а затем полученное заключение обращается. В окончательном заключении субъектом выступает дополнение предиката, т.е. не- Р, предикатом становится субъект посылки, т.е. S, связка меняется на противоположную, квантор меняется в общеотрицательном суждении и остается прежним в остальных случаях. Рассмотрим это умозаключение по разным видам суждений.
1. Общеутвердительное суждение «Все S есть Р ». Заменяем S на не- Р, «есть» на «не есть», Р на S, квантор прежний. Получаем символическую запись:
Все S есть Р.
Ни одно не- Р не есть S
Построим заключение по шагам: Все S есть Р Þ превр. Þ Все S не есть не- Р + Þ обращ. Þ Ни одно не- Р + не есть S.

| На схеме видно, что объем нового субъекта не- Р целиком находится вне объема прежнего субъекта S. |
Приведем примеры, причем для ясности будем выделять курсивом предикат посылки.
Все радуги - прекрасны..
Ни одно не прекрасное явление не есть радуга.
Все люди – несовершенны..
Ни одно совершенное (существо) не являются человеком.
2. Общеотрицательное суждение «Ни одно S не есть P ». Заменяем S на не- P, «не есть» на «есть», P на S, меняем квантор.
Ни одно S не есть P.
Некоторые не- P есть S
Строим заключение по шагам: Ни одно S не есть P Þ превр. Þ Все S есть не- P - Þ обращ. Þ Некоторые не- P - есть S.

| Согласно схеме, лишь часть объема нового субъекта не- P совпадает с объемом прежнего субъекта S. |
Содержательные примеры:
Ни один кит не является рыбой.
Некоторые из не рыб есть киты.
Ни одно число, оканчивающееся на 7, не есть четное.
Некоторые не четные числа оканчиваются на 7.
3. Частноутвердительное суждение «Некоторые S есть P ». Этот вид суждений при превращении переходит в частноотрицательное суждение, которое, как известно, не обращается. Соответственно, противопоставление предикату на частноутвердительных суждениях не выполняется.
4. Частноотрицательное суждение «Некоторые S не есть P ». Заменяем S на не- P, «не есть» на «есть», P на S, квантор остается тот же самый.
Некоторые S не есть Р.
Некоторые не- Р есть S
Получение заключения по шагам: Некоторые S не есть P Þ превр. Þ Некоторые S есть не- P - Þ обращ. Þ Некоторые не- P -есть S.

| На схеме видно, что часть объема нового субъекта не- P совпадает с той частью объема прежнего субъекта S (она зачернена),которая не входит в объем предиката P. |
Содержательные примеры:
Многие домашние животные не являются млекопитающими.
Некоторые не млекопитающие являются домашними животными.
Некоторые птицы не летают.
Некоторые из тех, кто не летает, есть птицы.
Задание 3. Выполните противопоставление предикату суждений в той же последовательности, в какой до этого делали обращение и превращение. Образец выполнения:
| Волга впадает в Каспийское море. ® Ни одна из рек, не впадающих в Каспийское море, не есть Волга. | Все S есть Р. Ни одно не- Р не есть S |
1. Часть насекомых – муравьи.
2. Многие мушкетеры не любили кардинала.
3. Лошади едят овес.
4. Трус не играет в хоккей.
Мы рассмотрели обращение, превращение и противопоставление предикату. Третий вид непосредственного умозаключения интересен тем, что он строится как комбинация первых двух видов: превращение + обращение.
Ну а если мы результат противопоставления предикату снова превратим? Тогда мы получим вид непосредственного умозаключения, который не приводится обычно в литературе по логике, но который вполне реален. Итак: превращение + обращение + превращение. Что же получится? Рассмотрим на примере общеутвердительного суждения.
Все S есть P Þпревр.ÞНи одно S не есть не-P Þобращ.®Ни одно не-P не есть S Þпревр. ÞВсе не-P есть не-S.
Получилось общеутвердительное суждение об отношении дополнения предиката к дополнению субъекта. Содержательный пример:
Все радуги прекрасны..
Все непрекрасное есть нерадуга.
Таким образом, мы вывели новое знание, которое косвенно уже содержалось в исходном суждении-посылке.
Сделаем из любопытства еще один шаг, снова обратим то, что получилось, таким образом, имеем: «Некоторое не- S есть не- P ».
Получили частноутвердительное суждение об отношении дополнения субъекта к дополнению предиката. Посмотрим на примере суждения про радугу: «Некоторые нерадуги – непрекрасны».
Сделаем еще один шаг, применим превращение и к этому результату, получаем: «Некоторые нерадуги не есть прекрасны».
Получилось частноотрицательное суждение, которое уже не обращается. Поэтому здесь остановимся. Однако можно поэкспериментировать с другими видами суждений: общеотрицательными, частноутвердительными и частноотрицательными. Можно сначала обратить исходное суждение, а затем превратить результат, посмотреть, что получится, и сделать дальнейшее обращение.
Таким образом, мы входим в область особых видов непосредственного умозаключения, которым по всей вероятности нет пока названий. Важно подчеркнуть, что логика, даже так называемая традиционная, отнюдь не закрыта для исследований и экспериментов.
Попробуйте самостоятельно открыть новые виды непосредственных умозаключений через различные комбинации обращения и превращения.
Умозаключения по логическому квадрату. Этот тип умозаключений строится на учете отношений между суждениями: подчинения, частичной совместимости, противоположности и противоречия.
Напомним, между какими суждениями существуют эти отношения и каким образом они выражаются.
Подчинение характеризует отношение между общеутвердительным (А) и частноутвердительным (I), а также общеотрицательным (Е) и частноотрицательным (О) суждениями. Это отношение выражается формулами А ® I и E ® О, где символ ® означает импликацию.
Частичная совместимость характеризует отношение между частноутвердительным (I) и частноотрицательным (О) суждениями. Выражается формулой I Ú O, где символ Ú означает слабую дизъюнкцию.
Отношение противоположности характерно для общеутвердительного (А) и общеотрицательного (Е) суждений, оно выражается формулами ù(A · Е) или ù A Úù Е.
Наконец, отношение противоречия существует между общеутвердительным (А) и частноотрицательным (О), а также между общеотрицательным (Е) и частноутвердительным (I) суждениями. Выражается формулами A Ñ O и E Ñ I, где символ Ñ означает сильную дизъюнкцию.
Рассмотрим, какие непосредственные умозаключения соответствуют различным видам суждений на основе этих отношений.
1. Общеутвердительное суждение, А. Перепишем формулы тех отношений, в которых присутствует суждение А, и поставим рядом с формулами само суждение А: А ® I, А; ù A Úù E, A; A Ñ O, А.
Мы получили запись посылок умозаключений логики высказываний – утверждающего модуса условно-категорического умозаключения, отрицающе-утверждающего (посылку А можно рассматривать как отрицание суждения ù А) и утверждающе-отрицающего модусов разделительно-категорического умозаключения. Выведем из этих посылок соответствующие заключения.
| Подчинение А ® I, А, I | Противоположность ù A Úù E, A, ù B | Противоречие A Ñ O, А. ù O |
Перепишем умозаключения, оставив в качестве посылки лишь суждение А. Получаем так называемые непосредственные умозаключения по логическому квадрату при общеутвердительном суждении. Дадим их в виде одной формулы, поставив под чертой все три заключения:
| А. I, ù E, ù O |
Если говорить точно, это не совсем непосредственные умозаключения, т.к. посылок в действительности каждый раз не одна, а две – сложное высказывание и простое суждение. Но в литературе такие умозаключения принято относить к непосредственным.
Перепишем полученные умозаключения в обычном виде, причем все три заключения также дадим одно под другим, не переписывая каждый раз посылку.
Все S есть P.
Некоторые S есть P (подчинение).
Неверно, что ни одно S не есть P (противоположность).
Неверно, что некоторые S не есть P (противоречие).
Содержательный пример:
Все деревья - живые существа.
Некоторые деревья – живые существа [1].
Неверно, что ни одно дерево не есть живое существо.
Неверно, что некоторые деревья не есть живые существа.
Мы рассмотрели вариант с общеутвердительным суждением в качестве посылки, причем подразумевалось, что это суждение является истинным. Поставим вопрос о том, какие умозаключения возможны при условии, что общеутвердительное суждение ложно, следовательно, при истинном суждении «Неверно, что А » в качестве посылки?[2].
| Подчинение А ® I ,ù А, ? | Противоположность ù A Úù E ,ù A, ? | Противоречие A Ñ O ,ù А. ù O |
Лишь в третьем случае – на основе отношения противоречия – получается достоверное заключение. Этот случай перепишем в виде непосредственного умозаключения:
| ù А, ù O | Неверно, что все S есть P. Некоторые S не есть P. |
Пример:
Неверно, что все люди играют в шахматы.
Некоторые люди не играют в шахматы.
2. Общеотрицательное суждение, Е. Перепишем формулы, где присутствует суждение Е и поставим рядом это суждение: E ® О, Е; ù A Úù Е, Е; E Ñ I, E.
Снова получили посылки умозаключений логики высказываний. Выводим заключения:
| Подчинение E ® О, Е, О | Противоположность ù A Úù Е, Е, ù A | Противоречие E Ñ I, E. ù I |
В сокращенном виде:
| Е. О, ù A, ù I |
Получили непосредственные умозаключения по логическому квадрату при общеотрицательном суждении в качестве посылки.
Ни одно S не есть P.
Некоторые S не есть P (подчинение).
Неверно, что все S есть P (противоположность).
Неверно, что некоторые S есть P (противоречие).
Содержательный пример:
Ни один кит не дышит жабрами.
Некоторые киты не дышат жабрами.
Неверно, что все киты дышат жабрами.
Неверно, что некоторые киты дышат жабрами.
Рассмотрим вариант с ложным общеотрицательным суждением, т.е. когда в качестве посылки выступает суждение «Неверно, что Е ».
| Подчинение E ® О,ù Е, ? | Противоположность ù A Úù Е,ù Е, ? | Противоречие E Ñ I ,ù E. I |
Снова лишь в третьем случае – отношение противоречия – получаем достоверное заключение, перепишем этот случай в виде непосредственного умозаключения.
| ù E, I | Неверно, что ни одно S не есть Р. Некоторые S есть Р. |
Пример:
Неверно, что ни один человек не играет в шахматы.
Некоторые люди играют в шахматы.
3. Частноутвердительное суждение, I. Переписываем формулы, содержащие суждение I, и ставим рядом само это суждение: А ® I, I; I Ú O, I; E Ñ I, I.
Из этих посылок согласно умозаключениям логики высказываний выводим заключения.
| Подчинение А ® I, I, ? | Частичная совместимость I Ú O, I, ? | Противоречие E Ñ I, I. ù E |
Лишь в третьем случае, т.е. на основе отношения противоречия, получается достоверное заключение, перепишем его в виде непосредственного умозаключения:
| I, ù E | Некоторые S есть Р. Неверно, что ни одно S не есть Р. |
Пример:
Некоторые люди играют в шахматы.
Неверно, что ни один человек не играет в шахматы.
Перейдем к варианту с ложным частноутвердительным суждением, т.е. с суждением «Неверно, что I » в качестве посылки.
| Подчинение А ® I, ù I, ù А | Частичная совместимость I Ú O, ù I, О | Противоречие E Ñ I, ù I. E |
Перепишем умозаключения в сокращенном виде.
| ù I. ù А, О, E |
Получили непосредственные умозаключения по логическому квадрату при ложном частноутвердительном суждении в качестве посылки. Напишем соответствующие логические выводы:
Неверно, что некоторые S есть P.
Неверно, что все S есть P (подчинение).
Некоторые S не есть P (частичная совместимость).
Ни одно S не есть P (противоречие).
Пример:
Неверно, что некоторые пингвины живут в Африке.
Неверно, что все пингвины живут в Африке.
Некоторые пингвины не живут в Африке.
Ни один из пингвинов не живет в Африке.
4. Частноотрицательное суждение, О. Переписываем формулы с суждением О и ставим рядом само это суждение. Получаем посылки логики высказываний: E ® O, O; I Ú O, O; A Ñ O, O. Выводим возможные заключения:
| Подчинение E ® O, O, ? | Частичная совместимость I Ú O, O, ? | Противоречие A Ñ O, O. ù А |
Достоверное заключение получается лишь в случае отношения противоречия, перепишем его в виде непосредственного умозаключения:
| O, ù А | Некоторые S не есть P. Неверно, что все S есть P. |
Пример:
Некоторые люди не играют в шахматы.
Неверно, что все люди играют в шахматы.
Перейдем к варианту, когда в качестве посылки выступает суждение «Неверно, что О ». Переписываем формулы с суждением О и ставим рядом это суждение: E ® O, ù O; I Ú O, ù O; A Ñ O, ù O. Получаем следующие умозаключения логики высказываний:
| Подчинение E ® O, ù O, ù E | Частичная совместимость I Ú O, ù O, I | Противоречие A Ñ O, ù O. A |
Переписываем умозаключения в виде непосредственных умозаключений:
| ù O. ù E, I, A |
Неверно, что некоторые S не есть P
Неверно, что ни одно S не есть P (подчинение).
Некоторые S есть P (частичная совместимость).
Все S есть P (противоречие).
Пример:
<