Если функция регрессии линейна, то говорят о линейной регрессии. Модель линейной регрессии (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.
Например, Кейнсом была предложена формула такого типа для моделирования зависимости частного потребления С от располагаемого дохода I: 
, где 
- величина автономного потребления, b 
- предельная склонность к потреблению. Однако при использовании этой модели при анализе конкретных данных мы практически всегда будем иметь определенную погрешность, так как строгой функциональной зависимости между этими показателями нет. Однако никто не будет отрицать, что люди (домохозяйства) с большим доходом имеют большее в среднем потребление.
Данная ситуация наглядно представлена на рис. 2.
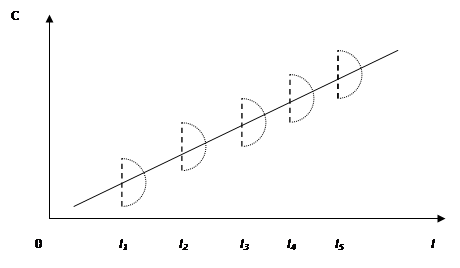
Рис. 2.
Из предыдущих рассуждений ясно, что линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием 
зависимой переменной Y и одной объясняющей переменной X (
- значения независимой переменной в 
-м наблюдении, 
).
(5)
Отметим, что принципиальной в данном случае является линейность по параметрам 
и 
уравнения.
Для отражения того факта, что каждое индивидуальное значение 
отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (5) случайное слагаемое 
(6)
Соотношение (6) называется теоретической линейной регрессионной моделью; и - теоретическими параметрами (теоретическими коэффициентами) регрессии; - случайным отклонением.
Следовательно, индивидуальные значения 
представляются в виде суммы двух компонент - систематической 
и случайной (), причина появления которой достаточно подробно рассмотрена ранее. В общем виде теоретическую линейную регрессионную модель будем представлять в виде
. (7)
Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно.
Таким образом, задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным 
, , для переменных X и Y:
а) получить наилучшие оценки неизвестных параметров а и b;
б) проверить статистические гипотезы о параметрах модели;
в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).
Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии
, (8)
где - оценка условного математического ожидания 
; 
и 
- оценки неизвестных параметров а и b, называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном случае
(9)
где отклонение 
- оценка теоретического случайного отклонения .
В силу несовпадения статистической базы для генеральной совокупности и выборки - оценки и практически всегда отличаются от истинных значений коэффициентов а и b что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок.
Задача состоит в том, чтобы по конкретной выборке , , найти оценки и неизвестных параметров а и b так, чтобы построенная линия регрессии являлась бы наилучшей в определенном смысле среди всех других прямых. Другими словами, построенная прямая должна быть «ближайшей» к точкам наблюдений по их совокупности. Мерами качества найденных оценок могут служить определенные композиции отклонений , . Например, коэффициенты и эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации следующей суммы:
.
Этот метод нахождения коэффициентов является самым распространенным и теоретически обоснованным. Он получил название метод наименьших квадратов (МНК). Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств.
Среди других методов определения оценок коэффициентов регрессии отметим метод моментов (ММ) и метод максимального правдоподобия (ММП).
4. Метод наименьших квадратов
Пусть по выборке , , требуется определить оценки и эмпирического уравнения регрессии (8). В этом случае при использовании МНК минимизируется следующая функция (рис. 3):
. (10)
Рис. 3.
Нетрудно заметить, что функция Q является квадратичной функцией двух параметров и (
), поскольку , - известные данные наблюдений. Так как функция Q непрерывна, выпукла и ограничена снизу 
, то она имеет минимум.
Необходимым условием существования минимума функции двух переменных (10) является равенство нулю ее частных производных по неизвестным параметрам и [1]:
(11)
(12)
Так как 
, 
, 
, 
для заданной выборки являются по сути числами, то имеем систему 2-х линейных алгебраических уравнений с двумя неизвестными и , решить которую можно любым из известных методов (подстановкой, Гаусса, Крамера, обратной матрицы).
Удобно получить и пользоваться готовыми формулами для вычисления коэффициентов регрессии. Введем средние арифметические
, 
, 
, 
.
Разделив оба уравнения системы (12) на п, получим:
(13)
Таким образом, по МНК оценки параметров и определяются по формулам (13).
Нетрудно заметить, что можно вычислить по формуле:
. (14)
Тогда
(15)
где rxy - выборочный коэффициент корреляции; Sx, Sy - стандартные отклонения. Таким образом, коэффициент регрессии пропорционален ковариации и коэффициенту корреляции, а коэффициенты пропорциональности служат для соизмерения перечисленных разномерных величин.
Итак, если коэффициент корреляции r ху уже рассчитан, то легко может быть найден коэффициент парной регрессии по формуле (15).
Если, кроме уравнения регрессии Y на X (
), для тех же эмпирических данных найдено уравнение регрессии X на Y (
), то произведение коэффициентов и 
равно 
:
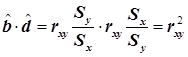. (16)
Отметим, что коэффициенты 
и находятся по формулам, аналогичным формулам (13):
(17)
Характеристики оценок, получаемых по данному методу, следуют из теоремы Гаусса-Маркова.
Теорема Гаусса-Маркова. В предположениях для парной линейной регрессионной модели с пространственной выборкой оценки коэффициентов регрессии а и b, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Общий смысл: оценки коэффициентов линейной регрессии а и b, полученные методом наименьших квадратов, являются в определенном смысле «наилучшими» из всех оценок.
Выводы
Проведенные рассуждения и формулы 10 - 17 позволяют сделать ряд выводов:
1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитывать.
2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.
3. Согласно второй формуле соотношения (13), эмпирическая прямая регрессии обязательно проходит через точку 
.
4. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений 
, а также среднее значение отклонения 
равны нулю.
Действительно, из формулы 
в соотношении (11) следует, что 
.
5. Случайные отклонения не коррелированы с наблюдаемыми значениями 
зависимой переменной Y.
Для обоснования данного утверждения покажем, что ковариация между Y и е равна нулю. Действительно,
.
Покажем, что 
.Просуммировав по все соотношения (9), получим: 
, так как .
Разделив последнее соотношение на п, имеем: 
.
Вычитая из (9) полученное соотношение, приходим к следующей формуле:
. (18)
Тогда
.
Следовательно, 
.
6. Случайные отклонения не коррелированы с наблюдаемыми значениями независимой переменной X.
Действительно, 
в силу второй формулы системы (11) (доказательство выносится для самостоятельной работы). Случайные отклонения , не коррелированы с наблюдаемыми значениями зависимой переменной Y.
Вопросы для самоподготовки
1. Что такое функция регрессии?
2. Чем регрессионная модель отличается от функции регрессии?
3. Назовите основные причины наличия в регрессионной модели случайного отклонения.
4. Назовите основные этапы регрессионного анализа.
5. Что понимается под спецификацией модели, и как она осуществляется?
6. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?
7. Дайте определение теоретической линейной регрессионной модели.
8. В чем суть метода наименьших квадратов (МНК)?
9. Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.
10. Как связаны эмпирические коэффициенты линейной регрессии с выборочным коэффициентом корреляции между переменными уравнения регрессии?
11. Какие выводы можно сделать об оценках коэффициентов регрессии и случайного отклонения, полученных по МНК?
12. Проинтерпретируйте коэффициенты эмпирического парного линейного уравнения регрессии.
13. Какое из следующих утверждений истинно, ложно, не определено? Почему?
а) Случайная погрешность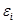 
и отклонение 
совпадают.
б) В регрессионной модели объясняющая переменная является фактором изменения зависимой переменной.
в) Линейное уравнение регрессии является линейной функцией относительно входящих в него переменных.
г) Коэффициенты теоретического и эмпирического уравнений регрессии являются по сути СВ.
д) Значения объясняющей переменной парного линейного уравнения регрессии являются СВ.
е) Коэффициент 
эмпирического парного линейного уравнения регрессии показывает процентное изменение зависимой переменной Y при однопроцентном изменении X.
ж) Коэффициент регрессии Y на X имеет тот же знак, что и коэффициент корреляции 
.
з) МНК удобен тем, что нахождение оценок коэффициентов регрессии сводится к решению системы линейных алгебраических уравнений.
и) Парная линейная регрессионная модель имеет слабую практическую значимость, так как любая экономическая переменная зависит не от одного, а от большого числа факторов.
14. Можно ли ожидать, с вашей точки зрения, наличия зависимости между следующими показателями:
а) ВНП и объем чистого экспорта;
б) объем инвестиций и процентная ставка;
в) расходы на оборону и расходы на образование;
г) оценки в школе и оценки в университете;
д) объем импорта и доход на душу населения в некоторой стране;
е) цена на кофе и цена на чай?
В случае положительного ответа оцените направление зависимости (прямая или обратная), а также решите, какая из переменных будет в этих случаях объясняющей, а какая - зависимой.
15. Как вы считаете, если по одной и той же выборке рассчитаны регрессии Y на X и X на Y, то совпадут ли в этом случае линии регрессии?
16. Суть МНК состоит в:
а) минимизации суммы квадратов коэффициентов регрессии;
б) минимизации суммы квадратов значений зависимой переменной;
в) минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии;
г) минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии.
Выберите правильные ответы.
17. Если переменная X принимает среднее по выборке значение 
, то:
а) наблюдаемая величина зависимой переменной Y равна среднему значению 
;
б) рассчитанное по уравнению регрессии 
значение переменной Y в среднем равно , но не обязательно равно ему в каждом конкретном случае;
в) рассчитанное по уравнению регрессии значение переменной Y равно среднему значению ;
г) отклонение значения 
минимально среди всех других отклонений.
Какой из выводов вам представляется верным и почему?
[1] В последующих формулах для упрощения знаки сумм будем писать без индексов, предполагая, что суммирование ведется от до. Также для переменных с индексом будем подразумевать, что (если не указано иное).