Лекция 2
Тема:Теория числовых последовательностей
План
1. Числовая последовательность;
2. Предел числовой последовательности;
3. Монотонные последовательности
4.Частичные последовательности и частичные пределы;
5.Нижний и верхний пределы;
6. Теорема Больцано-Вейерштрасса.
Определение 1. Пусть каждому натуральному числу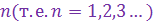 
по некоторому закону поставлено в соответствие действительное число 
. Тогда говорят, что задана числовая последовательность 
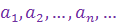, обозначаемая (). Числа 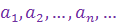, называются членами последовательности: 
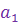- первым членом последовательности, 
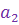- вторым, - 
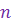-м или общим членом последовательности. Последовательность может быть задана с помощью формулы 
, выражающей 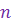– й член последовательности через его номер 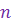. Такую формулу называют формулой общего члена последовательности.
Примеры.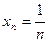 
, 
.
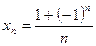Определение 2. Число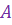 
называется пределом последовательности (), если для любого положительного числа 
можно подобрать такой номер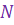 
члена последовательности, зависящей от , что для всех членов последовательности с номерами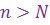 
будет выполнено неравенство 
.
Если 
) имеет своим пределом число 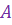, то говорят, что ) сходится (или стремится) к 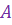и обозначают это так:
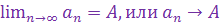. Если последовательность () не имеет предела, то говорят, что она расходится. Используя свойства модуля, неравенство можно записать так: 
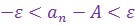или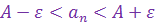 
.
Интервал (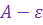
; 
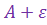) называется – окрестностью числа .
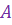Если изобразить числа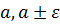 
и значения 
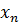последовательности точками на числовой оси, то получится наглядное геометрическое истолкование предела последовательности. Какой бы малый отрезок (длины 2 
) с центром в точке 
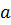ни взять, все точки 
, начиная с некоторой из них, должны попасть внутрь этого отрезка (так что вне его может остаться разве лишь конечное число этих точек).
|
|
В случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.
Определение 3. Последовательность называется бесконечно малой, если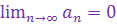 
, т.е. для любого 
найдется номер 
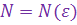такой, что при всех 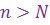будет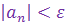 
. Иначе, в любом интервале (
; 
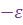) находится бесконечно много членов этой последовательности, а вне ее находится лишь конечное число членов.
Для того чтобы последовательность 
имела своим пределом постоянное число 
, необходимо и достаточно, чтобы разность меду ними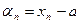 
была бесконечно малой.
Примеры бесконечно малых. 1) 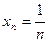. 2)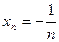 
.
Определение 4. Последовательность называется возрастающей, если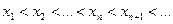 
,
т.е. если из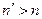 
следует 
.
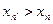Определение 5. Последовательность называется неубывающей, если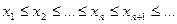 
,
т.е. если из 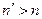следует 
.
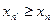Определение 6. Последовательность называется убывающей, если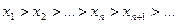 
,
т.е. если из 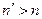следует 
.
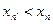Определение 7. Последовательность называется невозрастающей, если 
,
т.е. если из 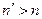следует .
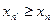Число e. Последовательность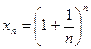 
является возрастающей и ограниченной. Следовательно, она сходится. Её предел обозначают буквой e, т.е.
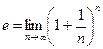. (1)
Доказательство. Отметим, что при k ³1 справедливо неравенство k! = k (k -1)…2×1³ 2k-1. По формуле бинома Ньютона получаем
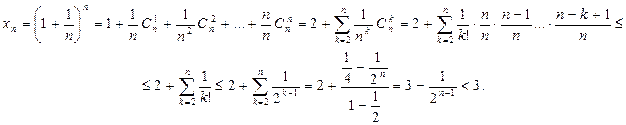
Замечание. Предел последовательности (1) называют числом e или неперовым числом.
Частичные последовательности и частичные пределы.
Определение 1 Последовательность 
, которая составлена из членов последовательности и в которой порядок следования её элементов совпадает с их порядком следования в исходной последовательности , называется подпоследовательностью этой последовательности.
|
|
Определение 2. Если частичная последовательность сходится, то её предел называется частичным пределом исходной последовательности
Теорема 1. Если последовательность имеет определённый предел a, то тот же предел имеет и частичная последовательность .
Определение 3. Число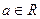 
называется предельной точкой числовой последовательности , если любая её окрестность содержит бесконечное число членов последовательности.
Частичный предел последовательности является одновременно и её предельной точкой.
Определение 4. Наибольший (наименьший) частичный предел числовой последовательности называется её верхним (нижним) пределом и обозначается символом
.
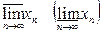Теорема 2. Любая числовая последовательность имеет верхний и нижний пределы.