Теорема Больцано-Вейерштрасса. Критерий Коши.

Определение 1. Пусть { x_n } некоторая последовательность и пусть { k_n }некоторая строго возрастающая последовательность натуральных чисел. Тогда последовательность 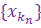называют подпоследовательностью данной последовательности.

Теорема 1 (Болцано-Вейерштрасса). Из всякой ограниченной последовательности { x_n } можно выбрать сходящуюся подпоследовательность.

Доказательство. Так как последовательность { x_n } ограничена, то найдется такое число с, что | x_n | £ с для всех n Î N. Разделим отрезок I₀ = [- с, c ] пополам. Тогда в одной из половин, назовем ее I₁, содержится бесконечно много членов последовательности { x_n }. Обозначим его через I₁ и в качестве первого члена искомой подпоследовательности возьмем какой-нибудь элемент 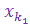Î I₁. Положим y ₁ = .

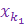Разделим отрезок I₀ = [- с, c ] пополам. Тогда в одной из половин, назовем ее I₁, содержится бесконечно много членов последовательности { x_n }. В качестве первого члена искомой подпоследовательности возьмем какой-нибудь элемент 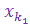Î I₁. Положим y ₁ = .

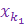Разделим отрезок I₁ пополам. Тогда в одной из половин назовем ее I₂ содержится бесконечно много членов последовательности { x_n }. В качестве второго члена искомой подпоследовательности возьмем какой-нибудь элемент 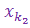Î I₂, c n ₂> n ₁. Положим y ₂ = 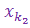. Повторяя эту процедуру с отрезком I₂, найдем отрезок I₃ и член 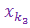. Продолжая этот процесс получим такие подпоследовательность { y_m }= 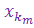последовательности { x_n } и последовательность вложенных отрезков { I_m }, что y_m = 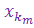, y_m Î I_m, n_m < n_{m +1}, при всех m Î N.

Докажем, что { y_m }сходится. В силу того, что длина d _m = c /2 ^{m -1}, то d _m ®0 при m ®¥. Следовательно по лемме Кантора последовательность { I_m } вложенных отрезков стягивается и все отрезки имеют единственную общую точку a. Существует 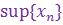.Пусть I_m = [ a_m, b_m ]. Тогда .

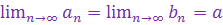Определение 2. Последовательность { x_n } некоторая фундаментальной последовательностью или последовательностью Коши, если для любого положительного числа eнайдется такое число n ₀ Î N, что для всех n, m > n ₀ выполняется неравенство

| x_n - x_m | < e (1)

Теорема 1 (Критерий Коши). Последовательность { x_n } сходится тогда и только тогда, когда она фундаментальная.

Доказательство. Необходимость. Пусть последовательность { x_n } сходится к числу а. Пусть e - любое положительное число. По определению сходимости найдется такое число n ₀ Î N, что для всех n, m > n ₀ выполняются неравенства | x_n - a | < e / 2, | x_m - a | < e / 2. Отсюда при всех n, m > n ₀ выполняется неравенство

| x_n - x_m | = |(x_n - a) - (x_m - a)| £ | x_n - a | + | x_m - a | £ e / 2 + e / 2 = e.

Отсюда по определению последовательность { x_n } - фундаментальная.

Достаточность. Пусть последовательность { x_n } - фундаментальная. Докажем, что она ограничена. Возьмем e=1. По определению найдется такое число k Î N, что для всех n, m > k выполняется неравенство | x_n - x_m | < 1. Тогда

| x_n | £ | x_n - x_k | + | x_k | £ 1+ | x_k | = c ₁.

Таким образом, для всех n Î N имеем

| x_n | £ max(| x ₁|, | x ₂|, …, | x_k |, c ₁)= c.

По теореме Болцано-Вейерштрасса существует сходящаяся подпоследовательность { y_m }= 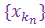® a. Возьмем любого положительного числа e. По определению сходимости для числа e / 2найдется такое число n ₁ Î N, что для всех m > m ₁ выполняется неравенство | y_n - a | < e / 2. По определению фундаментальной последовательности найдется такое число n ₂ Î N, что для всех n, m > n ₂ выполняется неравенство | x_n - x_m | < e / 2. Полагаем n ₀ = max(n ₁, n ₂). Тогда для всех n > n ₀

| x_n - a | £ | x_n - y_k + y_k - a | £ | x_n - y_k | + | y_k - a | < e / 2+e / 2=e.

Следовательно, последовательность { x_n } сходится.