Показатели Ляпунова некоторой линейной стационарной системы
Курсовая работа
Исполнитель:
Студентка группы М-32
Лукьянович А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
Зверева Т.Е.
Гомель 2005
Содержание
Введение
1. Характеристические показатели Ляпунова
2. Теорема Ляпунова. Спектр системы
Заключение
Список использованной литературы
Введение
В данной курсовой работе рассматривается линейная стационарная система.
Линейной стационарной системой называется система вида
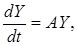
где  − постоянная матрица,
− постоянная матрица, 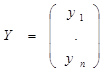 .
.
Общее решение линейной стационарной системы имеет вид
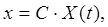
где 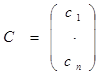 - постоянный вектор,
- постоянный вектор,
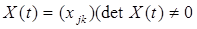 ) - фундаментальная матрица (иными словами, фундаментальная система решений, записанная в виде матрицы), то есть матрица, состоящая из n линейно независимых ее решений
) - фундаментальная матрица (иными словами, фундаментальная система решений, записанная в виде матрицы), то есть матрица, состоящая из n линейно независимых ее решений
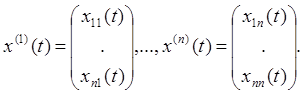
Цель курсовой работы - найти спектр этой системы.
Множество всех собственных характеристических показателей решений дифференциальной системы называется ее спектром.
Таким образом, главная задача курсовой работы - найти различные характеристические показатели Ляпунова заданной линейной стационарной системы.
Характеристические показатели Ляпунова
Рассмотрим следующую линейную стационарную систему
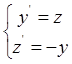
(1).
Найдем общее решение этой системы. Для этого решим ее методом исключения.
Продифференцировав первое уравнение системы (1) и пользуясь вторым, получим

Или
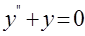 (2).
(2).
Решим полученное линейное уравнение с постоянными коэффициентами (2). Для этого составим характеристическое уравнение и найдем его корни:
λ 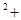 λ=0
λ=0
λ 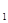 =i
=i
λ  =-i
=-i
Так как характеристическое уравнение имеет два сопряженных корня λ 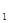 =i и λ
=i и λ 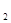 =-i, то общее решение линейного уравнения (2) имеет вид
=-i, то общее решение линейного уравнения (2) имеет вид
y=c 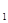 cos t +c
cos t +c  sin t.
sin t.
Подставим значение y в первое уравнение системы (1), получим
z=-c 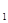 sin t +c
sin t +c  cos t.
cos t.
Тогда общее решение системы (1) имеет вид
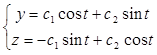 .
.
Составим фундаментальную систему решений системы (1).
Определение1 [2,c.482]. Фундаментальной системой решений в интервале (a,b) называется совокупность n решений однородной системы, определенных и линейно независимых в этом интервале.
Положим c 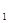 =1,c
=1,c  =0. Подставим значения c
=0. Подставим значения c  и c
и c  в общее решение системы. Получим
в общее решение системы. Получим
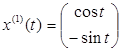 .
.
Пусть теперь c  =0,c
=0,c  =1. Тогда получим
=1. Тогда получим
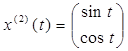 .
.
Эти решения системы (1) запишем в виде матрицы
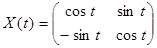 .
.
Покажем, что найденные решения составляют фундаментальную систему решений.
Для этого воспользуемся следующей теоремой.
Теорема 1 [2, c.480]. Если n решений линейной однородной системы линейно независимы в интервале (a,b), то их вронскиан не обращается в нуль ни в одной точке этого интервала. Составим и вычислим вронскиан решений системы (1):
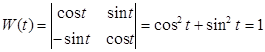 ≠ 0.
≠ 0.
Итак, вронскиан решений системы (1) не обращается в нуль ни в одной точке интервала (−∞; + ∞), значит, найденные решения системы (1) являются линейно независимыми в интервале (−∞; + ∞) (по теореме1) и составляют фундаментальную систему решений (по определению1).
Вычислим характеристические показатели матриц x  и x
и x 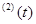 . Приведем определение характеристического показателя.
. Приведем определение характеристического показателя.
Определение2 [1,c.125]. Число (или символ −∞ или + ∞), определяемое формулой
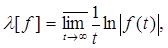
называется характеристическим показателем Ляпунова.
Лемма [1, c.132]. Характеристический показатель конечномерной матрицы F (t) совпадает с характеристическим показателем ее нормы.
Согласно леммы и определения1 характеристические показатели матриц X 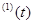 и X
и X  будем вычислять по следующей формуле
будем вычислять по следующей формуле
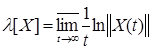 (3).
(3).
Вычислим нормы матриц x  и x
и x 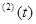 .
.
Определение3 [1,c. 20]. Нормой матрицы А= [a 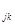 ] называется неотрицательное число
] называется неотрицательное число 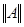 , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
1) 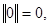 и обратно, если
и обратно, если  то A=0;
то A=0;
2) 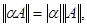 где
где 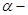 любое комплексное число;
любое комплексное число;
3) 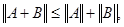 где A,B-любые матрицы, допускающие сложение;
где A,B-любые матрицы, допускающие сложение;
4) 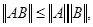 где A,B-любые матрицы, допускающие умножение;
где A,B-любые матрицы, допускающие умножение;
Норма имеет следующие значения:
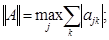
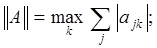
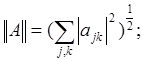
Для вектор-столбца
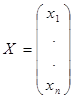
эти нормы имеют соответственно, следующие значения:
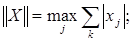

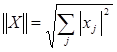 (4).
(4).
При вычислении норм матриц x  и x
и x 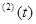 воспользуемся формулой (4).
воспользуемся формулой (4).
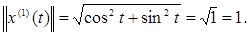
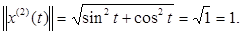
Тогда по формуле (3) имеем
λ 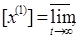

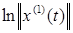 =
= 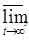

 =
= 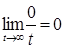 .
.
λ 

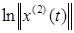 =
= 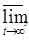

 =
=  .
.