ФИЗИКА
Определение отношения теплоемкости воздуха при постоянном давлении и постоянном объеме
Методические указания
к выполнению лабораторной работы №10
для студентов очной и очно-заочной форм обучения
технических специальностей
Брянск 2010
УДК 530
Физика. Определение отношения теплоемкости воздуха при постоянном давлении и постоянном объеме: методические указания к выполнению лабораторной работы №10 для студентов очной и очно-заочной форм обучения технических специальностей. – Брянск: БГТУ, 2010. – 13 с.
Разработали:
А.А.Демидов,
канд. физ-мат. наук, доц.,
Е.А.Кульченков,
ст. преп.
Рекомендовано кафедрой “Общая физика"
(протокол № 1 от 25.01.10)
Лабораторная работа № 10
Определение отношения теплоемкости воздуха при постоянном давлении и постоянном объеме
Цель лабораторной работы – ознакомление с одним из методов определенияотношения теплоемкости воздуха при постоянном давлении С p к теплоемкости воздуха при постоянном объеме С v.
Оборудование: стеклянный сосуд, манометр, компрессор и секундомер.
Теоретическое введение
Способность любого тела изменять свою температуру при сообщении ему теплоты характеризуется теплоемкостью тела. Применительно к газам наиболее часто используется понятие молярной теплоемкости.
Молярная теплоемкость газа – это величина, численно равная количеству теплоты, необходимому для нагревания 1 моля газа на 1 К
, 
.
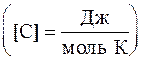Из первого начала термодинамики вытекает, что теплоемкость газов зависит от условий нагревания, т.е. теплоемкость будет различной, если нагревать газ при постоянном объеме (С v) или при постоянном давлении (C p).
Действительно, если газ расширяется изобарически (при P = const), то согласно первому началу термодинамики
Q = D U + A, (1)
количество теплоты Q, полученное газом, расходуется на изменение его внутренней энергии U (U – суммарная, механическая энергия всех молекул газа, [ U ] = Дж) и на совершение работы А ([ А ] = Дж).
Если же процесс изохорический (при V = const), то работа
А = 0 и первый закон термодинамики примет вид:
Q = D U, (2)
т.е. тепло расходуется лишь на изменение внутренней энергии газа.
Если в обоих случаях температура изменилась на 1 К, то изменение внутренней энергии одинаково и из сравнения (1) и (2) очевидно, что при изобарическом процессе теплоемкость больше на величину совершенной работы А, т.е. С p > C v.
Для определения отношения теплоемкости при постоянном давлении С p к теплоемкости при постоянном объеме C v следует рассмотреть процесс, где это отношение играет существенную роль. Таким процессом является адиабатический процесс – процесс, происходящий при отсутствии теплообмена газа с окружающей средой. Адиабатический процесс описывается уравнением Пуассона:
, (3)
либо
. (4)
Здесь Р – давление газа ([ Р ] = Па), V - объем газа ([ V ] = м3)
и 
(5) – показатель адиабаты. Для идеального газа показатель адиабаты будет равен
, (6)
здесь i – количество степеней свободы молекулы рассматриваемого газа, т.е. число координат, необходимое и достаточное для описания положения молекулы в пространстве.
Из выражения (6) видно, что для определения отношения теплоемкостей необходимо вычислить g.
В реальных условиях добиться адиабатического процесса, т.е. осуществить полную теплоизоляцию, очень трудно. На практике пользуются тем фактом, что установление равновесного давления протекает очень быстро – за доли секунды, а на выравнивание температуры вследствие теплообмена газа с внешней средой требуются минуты. Следовательно, для осуществления процесса, близкого к адиабатическому, достаточно быстро изменить давление в газе.
Описание установки и метода измерения
Основным элементом лабораторной установки (рис. 1), позволяющей осуществить процесс, близкий к адиабатическому, необходимый для определения отношения теплоемкости, является стеклянный сосуд, в котором создается с помощью компрессора избыточное давление. Для определения избыточного давления служит U-образный жидкостный (вода) манометр. Расширение находящегося в сосуде газа происходит за счет сообщения сосуда с атмосферой путем нажатия и удержания в течение определенного времени рычага клапана.
Рис. 1. Лабораторная установка
После нагнетания компрессором воздуха в сосуде устанавливается некоторое давление P 1. Так как при сжатии воздух нагревается, то температура воздуха в баллоне после накачивания становится выше комнатной Т 0. Происходит изохорический процесс 0-1 (рис. 2) остывания воздуха при постоянном объеме. При этом давление воздуха в баллоне падает. Этот процесс сопровождается уменьшением разности уровней жидкости в коленах манометра. Стабилизация разности уровней жидкости в коленах манометра указывает на то, что температура воздуха в баллоне достигла комнатной температуры Т 0 (точка 1 на рис. 2). В результате в баллоне устанавливается давление, превышающее атмосферное давление Р 0 на величину Δ P, пропорциональную разности уровней жидкости в коленах манометра. При нажатии на рычаг клапана сосуд сообщается с атмосферой, и воздух адиабатически расширяется (процесс 1-2 на рис. 2). Выражение (4), описывающее этот процесс, сначала прологарифмируем, затем продифференцируем:
. (7)
Поскольку изменение давления и температуры воздуха в сосуде относительно атмосферного невелико, то величины dP и dT можно представить как конечные изменения давления D P и температуры D T:
. (8)
Рис. 2. График изопроцессов, реализующихся в ходе выполнения лабораторной работы
Для адиабаты (1-2) D P = P 0 - P 1; D T = T 1 - T 0. Тогда выражение (8) примет вид:
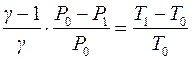. (9)
Как отмечалось, выравнивание давления при открытии сосуда происходит за доли секунды. Клапан же остается открытым в течение более длительного времени. За это время за счет теплообмена воздух будет нагреваться, что приведет к дальнейшему расширению (процесс 2-3 на рис. 2). Расширение будет изобарическим, так как давление остается равным атмосферному.
Количество теплоты dQ, переданное газу при изобарическом расширении, будет равно
,
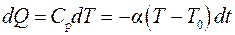где a – коэффициент теплопередачи, зависящий от свойств стенок сосуда, Т – температура воздуха в сосуде, Т 0 – температура среды, окружающей сосуд, т.е. комнатная, dt – время, в течение которого происходит изобарическое расширение газа.
Тогда получаем
. (10)
Так как при изобарическом расширении температура меняется от Т 1 до Т 2, то в результате интегрирования выражения (10) получим
. (11)
После закрытия клапана воздух в сосуде начнет изохорически нагреваться за счет теплообмена через стенки сосуда (процесс 3-4 на рис. 2). Полагая в уравнении Менделеева-Клапейрона
(12)
V = const, прологарифмируем и продифференцируем его,
получим: 
или, если принять конечные величины изменения давления и температуры
. (13)
Для изохоры (3-4) D P = P 2 - P 0, D T = T 0 – T 2, и
. (14)
Разделив уравнение (9) на (14), получим
.
Разность давлений (Р 1 - Р 0) и (Р 2 - Р 0) измеряется жидкостным манометром и поэтому может быть выражена через разность уровней жидкости в коленах манометра D Н (разность уровней жидкости в коленах манометра до открытия клапана) и D h (разность уровней жидкости в коленах манометра через время t после закрытия клапана). С учетом этого
. (15)
Подставим выражение (15) в (11):
. (16)
Из выражения (16) видно, что 
является линейной функцией от времени t. Вид этой функции представлен на рис. 3. Причем, при t = 0
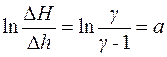. (17)
Из рис. 3 видно, что а – отрезок, отсекаемый при экстраполяции полученной зависимости на оси абсцисс. Из (17) получаем, что
. (18)
Выражение (18) содержит в качестве единственного параметра величину а, которая может быть определена графически. Таким образом, определение отношения теплоемкостей C p и C v сводится к построению графика 
.
Рис. 3. Зависимость
Техника безопаСности
1. Соблюдайте общие правила техники безопасности при использовании электрических приборов.
2. Не загромождайте рабочее место посторонними предметами и будьте аккуратны со стеклянным сосудом.
3. При нажатии кнопки включения компрессора будьте внимательны и не допустите выливания жидкости из манометра.
4. По завершении работы не забудьте отключить секундомер от сети и обесточить всю установку.