Общая постановка задачи
Математическая теория оптимального управления – раздел прикладной математики, в задачах которого процесс управления должен быть непрерывным (не может быть разбит на конечное число этапов).
В качестве управляемой системы S рассматривается некоторый динамический объект (объект, меняющийся во времени). Положение объекта в каждый момент времени 
(состояние системы) полностью характеризуется набором параметров 
. Это могут быть координаты объекта в некоторой системе координат, скорости и т.п.
Определение 10. Вектор 
называют фазовым вектором объекта.
Движением объекта можно управлять с помощью рулей, положение которых в каждый момент времени характеризуется набором параметров
.
Определение 11. Вектор называют управлением.
Предполагается, что состояние объекта в данный момент времени зависит от того, какие значения принимает управление 
до момента времени , и не зависит от будущего поведения управления. Зависимость вектора фазового состояния 
от управления может быть описана системой дифференциальных уравнений
, (35.5)
в которой 
. В этом случае, зная значение управления в каждый момент времени можно определить траекторию объекта как решение системы дифференциальных уравнений 
. Тогда говорят, что задана динамика объекта.
В конкретных задачах управление не может быть произвольным. На него наложены некоторые ограничения, вытекающие из смысла данной задачи. Как правило, предполагают, что вектор управления в каждый момент времени удовлетворяет условию
, (35.6)
где 
– некоторое заданное множество, как правило, замкнутое. Кроме ограничения вида (35.6) могут быть наложены ограничения на зависимость управления от времени (то есть к какому классу функций принадлежит вектор : непрерывных, дифференцируемых, кусочно-непрерывных). В этом случае говорят, что задан класс допустимых управлений .
Предположим, что задан начальный момент времени 
и множество 
допустимых начальных состояний объекта. Требуется так управлять объектом, чтобы в какой-то конечный момент времени 
объект перешел на некоторое множество 
допустимых конечных состояний. Будем считать, что допустимое управление переводит объект из множества начальных состояний 
на множество конечных состояний на отрезке времени 
, если соответствующее этому управлению фазовое состояние объекта удовлетворяет условиям
, 
. (35.7)
Конечный момент времени 
может быть, вообще говоря, не фиксированным, а определяться из условия попадания вектора на конечное множество . Будем предполагать, что допустимые множества и 
заданы.
Может случиться, что управляемый объект можно перевести из множества на множество многими способами. Часто на практике желательно среди всех таких переходов выбрать в каком-то смысле наилучший. Обычно предполагается, что каждому допустимому управлению , заданному на отрезке 
, и соответствующей ему траектории объекта сопоставлено некоторое число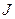 
, оценивающее качество пары , .
Определение 12. Число 
, оценивающее качество пары , называют функционалом или критерием качества.
Например, этот функционал может иметь вид
. (35.8)
Задача оптимального управления: найти такое допустимое управление 
и соответствующее ему траекторию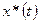 
системы (35.5), переводящую объект из множества (35.6) начальных состояний на множество конечных состояний , что при этом функционал (35.8) принимает экстремальное значение 
. Экстремум находят по всевозможным допустимым управлениям и соответствующим траекториям , переводящим объект из множества начальных состояний на множество конечных состояний .
Пример 35.4. Классическая модель экономического роста. Пусть 
– валовой выпуск в денежном выражении (или национальный доход), полученный на момент времени ; 
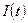– инвестиции в производство на момент времени ; 
– общее потребление на момент времени . Построим модель при следующих основных предположениях.
1. Национальный доход распределяется между потреблением и инвестициями в соответствии с балансовым уравнением 
. Государственные расходы не выделяются.
2. Инвестиции мгновенно поступают в прирост национального дохода (инвестиционный лаг равен нулю) и расходуются только на производство (выбытия денежных средств нет).
3. Расширение производства обеспечивает прирост национального дохода. Скорость роста национального дохода полагается пропорциональной количеству инвестиций: 
(
– капиталоотдача).
4. Экономика считается закрытой (чистый экспорт равен нулю).
5. Затраты труда постоянны во времени или выпуск не зависит от затрат труда, поскольку труд не является дефицитным ресурсом.
6. Научно-технический прогресс не учитывается.
7. Общее потребление 
предполагается заданным экзогенно.
Подставляя 
из балансового уравнения в 
, получаем дифференциальное уравнение классической модели экономического роста
. (35.9)
В отличие от рассмотренных в работах [2], [7], [9]–[12], [15], [39] вариантов модели с постоянным потреблением (
) и потреблением, растущим с постоянным темпом 
(
), можно предположить, что общее потребление является управляющим параметром. Модифицируем модель следующими дополнительными предположениями.
8. Пусть национальный доход образован двумя производственными отраслями: 
, тогда 
, общее потребление в отраслях 
, 
– матрица коэффициентов, характеризующих капиталоотдачу отраслей, 
. Тогда дифференциальное уравнение (35.9) преобразуется в систему дифференциальных уравнений математической модели двухсекторной экономики
Зададим критерий качества. Как правило, в моделях подобного рода критерием качества выступает функция полезности от национального дохода и общего потребления по отраслям: 
(время 
может и не входить явно в функцию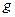 
). Тогда критерий качества представляет собой суммарную полезность от национального дохода и общего потребления по отраслям за период времени от 
до : 
. Очевидно, что суммарная полезность от потребления товаров должна быть максимальной. Например, пусть функция полезности имеет вид функции Р. Стоуна
,
, 
– минимальные уровни потреблений продукции отраслей. Тогда математическая модель оптимального управления двухсекторной экономикой примет вид
Пример 35.5. Неоклассическая модель роста капитала. Неоклассическая модель роста капитала является модификацией классической модели экономического роста. Построим модель при следующих предположениях.
1. Часть национального дохода идет на инвестиции в производство; балансовое уравнение имеет вид 
. Общее потребление не выделяется.
2. Инвестиции мгновенно поступают в прирост национального дохода (инвестиционный лаг равен нулю) и расходуются на расширение производства (увеличение производственных фондов) и амортизацию (ремонт и замену оборудования), то есть 
, где 
– норма амортизации.
4. Экономика считается закрытой (чистый экспорт равен нулю).
5. Валовой выпуск (национальный доход) определяется ценой товара 
и производственной функцией от капитала 
и труда 
: 
.
6. Производственная функция 
является однородной функцией первого порядка, то есть для любого числа 
справедливо равенство 
. В частности, однородными функциями первого порядка являются классическая производственная функция Кобба–Дугласа 
или линейная однородная функция 
.
7. Весь произведенный продукт реализуется полностью (рынок не насыщаем), цена единицы продукта постоянна 
.
8. Научно-технический прогресс не учитывается.
9. Имеет место естественный прирост во времени трудовых ресурсов с постоянным темпом 
(то есть скорость роста ресурса труда пропорциональна количеству ресурса): 
, (где 
– темп изменения числа занятых в производстве).
Подставляя и в , учитывая , получаем систему дифференциальных уравнений, называемую неоклассической моделью роста капитала
Введем управляющий параметр 
, где 
– денежные вливания в экономику извне (например, кредит всемирного банка). Тогда система дифференциальных уравнений примет вид
Зададим критерий качества. Как правило, в экономике критерием качества выступает функция полезности от распределения ресурсов. В рассматриваемой модели функция полезности будет зависеть и от управления: 
. Тогда критерий качества представляет собой суммарную полезность от распределения ресурсов и внешних инвестиций за период времени от до : 
. Очевидно, что суммарная полезность за период времени от до должна быть максимальной. Тогда задача оптимального управления ростом капитала примет вид
Другими словами, задача оптимального управления заключается в нахождении такой допустимой величины внешних инвестиций и соответствующего им распределения ресурсов 
, 
в экономике, что суммарная полезность 
за период времени от до 
должна быть максимальной. Максимум берется по всевозможным допустимым управлениям 
и соответствующим распределениям ресурсов 
и труда .
35.4.2. Основные вопросы математической теории
оптимального управления
1. Управляемость. Решается вопрос: существует ли хотя бы одно допустимое управление , которое переводит динамический объект из множества начальных состояний 
на множество конечных состояний 
, то есть, существует ли такое допустимое управление , при котором соответствующий вектор фазового состояния 
удовлетворяет условиям (35.7). Если этот вопрос решается положительно, то говорят, что объект является управляемым из множества на множество . В противном случае сама постановка задачи оптимального управления теряет смысл.
2. Существование оптимального управления. Пусть существует некоторое управление , которое переводит динамический объект из множества начальных состояний на множество конечных состояний . Необходимо выяснить, существует ли оптимальное управление.
3. Необходимые условия оптимальности. Если оптимальное управление в задаче существует, то далее нужно получить методы нахождения этого оптимального управления. Даже в простых задачах может оказаться бесконечно много допустимых управлений, переводящих динамический объект из множества начальных состояний на множество конечных состояний . Поэтому для нахождения из допустимых управлений оптимального простым перебором всех допустимых управлений обойтись не удается. Возникает вопрос: как сузить класс управлений, подозрительных на оптимальность. Решить его позволяют необходимые условия оптимальности. Таким образом, оптимальное управление нужно искать лишь среди допустимых управлений, удовлетворяющих необходимым условиям оптимальности. Необходимым условием оптимальности является принцип максимума Понтрягина, первоначально высказанный в качестве гипотезы академиком Львом Семеновичем Понтрягиным для управляемых систем, описываемых уравнением вида (35.5), а затем доказанный его учениками. В некоторых задачах может оказаться, что принципу максимума удовлетворяет лишь конечное число управлений, среди которых уже нетрудно выбрать оптимальное.
4. Достаточные условия оптимальности. Во многих задачах, несмотря на то, что необходимые условия оптимальности и позволяют сузить класс управлений, подозрительных на оптимальность, все же этот класс остается достаточно широким. Отобрать действительно оптимальное управление в этом классе позволяют достаточные условия оптимальности. Если некоторое управление из этого класса удовлетворяет достаточным условиям оптимальности, то тем самым гарантируется его оптимальность. Может случиться, что достаточным условиям оптимальности удовлетворяет не одно, а несколько управлений. Тем самым гарантируется, что все они оптимальны, то есть функционал качества принимает на всех этих управлениях одинаковое и притом экстремальное значение.
5. Единственность оптимального управления. Вопрос о том, является ли оптимальное управление единственным, важен с точки зрения приложений теории оптимального управления. Если управление единственно, то в конкретных управляемых объектах практическая реализация единственного оптимального управления может оказаться существенно проще.
Линейная задача быстродействия
Простейшей задачей оптимального управления является линейная задача быстродействия. Динамика объекта в этой задаче будет описываться системой линейных дифференциальных уравнений
, (35.10)
где 
– 
-мерный вектор фазового состояния объекта, 
– -мерный вектор управления, на который наложено ограничение 
, 
– постоянная матрица размерности 
. Начальное и конечное состояния объекта будем выбирать как элементы некоторых непустых и компактных подмножеств и соответственно из -мерного фазового пространства. Критерием качества служит время перехода из множества на множество , то есть 
. Такой критерий качества получается из критерия качества (7.4), когда подынтегральная функция имеет вид 
.
Замечание 1. В математической теории оптимального управления доказано, что линейная задача оптимального быстродействия является управляемой на отрезке времени 
из множества на множество , то есть существует хотя бы одно допустимое управление такое, что соответствующее ему решение переводит объект из множества на множество на отрезке времени .
Замечание 2. В теории обыкновенных дифференциальных уравнений доказано, что линейная система обыкновенных дифференциальных уравнений удовлетворяет условию существования и единственности решения на отрезке 
, то есть, зная некоторую допустимую функцию управления и начальное состояние объекта 
, можно получить единственную функцию 
вектора фазового состояния объекта как решение системы дифференциальных уравнений (35.10).
Замечание 3. В математической теории оптимального управления доказано, что допустимым управлением 
в линейной задаче быстродействия является произвольная измеримая функция, удовлетворяющая включению , где 
является подмножеством 
-мерного координатного пространства. К измеримым функциям относятся, например, постоянные, непрерывные, кусочно-постоянные и кусочно-непрерывные функции.
Линейная задача быстродействия: найти допустимое управление 
и соответствующей ему решения 
системы дифференциальных уравнений (35.10), переводящего объект из множества начальных состояний на множество конечных состояний за минимальное время.
Пример 35.6. Рассмотрим дифференциальное уравнение классической модели экономического роста (см. пример 35.5)
. (35.9)
Линейная задача быстродействия для системы (35.9) формулируется следующим образом: найти допустимое управление 
и соответствующей ему решения 
системы дифференциальных уравнений (35.9), переводящего объект из множества начальных состояний (состояния с данным уровнем экономического развития) на множество конечных состояний (в состояние с желаемым уровнем экономического развития) за минимальное время.
Обозначим 
матрицу, сопряженную матрице . Если матрица 
состоит из вещественных чисел, то 
. Сформулируем необходимое условие оптимальности для линейной задачи быстродействия.
Теорема (принцип максимума Понтрягина). Пусть на отрезке задано некоторое допустимое управление такое, что соответствующее решение системы дифференциальных уравнений (35.10) переводит объект из множества начальных состояний на множество конечных состояний на отрезке времени , то есть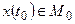 
, 
. Пусть существует такое нетривиальное решение 
вспомогательной системы дифференциальных уравнений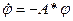 
, что выполнены следующие три условия:
1) 
для почти всех 
;
2) 
;
3) 
.
Тогда пара , удовлетворяет принципу максимума Понтрягина на отрезке времени 
.
Замечание. Для нелинейной системы вида (35.5) можно также сформулировать задачу быстродействия.
Теоретический материал: [2, гл. 29], [6], [10, гл. 7], [12, гл. 29], [22, гл. 8], [26, гл. 3], [30, лекции 1, 6, 9], [39].