При большом числе элементов рисунок графа теряет наглядность. В таком случае его целесообразно задать матричным способом. Граф можно задать различными матрицами, выбор которых обусловлен особенностями конкретной задачи.
Определение 17. Вершины  и
и  графа называют смежными, если они соединены дугой (ребром).
графа называют смежными, если они соединены дугой (ребром).
Определение 18. Матрицей смежности вершин  орграфа называют квадратную матрицу
орграфа называют квадратную матрицу  -го порядка, в которой
-го порядка, в которой  – число вершин графа; строки и столбцы матрицы соответствуют вершинам графа; элементы
– число вершин графа; строки и столбцы матрицы соответствуют вершинам графа; элементы  матрицы равны числу дуг, направленных из вершины
матрицы равны числу дуг, направленных из вершины  в вершину
в вершину  .
.
Замечание. Если орграф состоит из однократных дуг, то элементы его матрицы смежности вершин равны либо 0, либо 1. В случае неориентированного графа ему вместе с ребром  принадлежит и ребро
принадлежит и ребро  , поэтому матрица неориентированного графа будет симметрической (то есть ее элементы, симметричные относительно главной диагонали, равны). Справедливо и обратное утверждение: любой симметрической матрице с целыми неотрицательными элементами можно поставить в соответствие неориентированный граф.
, поэтому матрица неориентированного графа будет симметрической (то есть ее элементы, симметричные относительно главной диагонали, равны). Справедливо и обратное утверждение: любой симметрической матрице с целыми неотрицательными элементами можно поставить в соответствие неориентированный граф.
Определение 19. Дуги  и
и  называют смежными, если дуга
называют смежными, если дуга  входит в вершину
входит в вершину  , а дуга
, а дуга  выходит из нее.
выходит из нее.
Определение 20. Матрицей смежности дуг 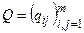 орграфа называют квадратную матрицу
орграфа называют квадратную матрицу  -го порядка, в которой
-го порядка, в которой  – число дуг графа; строки и столбцы матрицы соответствуют дугам графа; элементы
– число дуг графа; строки и столбцы матрицы соответствуют дугам графа; элементы  матрицы равны 1, если дуга
матрицы равны 1, если дуга  непосредственно предшествует дуге
непосредственно предшествует дуге  , и 0 в остальных случаях.
, и 0 в остальных случаях.
Определение 21. Ребра  и
и  называют смежными, если они имеют общую вершину.
называют смежными, если они имеют общую вершину.
Определение 22. Матрицей смежности ребер  неориентированного графа называют квадратную матрицу
неориентированного графа называют квадратную матрицу  -го порядка, в которой
-го порядка, в которой  – число ребер графа; строки и столбцы матрицы соответствуют ребрам графа; элементы
– число ребер графа; строки и столбцы матрицы соответствуют ребрам графа; элементы  матрицы равны 1, если ребра
матрицы равны 1, если ребра  и
и  имеют общую вершину, и 0 в остальных случаях.
имеют общую вершину, и 0 в остальных случаях.
Замечание. Матрица смежности ребер графа является симметрической.
Определение 23. Дугу  и вершину
и вершину  называют инцидентными, если вершина
называют инцидентными, если вершина  является началом или концом дуги
является началом или концом дуги  .
.
Определение 24. Ребро  и вершину
и вершину  называют инцидентными, если инцидентны вершина
называют инцидентными, если инцидентны вершина  и дуга
и дуга  (другими словами, вершина
(другими словами, вершина  является началом или концом ребра
является началом или концом ребра  ).
).
Определение 25. Матрицей инцидентности  орграфа называют прямоугольную матрицу размерности
орграфа называют прямоугольную матрицу размерности  , строки которой соответствуют вершинам, а столбцы – дугам орграфа, причем
, строки которой соответствуют вершинам, а столбцы – дугам орграфа, причем

Замечание. В случае неориентированного графа элементами матрицы инцидентности будут только числа 0 и 1.
Таким образом, всякий граф можно задать одной из матриц смежности или матрицей инцидентности.
 Пример 36.3. Для графа, изображенного на рис 36.5, найти матрицу смежности вершин, матрицу смежности дуг и матрицу инцидентности.
Пример 36.3. Для графа, изображенного на рис 36.5, найти матрицу смежности вершин, матрицу смежности дуг и матрицу инцидентности.
Решение. Найдем матрицу смежности вершин.Граф, изображенный на рис 36.5, содержит четыре вершины, поэтому матрица смежности его вершин  будет четвертого порядка (
будет четвертого порядка ( ). На основании определений 17 и 18 найдем значения элементов матрицы
). На основании определений 17 и 18 найдем значения элементов матрицы  . Граф является орграфом и состоит из однократных дуг. Смежными являются вершины
. Граф является орграфом и состоит из однократных дуг. Смежными являются вершины  и
и  ,
,  и
и  ,
,  и
и  ,
,  и
и  ,
,  и
и  ,
,  и
и  (так как у вершины
(так как у вершины  есть петля). Поэтому элементы матрицы смежности вершин
есть петля). Поэтому элементы матрицы смежности вершин  ,
,  ,
,  ,
,  ,
,  и
и  равны единице, а остальные – нулю.
равны единице, а остальные – нулю.
Вычисления удобно проводить с помощью таблицы, у которой строки и столбцы выделенной части заполняют следующим образом: если вершины  и
и  являются смежными (соединены хотя бы одной дугой), то на пересечении строки
являются смежными (соединены хотя бы одной дугой), то на пересечении строки  и столбца
и столбца  пишут количество дуг, соединяющих вершины
пишут количество дуг, соединяющих вершины  и
и  (элемент
(элемент  ); если же вершины
); если же вершины  и
и  не являются смежными (не соединены ни одной дугой), то
не являются смежными (не соединены ни одной дугой), то  .
.

| 
| 
| 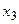
| 
|

| ||||

| ||||
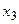
| ||||

|
Выделенная часть таблицы представляет собой матрицу смежности вершин орграфа. Таким образом, матрица смежности вершин графа имеет вид
 .
.
Найдем матрицу смежности вершин.Всего в данном графе шесть дуг, поэтому матрица смежности дуг  орграфа будет порядка
орграфа будет порядка  . Согласно определениям 19 и 20 перечислим смежные дуги и определим элементы
. Согласно определениям 19 и 20 перечислим смежные дуги и определим элементы  . Смежными дугами при вершине
. Смежными дугами при вершине 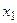 являются дуги
являются дуги  и
и  (
( входит в вершину
входит в вершину 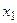 , а
, а  выходит из нее), поэтому
выходит из нее), поэтому 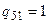 ; а также – дуги
; а также – дуги  и
и  , поэтому
, поэтому 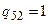 . Смежными дугами при вершине
. Смежными дугами при вершине  являются дуги
являются дуги  и
и  , поэтому
, поэтому  ; а также – дуги
; а также – дуги  и
и  , поэтому
, поэтому  . Смежными дугами при вершине
. Смежными дугами при вершине 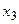 являются дуги
являются дуги  и
и  , поэтому
, поэтому  ; а также – дуги
; а также – дуги  и
и  , поэтому
, поэтому  . Смежными дугами при вершине
. Смежными дугами при вершине  являются дуги
являются дуги  и
и  , поэтому
, поэтому  ; а дуга
; а дуга  является смежной сама себе, поэтому
является смежной сама себе, поэтому  . Остальные элементы равны нулю.
. Остальные элементы равны нулю.
Вычисления элементов матрицы  удобно выполнять в виде таблицы. Таблицу заполняют следующим образом: если две дуги
удобно выполнять в виде таблицы. Таблицу заполняют следующим образом: если две дуги  и
и  являются смежными при некоторой вершине
являются смежными при некоторой вершине  , то на пересечении строки
, то на пересечении строки  и
и  (элемент
(элемент  ) пишут единицу; в противном случае – 0.
) пишут единицу; в противном случае – 0.

| 
| 
| 
| 
| 
| 
| Выделенная часть таблицы представляет собой матрицу смежности дуг графа. Тогда 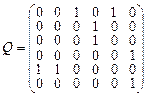 . .
|

| |||||||

| |||||||

| |||||||

| |||||||

| |||||||

|
Найдем матрицу инцидентности графа. Граф состоит из четырех вершин и шести дуг, поэтому его матрица инцидентности будет иметь размерность 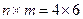 . Для вычисления ее элементов заполним вспомогательную таблицу согласно определениям 23 и 25: если дуга
. Для вычисления ее элементов заполним вспомогательную таблицу согласно определениям 23 и 25: если дуга  заходит в вершину
заходит в вершину  , то на пересечении строки
, то на пересечении строки  и столбца
и столбца  ставим (–1), элемент
ставим (–1), элемент  ; если дуга
; если дуга  исходит из вершины
исходит из вершины  , то на пересечении строки
, то на пересечении строки  и столбца
и столбца  ставим 1, элемент
ставим 1, элемент  ; если дуга
; если дуга  и вершина
и вершина  никак не связаны, то
никак не связаны, то  .
.
Например, дуга 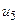 входит в вершину
входит в вершину 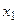 , поэтому
, поэтому 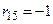 .
.


| 
| 
| 
| 
| 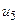
| 
|
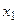
| –1 | |||||

| –1 | |||||
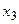
| –1 | –1 | ||||

| –1; 1 |
Выделенная часть таблицы представляет собой матрицу инцидентности графа. Тогда матрица инцидентности имеет вид  .
.
Ответ. Матрица смежности вершин  , матрица смежности дуг
, матрица смежности дуг  , матрица инцидентности
, матрица инцидентности  .
.
Пример 36.4. По заданной матрице смежности вершин  построить наглядное изображение графа.
построить наглядное изображение графа.
Решение. Матрица смежности вершин графа не является симметрической и не содержит симметрических подматриц, следовательно, данный граф является орграфом (полностью ориентированным). Составим вспомогательную таблицу:

| 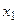
| 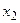
| 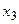
|
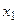
| |||
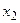
| |||
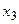
|
Так как матрица  является матрицей смежности вершин и имеет размерность
является матрицей смежности вершин и имеет размерность  , то граф имеет три вершины. Найдем направления дуг. Так как
, то граф имеет три вершины. Найдем направления дуг. Так как  , то вершина
, то вершина  не является смежной сама себе, то есть граф не имеет петли в этой вершине. Так как
не является смежной сама себе, то есть граф не имеет петли в этой вершине. Так как  , то вершину
, то вершину  с вершиной
с вершиной  соединяют две дуги. Так как
соединяют две дуги. Так как  , то вершину
, то вершину  с вершиной
с вершиной 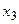 соединяет одна дуга. Так как
соединяет одна дуга. Так как  , то вершину
, то вершину 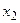 с вершиной
с вершиной  соединяет одна дуга. Так как
соединяет одна дуга. Так как  ,
,  то вершина
то вершина  является смежной сама себе. Следовательно, граф имеет петлю у вершины
является смежной сама себе. Следовательно, граф имеет петлю у вершины  . Так как
. Так как  , то вершину
, то вершину 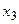 с вершиной
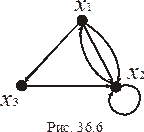
с вершиной 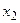 соединяет одна дуга. Остальные элементы третьей строки равны нулю, то есть других соединений нет. Расположим на плоскости вершины графа и соединим их стрелками, имеющими соответствующие направления. Получим искомый орграф (рис. 36.6).
соединяет одна дуга. Остальные элементы третьей строки равны нулю, то есть других соединений нет. Расположим на плоскости вершины графа и соединим их стрелками, имеющими соответствующие направления. Получим искомый орграф (рис. 36.6).