1. В таблице указан возможный прирост выпуска продукции четырьмя плодово-консервными заводами области в млн руб. при осуществлении инвестиций на их модернизацию с дискретностью в 50 млн руб., причем на один завод можно осуществить только одну инвестицию. Составить план распределения инвестиций между заводами области, максимизирующий общий прирост выпуска продукции.
| Выделяемые средства, млн руб. | Прирост выпуска продукции, млн руб. | |||
| Предприятие № 1 | Предприятие № 2 | Предприятие № 3 | Предприятие № 4 | |
2. Разработать оптимальную стратегию использования и замены оборудования не старше  лет, если для каждого года планового периода известны стоимость продукции
лет, если для каждого года планового периода известны стоимость продукции  , производимой с использованием этого оборудования, и эксплуатационные расходы
, производимой с использованием этого оборудования, и эксплуатационные расходы  . Известны также остаточная стоимость
. Известны также остаточная стоимость  и цена нового оборудования
и цена нового оборудования 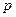 , не меняющаяся в плановом периоде. Продолжительность планового периода принять равной
, не меняющаяся в плановом периоде. Продолжительность планового периода принять равной  годам. Задачу решить при следующих числовых данных:
годам. Задачу решить при следующих числовых данных:  =6,
=6,  =2,
=2, 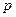 =10, значения
=10, значения 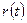 и
и  см. в таблице,
см. в таблице,  = 6,
= 6,  = 4.
= 4.

| |||||||
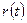
| |||||||

|
3. Производственное объединение выделяет входящим в него четырем предприятиям средства в объеме 60 млн руб. для расширения производства и увеличения выпуска продукции. Выделяемые предприятиям суммы кратны 20 млн руб. По каждому предприятию известен возможный прирост выпуска продукции (в денежном выражении) в зависимости от выделенной ему суммы.
| Выделяемые средства, млн руб. | Прирост выпуска продукции, млн руб. | |||
| Предприятие № 1 | Предприятие № 2 | Предприятие № 3 | Предприятие № 4 | |
Предполагается, что прирост выпуска продукции на  -м предприятии не зависит от суммы средств, вложенных в другие предприятия, а общий прирост выпуска продукции в производственном объединении равен сумме приростов, полученных на каждом предприятии объединения. Требуется так распределить средства между предприятиями, чтобы общий прирост выпуска продукции на производственном объединении был максимальным.
-м предприятии не зависит от суммы средств, вложенных в другие предприятия, а общий прирост выпуска продукции в производственном объединении равен сумме приростов, полученных на каждом предприятии объединения. Требуется так распределить средства между предприятиями, чтобы общий прирост выпуска продукции на производственном объединении был максимальным.
Тема 36. Элементы теории графов
Способы задания графов
Пусть дано некоторое множество  и множество отношений
и множество отношений  , устанавливающих соответствие между каждым элементом множества
, устанавливающих соответствие между каждым элементом множества  и некоторым подмножеством множества
и некоторым подмножеством множества  .
.
Определение 1. Графом называют упорядоченную пару объектов 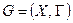 .
.
Определение 2. Граф называют конечным, если множество  – конечное.
– конечное.
Определение 3. Элементы множества  называют вершинами графа и обозначают
называют вершинами графа и обозначают  ,
, 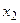 , …,
, …,  .
.
Определение 4. Отношение, устанавливающее соответствие между вершинами графа 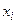 и
и  в направлении от
в направлении от 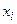 к
к  , называют дугой.
, называют дугой.
Определение 5. Множество  называют множеством дуг графа.
называют множеством дуг графа.
Замечание. В виде графа можно изобразить сеть улиц в городе: вершины графа – перекрестки, дуги – улицы с разрешенным направлением движения (улицы могут быть с односторонним и двусторонним движением). В виде графа можно изобразить схему железных дорог или метро: вершины графа – станции, дуги – перегоны между ними (две вершины графа могут быть соединены несколькими дугами, идущими в одном направлении). В виде графа можно представить диаграмму причинно-следственной информации: вершины – основные факторы, дуги – взаимосвязи или влияние факторов.
Определение 6. Отношение, устанавливающее соответствие между вершинами графа 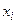 и
и  без указания направления, называют ребром.
без указания направления, называют ребром.
Замечание. Ребром графа также называют пару дуг, устанавливающих соответствие между вершинами графа  и
и  в направлении от
в направлении от  к
к  и в направлении от
и в направлении от  к
к  .
.
Определение 7. Граф, состоящий только из дуг, называют ориентированным графом (орграфом).
Определение 8. Граф, состоящий только из ребер, называют неориентированным (полностью неориентированным) графом.
Определение 9. Граф, состоящий из дуг и ребер, называют смешанным графом.
Определение 10. Дугу графа, у которой начальная и конечная вершины совпадают, называют петлей.
Определение 11. Дуги графа называют кратными, если они соединяют две заданных вершины графа и идут в одном направлении.
Определение 12. Граф, содержащий кратные дуги, называют мультиграфом.
Определение 13. Полностью неориентированный граф (орграф) называют полным, если любые две его вершины соединены одним и только одним ребром (дугой).
Замечание. В полном графе каждая вершина принадлежит одному и тому же числу ребер, так как она соединена со всеми остальными вершинами. Для задания полного графа достаточно знать число его вершин.
Существуют аналитический, графический и матричные способы задания графа.