I уровень
1.1. Укажите, какие предложения определяют высказывание:
1) Пусть всегда будет солнце!
2) Минск – столица Болгарии.
3) Число 7 больше числа 5.
4) Ты идешь сегодня в школу.
5) Выражение  принимает значения больше нуля или равно нулю.
принимает значения больше нуля или равно нулю.
1.2. Среди приведенных высказываний назовите простые и сложные:
1) Если сумма углов четырехугольника равна 3600, то четырехугольник является квадратом.
2) Квадрат является ромбом.
3) Треугольник является равносторонним тогда и только тогда, когда сумма двух его сторон больше третьей стороны.
4) Если высота треугольника проведена к основанию и она является медианой, то треугольник – равнобедренный.
5) Число 15 делится нацело на 7.
6) Если в четырехугольнике стороны попарно параллельны или попарно равны, то такой четырехугольник является параллелограммом.
1.3. Даны высказывания:
А: Развернутый угол равен 1800.
В: Число 7 является четным.
С: Беларусь – европейская страна.
D: Минск – столица Беларуси.
Сформулируйте высказывания: 
1.4. Определите тип теоремы:
1) Четырехугольник является параллелограммом тогда и только тогда, когда две его противоположные стороны параллельны и равны.
2) Если  корни квадратного трехчлена
корни квадратного трехчлена  , то
, то  .
.
3) Числа 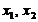 являются корнями квадратного трехчлена
являются корнями квадратного трехчлена  тогда и только тогда, когда
тогда и только тогда, когда

4) Если окружность вписана в четырехугольник, то суммы противоположных сторон равны.
5) Для того, чтобы окружность была вписана в четырехугольник, необходимо и достаточно, чтобы суммы противоположных сторон были равны.
1.5. Для теоремы «Если треугольник прямоугольный, то сумма квадратов катетов равна квадрату гипотенузы» сформулируйте:
1) обратную;
2) противоположную;
3) противоположную к обратной;
4) необходимые и достаточные условия.
Определите значение И или Л сформулированных утверждений.
1.6. Докажите справедливость равенств для всех n Î N:
1) 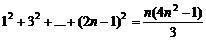 ;
;
2)  ;
;
3)  .
.
II уровень
Введите обозначения буквами всех простых высказываний, приведенных в примере 1.2. Запишите символически сложные высказывания с помощью операций над высказываниями. Определите их значение (И или Л).
Установите, равны ли по значению пары высказываний:
1) 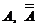 ; 2)
; 2)  ; 3)
; 3) 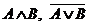 .
.
Приведите пример конкретных математических высказываний A, B, C, которые соответствовали бы содержательно высказываниям:
1)  ; 2)
; 2)  .
.
Докажите, что сумма первых n чисел натурального ряда равна  .
.
Докажите, что для всех n, n Î N верно равенство:
1) 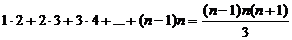 ;
;
2)  ;
;
3)  .
.
Докажите неравенство:
1)  , если n Î N;
, если n Î N;
2)  , если n Î N, n ³ 5.
, если n Î N, n ³ 5.
III уровень
3.1. Докажите, что высказывания  равны при всех возможных значениях высказываний A, B.
равны при всех возможных значениях высказываний A, B.
3.2. На вопрос, кто из трех студентов сдал экзамен на «отлично» был получен правдивый ответ: «когда сдал первый, то сдал и третий, но неправда, что если сдал второй, то сдал и третий». Определите, какой студент сдал экзамен на «отлично».
3.3. Выясните истинность высказывания:
1)  , если В и С истины;
, если В и С истины;
2)  , если A, B – ложны, C – истинно.
, если A, B – ложны, C – истинно.
3.4. Докажите, что при всех n Î N выполняется:
1)  кратно 3;
кратно 3;
2)  кратно 7.
кратно 7.
3)  кратно 19;
кратно 19;
4) 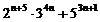 кратно 37.
кратно 37.
3.5. Докажите, что
1)  кратно 8, если
кратно 8, если  нечетное;
нечетное;
2)  кратно 8, если
кратно 8, если  четное.
четное.