Высказывания. Типы теорем. Метод математической индукции

Введение

 

Под простым высказыванием понимают утверждение (повествовательное предложение), в отношении которого можно сказать, истинно оно или ложно (но не то и другое вместе).

Высказывания обозначают латинскими буквами A, B, C, …, их значения истина и ложь соответственно, через «И» и «Л». Сложные высказывания получают из простых при помощи логических операций, к которым относятся отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность (эквиваленция).

 

Если А — высказывание, то отрицание высказывания А определяется как такое высказывание, которое истинно тогда и только тогда, когда высказывание А ложно. Отрицание высказывания А обозначается 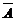(или Ø А) и читается «не А».

Истинность-ложность операции отрицания выражает истинностная таблица1.

Таблица 1.

А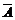
И	Л
Л	И

Конъюнкцией двух высказываний называется такое высказывание, которое истинно тогда и только тогда, когда оба составляющие ее высказывания истинны.

Если А, В - высказывания, то их конъюнкция обозначается A Ù B (или А & B) и читается «А и В».

Конъюнкции соответствует истинностная таблица 2.

Таблица 2

А	В	А Ù В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Дизъюнкцией двух высказываний называется такое высказывание, которое ложно тогда и только тогда, когда оба составляющие ее высказывания ложны.

Если А, В - два высказывания, то их дизъюнкция обозначается А Ú В и читается «А или В». Союз «или» здесь употребляется в соединительном, а не в разделительном смысле, то есть для истинности высказывания А Ú В допускается также случай истинности обоих высказываний А, В.

Операции дизъюнкции соответствует истинностная таблица 3.

Таблица 3

А	В	А Ú В
И	И	И
Л	И	И
И	Л	И
Л	Л	Л

Импликация высказываний А, В определяется как такое высказывание, которое ложно тогда и только тогда, когда высказывание А истинно, а высказывание В ложно. Импликация двух высказываний А, В обозначается АÞВ и читается «если А, то В». Высказывание А называется посылкой импликации, а В - заключением.

Импликации соответствует истинностная таблица 4.

Таблица 4.

А	В	А Þ В
И	И	И
Л	И	И
И	Л	Л
Л	Л	И

Эквивалентность двух высказываний А, В определяется как высказывание, которое истинно тогда и только тогда, когда высказывания А, В оба истинны или оба ложны. Обозначается АÛВ и читается «А тогда и только тогда, когда В» («если А, то В, и, если В, то А», «А есть необходимое и достаточное условие для В»). Значения эквивалентности определены в истинностной таблице 5.

Таблица 5.

А	В	А Û В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Если теорема сформулирована в виде A Þ B, то она называется признаком или достаточным условием для B, где A, B –некоторые высказывания.

Теорема типа В Þ А называется обратной для теоремы A Þ B.

Если теорема имеет вид A Û B, то она называется критерием или необходимым и достаточным условиями для B.

Теорема такого типа объединяет прямую и обратную теоремы.

Теорема типа 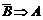называется противоположной к обратной теореме.

Высказывание A Þ B истинно тогда и только тогда, когда истинно высказывание 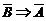. На этом факте основан метод доказательства от противного.

 

Для доказательства истинности некоторого утверждения А(n) при всех значениях натуральной переменной n, от которой оно зависит (начиная с n₀, n₀ Î N), часто используют метод математической индукции. Для этого необходимо сделать следующие три шага:

1) непосредственной проверкой убедиться в истинности А(n₀);

2) допустить, что А(k) истинно для любого k ³ n₀;

3) доказать, что А(k+ 1 ) истинно для всех k Î N, k ³ n₀.

 

Пример 1. Заданы высказывания:

А: Число 7 больше числа 6;

В: Число 7 равно числу 6;

С: сумма углов треугольника равна 180⁰.

Рассмотреть следующие высказывания и установить их значения (И или Л): 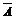, , 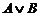, 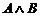A Þ B, B Û C, ,

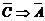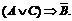
Решение. 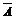: число 7 не больше числа 6. Это высказывание если Л, т.к. А – И.

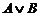: число 7 больше или равно числу 6. Это высказывание является дизъюнкцией высказываний А, В, где А – И, В – Л. Согласно таблице 3, оно есть И.

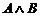: число 7 больше и равно числу 6. Это конъюнкция высказываний, где А – И, В – Л. По таблице 2 оно есть Л.

A Þ C: если число 7 больше числа 6, то сумма углов треугольника равна 180⁰. Это импликация двух истинных высказываний, а поэтому оно есть И.

B Û C: число 7 равно числу 6 тогда и только тогда, когда сумма углов треугольника равна 180⁰. Поскольку В – Л, С – И, то согласно таблице 5 для эквивалентности получаем, что B Û C если Л.

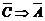: если сумма углов треугольника не равна 180⁰, то число 7 не больше числа 6. Поскольку рассматривается импликация двух ложных высказываний, то по таблице 4 это высказывание есть И.

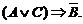: если число 7 больше 6 или сумма углов треугольника равна 180⁰, то число 7 не равно числу 6. Высказывание 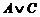является И (по таблице 3 как дизъюнкция двух истинных высказываний). Высказывание 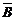также есть И. Тогда рассматриваемая импликация по своему значению есть И.

Пример 2. Доказать истинность эквивалентности

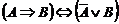(1)

Решение. Для доказательства рассмотрим четыре возможных случая.

1. Пусть обо высказывания A, B есть истина. Тогда согласно таблице 4 истинности для импликации, A Þ B есть И. Поскольку B есть И, то по таблице истинности 3 для дизъюнкции 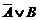есть И. Значит, высказывания в левой и правой частях истинны, значит, эквивалентность также есть И.

2. Пусть A является истиной, B – ложное. Тогда импликация A Þ B есть Л. В правой части эквивалентности (1) также имеем ложное высказывание, т.к. это дизъюнкция двух ложных высказываний. Значит, эквивалентность (1) является истиной.

3. Пусть A есть ложь, B – истина. Тогда A Þ B есть И, 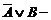И, а поэтому эквивалентность (1) является истинной.

4. Пусть оба высказывания A, B есть Л. Тогда A Þ B есть 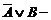И, И.

Мы доказали, что во всех возможных случаях исходных значений высказываний A, B эквивалентность (1) есть И.

Пример 3: Доказать справедливость формулы

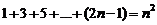(2)

для любого n Î N.

Решение: Используем метод математической индукции.

1. Проверяем справедливость равенства (2) при n =1. Для этого в равенстве (2) полагаем n =1, причем левая часть равенства будет состоять из одного слагаемого:

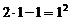, 1=1 – выполняется.

2. Допускаем,что для n = k верно утверждение

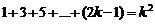(3)

3. Доказываем его истинность для n = k + 1:

Рассмотрим левую часть равенства (2):

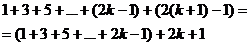
Используем далее тот факт, что выражение в последних скобках, согласно (3), равно 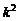. В итоге получаем

.

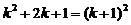Правая часть равенства (2) для k + 1 имеет вид: .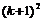

Очевидно, что левая и правая части равенства (3) при n = k + 1 равны.

Т.к. все три шага математической индукции реализованы, формула верна для любого n Î N.

Пример 4. Найти все натуральные числа n, для которых верно неравенство

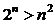. (4)

Решение: Утверждение, которое можно было бы доказывать методом математической индукции явно не сформулировано. По этой причине выясним закономерность взаимозависимости величин 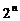и 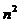. Придадим последовательно числу n значения 1, 2, 3, 4, 5, 6 и соответственно получим 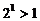, , 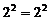, , 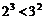, 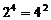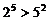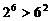. Таким образом, можно высказать гипотезу: исходное неравенство справедливо для n = 1 и каждого натурального n 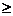5. Докажем это утверждение.

1. Истинность неравенства (4) для n = 5 уже доказана.

2. Допустим, что неравенство (4) верно для любого n = k, k ³ 5, k Î N, т.е.

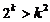. (5)

Используя неравенство (5), докажем неравенство

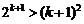. (6)

Исходя из неравенства (5) имеем

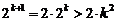. (7)

Заметим, что 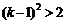для всех натуральных k ³ 3, в чем можно убедиться, например, графически (см. рис.1)

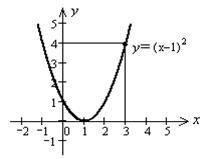
Рис.1

 

Тогда 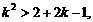или 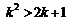. Прибавим к обеим частям последнего неравенства 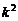. Получим .

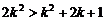Полученное неравенство может быть записано в виде 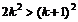. Вместе с неравенством (7) оно доказывает справедливость неравенства (6).

На основании метода математической индукции приходим к выводу, что исходное неравенство верно для каждого k ³ 5, и, кроме этого, непосредственно убедились, что верно и для n = 1.